人教版 初三数学 24.1 圆的有关性质 同步课时训练(word含答案)
文档属性
| 名称 | 人教版 初三数学 24.1 圆的有关性质 同步课时训练(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 15:45:23 | ||
图片预览



文档简介
人教版
初三数学
24.1
圆的有关性质
同步课时训练
一、选择题
1.
已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
A.45°
B.35°
C.25°
D.20°
2.
小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是
( )
A.AB,AC边上的中线的交点
B.AB,AC边上的垂直平分线的交点
C.AB,AC边上的高所在直线的交点
D.∠BAC与∠ABC的角平分线的交点
3.
如图,在直角坐标系中,以原点为圆心,半径为5的圆内有一点P(0,-3),那么经过点P的所有弦中,最短的弦的长为( )
A.4
B.5
C.8
D.10
4.
如图,著名水乡乌镇的一圆拱桥的拱顶到水面的距离CD为8
m,水面宽AB为8
m,则拱桥的半径OC为( )
A.4
m
B.5
m
C.6
m
D.8
m
5.
如图,AD是⊙O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB相交于点P,下列结论错误的是( )
A.AP=2OP
B.CD=2OP
C.OB⊥AC
D.AC平分OB
6.
2019·聊城
如图,BC是半圆O的直径,D,E是上的两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为( )
A.35°
B.38°
C.40°
D.42°
7.
如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
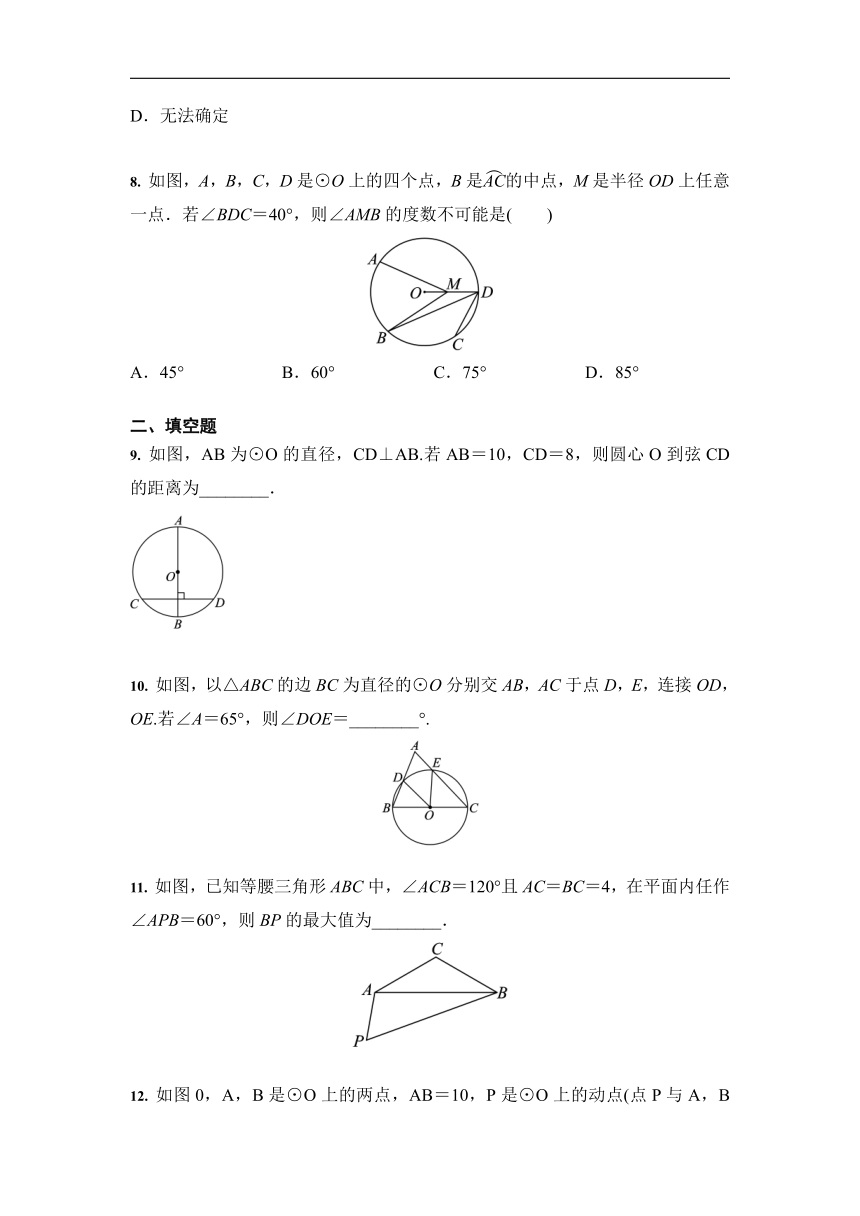
8.
如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
A.45°
B.60°
C.75°
D.85°
二、填空题
9.
如图,AB为⊙O的直径,CD⊥AB.若AB=10,CD=8,则圆心O到弦CD的距离为________.
10.
如图,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE.若∠A=65°,则∠DOE=________°.
11.
如图,已知等腰三角形ABC中,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,则BP的最大值为________.
12.
如图0,A,B是⊙O上的两点,AB=10,P是⊙O上的动点(点P与A,B两点不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=________.
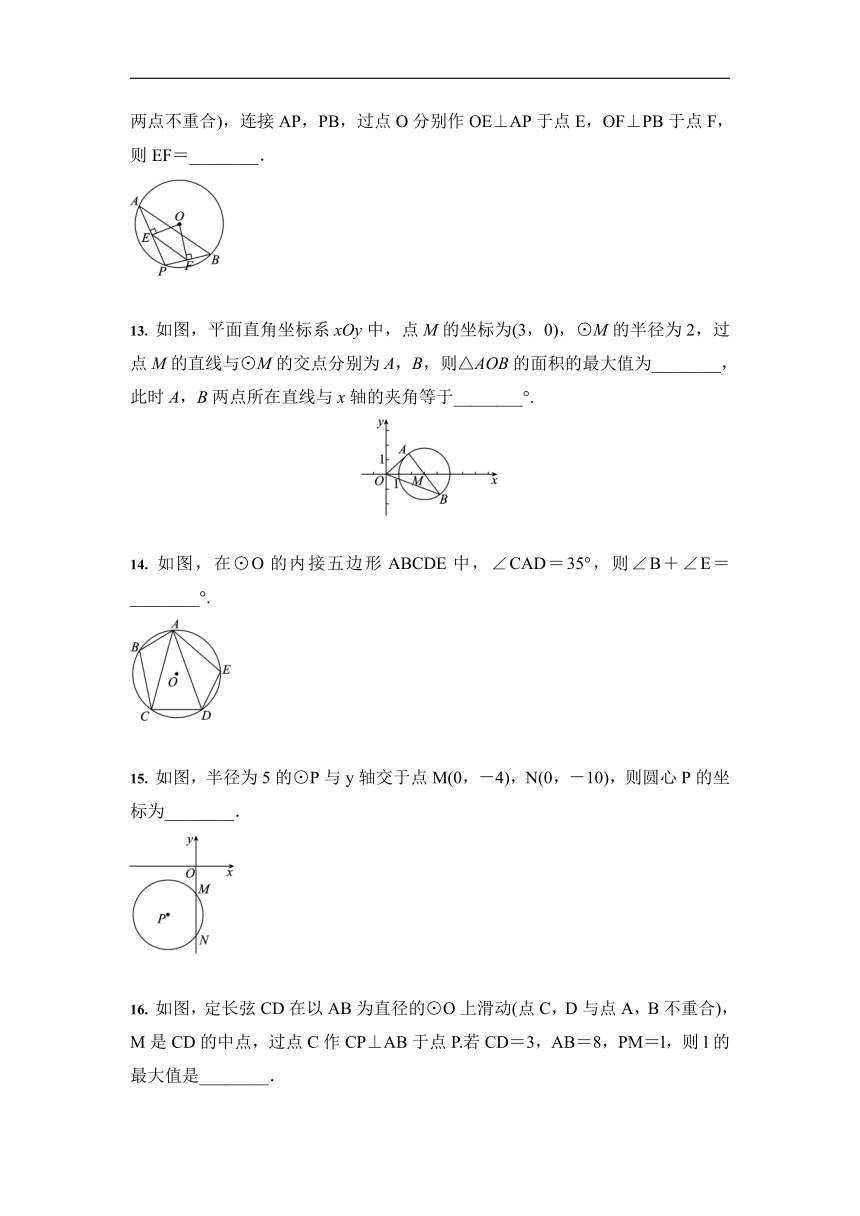
13.
如图,平面直角坐标系xOy中,点M的坐标为(3,0),⊙M的半径为2,过点M的直线与⊙M的交点分别为A,B,则△AOB的面积的最大值为________,此时A,B两点所在直线与x轴的夹角等于________°.
14.
如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=________°.
15.
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),则圆心P的坐标为________.
16.
如图,定长弦CD在以AB为直径的⊙O上滑动(点C,D与点A,B不重合),M是CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=8,PM=l,则l的最大值是________.
三、解答题
17.
如图所示,AB,CD是⊙O的两条直径,弦BE=BD.求证:=.
18.
已知:如图5,在⊙O中,M,N分别为弦AB,CD的中点,AB=CD,AB不平行于CD.
求证:∠AMN=∠CNM.
19.
如图,点E是△ABC的内心,线段AE的延长线交BC于点F(∠AFC≠90°),交△ABC的外接圆于点D.
(1)求点F与△ABC的内切圆⊙E的位置关系;
(2)求证:ED=BD;
(3)若∠BAC=90°,△ABC的外接圆的直径是6,求BD的长;
(4)B,C,E三点可以确定一个圆吗?若可以,则它们确定的圆的圆心和半径分别是什么?若不可以,请说明理由.
20.
如图,四边形OBCD中的三个顶点在⊙O上,A是优弧BAD上的一个动点(不与点B,D重合).
(1)当圆心O在∠BAD的内部时,若∠BOD=120°,则∠OBA+∠ODA=________°.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.
人教版
初三数学
24.1
圆的有关性质
同步课时训练-答案
一、选择题
1.
【答案】A
2.
【答案】B [解析]本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点,故选B.
3.
【答案】C [解析]
过点P作弦AB⊥OP,连接OB,如图.
则PB=AP,∴AB=2BP=2
.
再过点P任作一条弦MN,过点O作OG⊥MN于点G,连接ON.
则MN=2GN=2
.
∵OP>OG,OB=ON,∴MN>AB,
∴AB是⊙O中的过点P最短的弦.
在Rt△OPB中,PO=3,OB=5,由勾股定理,得PB=4,则AB=2PB=8.
4.
【答案】B [解析]
如图,连接BO.
由题意可得AD=BD=4
m.
设⊙O的半径OC=x
m,则DO=(8-x)m.
由勾股定理可得x2=(8-x)2+42,解得x=5.
故拱桥的半径OC为5
m.
5.
【答案】A [解析]
∵AD是⊙O的直径,
∴∠ACD=90°.
∵四边形OBCD是平行四边形,
∴CD∥OB,CD=OB,∴∠CPO=90°,
即OB⊥AC,∴选项C正确;
∴CP=AP.又∵OA=OD,
∴OP是△ACD的中位线,
∴CD=2OP,∴选项B正确;
∴CD=OB=2OP,即P是OB的中点,
∴AC平分OB,∴选项D正确.
6.
【答案】C
7.
【答案】C
8.
【答案】D [解析]
连接AD,OA,OB.∵B是的中点,∴∠ADB=∠BDC=40°,∴∠AOB=2∠ADB=80°.又∵M是OD上一点,∴∠ADB≤∠AMB≤∠AOB,即40°≤∠AMB≤80°,则不符合条件的只有85°.
二、填空题
9.
【答案】3
10.
【答案】50 [解析]
由三角形的内角和定理,得∠B+∠C=180°-∠A.再由OB=OD=OC=OE,得到∠BDO=∠B,∠CEO=∠C.在等腰三角形BOD和等腰三角形COE中,∠DOB+∠EOC=180°-2∠B+180°-2∠C=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以∠DOE=180°-2∠A=50°.
11.
【答案】8 [解析]
由题意可得A,P,B,C在同一个圆上,所以当BP为圆的直径时,BP最大,此时∠PAB=90°.过点C作CD⊥AB于点D,可求得AB=4
,进而可求得BP的最大值为8.
12.
【答案】5 [解析]
∵OE过圆心且与PA垂直,
∴PE=EA.
同理PF=FB,∴EF是△PAB的中位线,
∴EF=AB=5.
13.
【答案】6 90 [解析]
∵AB为⊙M的直径,
∴AB=4.
当点O到AB的距离最大时,△AOB的面积最大,此时AB⊥x轴于点M,
∴△AOB的面积的最大值为×4×3=6,∠AMO=90°.
即此时A,B两点所在直线与x轴的夹角等于90°.
14.
【答案】215 [解析]
连接CE,则∠B+∠AEC=180°,∠DEC=∠CAD=35°,∴∠B+∠AED=(∠B+∠AEC)+∠DEC=180°+35°=215°.
15.
【答案】(-4,-7) [解析]
过点P作PH⊥MN于点H,连接PM,则MH=MN=3,OH=OM+MH=7.由勾股定理,得PH=4,∴圆心P的坐标为(-4,-7).
16.
【答案】4 [解析]
如图,当CD∥AB时,PM的长最大,连接OM,OC.
∵CD∥AB,CP⊥AB,
∴CP⊥CD.
∵M为CD的中点,OM过点O,
∴OM⊥CD,
∴∠OMC=∠PCD=∠CPO=90°,
∴四边形CPOM是矩形,
∴PM=OC.
∵⊙O的直径AB=8,
∴半径OC=4,∴PM=4.
三、解答题
17.
【答案】
证明:∵AB,CD是⊙O的两条直径,
∴∠AOC=∠BOD,∴AC=BD.
又∵BE=BD,
∴AC=BE,∴=.
18.
【答案】
证明:连接OM,ON,OA,OC,如图所示.
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,AM=AB,CN=CD.
又∵AB=CD,∴AM=CN.
在Rt△AOM和Rt△CON中,
∴Rt△AOM≌Rt△CON(HL),
∴OM=ON,∴∠OMN=∠ONM,
∴∠AMO+∠OMN=∠CNO+∠ONM,
即∠AMN=∠CNM.
19.
【答案】
解:(1)设⊙E切BC于点M,连接EM,则EM⊥BC.又线段AE的延长线交BC于点F,∠AFC≠90°,∴EF>EM,∴点F在△ABC的内切圆⊙E外.
(2)证明:∵点E是△ABC的内心,
∴∠BAD=∠CAD,∠ABE=∠CBE.
∵∠CBD=∠CAD,∴∠BAD=∠CBD.
∵∠BED=∠ABE+∠BAD,∠EBD=∠CBE+
∠CBD,
∴∠BED=∠EBD,∴ED=BD.
(3)如图①,连接CD.
设△ABC的外接圆为⊙O.
∵∠BAC=90°,∴BC是⊙O的直径,
∴∠BDC=90°.
∵⊙O的直径是6,∴BC=6.
∵E为△ABC的内切圆的圆心,
∴∠BAD=∠CAD,∴BD=CD.
又∵BD2+CD2=BC2,∴BD=CD=3
.
(4)B,C,E三点可以确定一个圆.
如图②,连接CD.
∵点E是△ABC的内心,
∴∠BAD=∠CAD,
∴BD=CD.
又由(2)可知ED=BD,
∴BD=CD=ED,
∴B,C,E三点确定的圆的圆心为点D,半径为BD(或ED,CD)的长度.
20.
【答案】
解:(1)60
(2)①如图(a).
∵四边形OBCD为平行四边形,
∴∠BOD=∠BCD,∠OBC=∠ODC.
又∵∠BAD+∠BCD=180°,∠BAD=∠BOD,
∴∠BOD+∠BOD=180°,解得∠BOD=120°,∴∠BAD=∠BOD=×120°=60°,∠OBC=∠ODC=180°-∠BOD=180°-120°=60°.
又∵∠ABC+∠ADC=180°,
∴∠OBA+∠ODA=∠ABC+∠ADC-(∠OBC+∠ODC)=180°-(60°+60°)=60°.
②如图(b)所示,连接AO.
∵OA=OB,
∴∠OBA=∠OAB.
∵OA=OD,
∴∠OAD=∠ODA.
∵∠OAB=∠OAD+∠BAD,
∴∠OBA=∠ODA+∠BAD=∠ODA+60°.
如图(c),同理可得∠ODA=∠OBA+60°.
初三数学
24.1
圆的有关性质
同步课时训练
一、选择题
1.
已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
A.45°
B.35°
C.25°
D.20°
2.
小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是
( )
A.AB,AC边上的中线的交点
B.AB,AC边上的垂直平分线的交点
C.AB,AC边上的高所在直线的交点
D.∠BAC与∠ABC的角平分线的交点
3.
如图,在直角坐标系中,以原点为圆心,半径为5的圆内有一点P(0,-3),那么经过点P的所有弦中,最短的弦的长为( )
A.4
B.5
C.8
D.10
4.
如图,著名水乡乌镇的一圆拱桥的拱顶到水面的距离CD为8
m,水面宽AB为8
m,则拱桥的半径OC为( )
A.4
m
B.5
m
C.6
m
D.8
m
5.
如图,AD是⊙O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB相交于点P,下列结论错误的是( )
A.AP=2OP
B.CD=2OP
C.OB⊥AC
D.AC平分OB
6.
2019·聊城
如图,BC是半圆O的直径,D,E是上的两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为( )
A.35°
B.38°
C.40°
D.42°
7.
如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
8.
如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
A.45°
B.60°
C.75°
D.85°
二、填空题
9.
如图,AB为⊙O的直径,CD⊥AB.若AB=10,CD=8,则圆心O到弦CD的距离为________.
10.
如图,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE.若∠A=65°,则∠DOE=________°.
11.
如图,已知等腰三角形ABC中,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,则BP的最大值为________.
12.
如图0,A,B是⊙O上的两点,AB=10,P是⊙O上的动点(点P与A,B两点不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=________.
13.
如图,平面直角坐标系xOy中,点M的坐标为(3,0),⊙M的半径为2,过点M的直线与⊙M的交点分别为A,B,则△AOB的面积的最大值为________,此时A,B两点所在直线与x轴的夹角等于________°.
14.
如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=________°.
15.
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),则圆心P的坐标为________.
16.
如图,定长弦CD在以AB为直径的⊙O上滑动(点C,D与点A,B不重合),M是CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=8,PM=l,则l的最大值是________.
三、解答题
17.
如图所示,AB,CD是⊙O的两条直径,弦BE=BD.求证:=.
18.
已知:如图5,在⊙O中,M,N分别为弦AB,CD的中点,AB=CD,AB不平行于CD.
求证:∠AMN=∠CNM.
19.
如图,点E是△ABC的内心,线段AE的延长线交BC于点F(∠AFC≠90°),交△ABC的外接圆于点D.
(1)求点F与△ABC的内切圆⊙E的位置关系;
(2)求证:ED=BD;
(3)若∠BAC=90°,△ABC的外接圆的直径是6,求BD的长;
(4)B,C,E三点可以确定一个圆吗?若可以,则它们确定的圆的圆心和半径分别是什么?若不可以,请说明理由.
20.
如图,四边形OBCD中的三个顶点在⊙O上,A是优弧BAD上的一个动点(不与点B,D重合).
(1)当圆心O在∠BAD的内部时,若∠BOD=120°,则∠OBA+∠ODA=________°.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.
人教版
初三数学
24.1
圆的有关性质
同步课时训练-答案
一、选择题
1.
【答案】A
2.
【答案】B [解析]本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点,故选B.
3.
【答案】C [解析]
过点P作弦AB⊥OP,连接OB,如图.
则PB=AP,∴AB=2BP=2
.
再过点P任作一条弦MN,过点O作OG⊥MN于点G,连接ON.
则MN=2GN=2
.
∵OP>OG,OB=ON,∴MN>AB,
∴AB是⊙O中的过点P最短的弦.
在Rt△OPB中,PO=3,OB=5,由勾股定理,得PB=4,则AB=2PB=8.
4.
【答案】B [解析]
如图,连接BO.
由题意可得AD=BD=4
m.
设⊙O的半径OC=x
m,则DO=(8-x)m.
由勾股定理可得x2=(8-x)2+42,解得x=5.
故拱桥的半径OC为5
m.
5.
【答案】A [解析]
∵AD是⊙O的直径,
∴∠ACD=90°.
∵四边形OBCD是平行四边形,
∴CD∥OB,CD=OB,∴∠CPO=90°,
即OB⊥AC,∴选项C正确;
∴CP=AP.又∵OA=OD,
∴OP是△ACD的中位线,
∴CD=2OP,∴选项B正确;
∴CD=OB=2OP,即P是OB的中点,
∴AC平分OB,∴选项D正确.
6.
【答案】C
7.
【答案】C
8.
【答案】D [解析]
连接AD,OA,OB.∵B是的中点,∴∠ADB=∠BDC=40°,∴∠AOB=2∠ADB=80°.又∵M是OD上一点,∴∠ADB≤∠AMB≤∠AOB,即40°≤∠AMB≤80°,则不符合条件的只有85°.
二、填空题
9.
【答案】3
10.
【答案】50 [解析]
由三角形的内角和定理,得∠B+∠C=180°-∠A.再由OB=OD=OC=OE,得到∠BDO=∠B,∠CEO=∠C.在等腰三角形BOD和等腰三角形COE中,∠DOB+∠EOC=180°-2∠B+180°-2∠C=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以∠DOE=180°-2∠A=50°.
11.
【答案】8 [解析]
由题意可得A,P,B,C在同一个圆上,所以当BP为圆的直径时,BP最大,此时∠PAB=90°.过点C作CD⊥AB于点D,可求得AB=4
,进而可求得BP的最大值为8.
12.
【答案】5 [解析]
∵OE过圆心且与PA垂直,
∴PE=EA.
同理PF=FB,∴EF是△PAB的中位线,
∴EF=AB=5.
13.
【答案】6 90 [解析]
∵AB为⊙M的直径,
∴AB=4.
当点O到AB的距离最大时,△AOB的面积最大,此时AB⊥x轴于点M,
∴△AOB的面积的最大值为×4×3=6,∠AMO=90°.
即此时A,B两点所在直线与x轴的夹角等于90°.
14.
【答案】215 [解析]
连接CE,则∠B+∠AEC=180°,∠DEC=∠CAD=35°,∴∠B+∠AED=(∠B+∠AEC)+∠DEC=180°+35°=215°.
15.
【答案】(-4,-7) [解析]
过点P作PH⊥MN于点H,连接PM,则MH=MN=3,OH=OM+MH=7.由勾股定理,得PH=4,∴圆心P的坐标为(-4,-7).
16.
【答案】4 [解析]
如图,当CD∥AB时,PM的长最大,连接OM,OC.
∵CD∥AB,CP⊥AB,
∴CP⊥CD.
∵M为CD的中点,OM过点O,
∴OM⊥CD,
∴∠OMC=∠PCD=∠CPO=90°,
∴四边形CPOM是矩形,
∴PM=OC.
∵⊙O的直径AB=8,
∴半径OC=4,∴PM=4.
三、解答题
17.
【答案】
证明:∵AB,CD是⊙O的两条直径,
∴∠AOC=∠BOD,∴AC=BD.
又∵BE=BD,
∴AC=BE,∴=.
18.
【答案】
证明:连接OM,ON,OA,OC,如图所示.
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,AM=AB,CN=CD.
又∵AB=CD,∴AM=CN.
在Rt△AOM和Rt△CON中,
∴Rt△AOM≌Rt△CON(HL),
∴OM=ON,∴∠OMN=∠ONM,
∴∠AMO+∠OMN=∠CNO+∠ONM,
即∠AMN=∠CNM.
19.
【答案】
解:(1)设⊙E切BC于点M,连接EM,则EM⊥BC.又线段AE的延长线交BC于点F,∠AFC≠90°,∴EF>EM,∴点F在△ABC的内切圆⊙E外.
(2)证明:∵点E是△ABC的内心,
∴∠BAD=∠CAD,∠ABE=∠CBE.
∵∠CBD=∠CAD,∴∠BAD=∠CBD.
∵∠BED=∠ABE+∠BAD,∠EBD=∠CBE+
∠CBD,
∴∠BED=∠EBD,∴ED=BD.
(3)如图①,连接CD.
设△ABC的外接圆为⊙O.
∵∠BAC=90°,∴BC是⊙O的直径,
∴∠BDC=90°.
∵⊙O的直径是6,∴BC=6.
∵E为△ABC的内切圆的圆心,
∴∠BAD=∠CAD,∴BD=CD.
又∵BD2+CD2=BC2,∴BD=CD=3
.
(4)B,C,E三点可以确定一个圆.
如图②,连接CD.
∵点E是△ABC的内心,
∴∠BAD=∠CAD,
∴BD=CD.
又由(2)可知ED=BD,
∴BD=CD=ED,
∴B,C,E三点确定的圆的圆心为点D,半径为BD(或ED,CD)的长度.
20.
【答案】
解:(1)60
(2)①如图(a).
∵四边形OBCD为平行四边形,
∴∠BOD=∠BCD,∠OBC=∠ODC.
又∵∠BAD+∠BCD=180°,∠BAD=∠BOD,
∴∠BOD+∠BOD=180°,解得∠BOD=120°,∴∠BAD=∠BOD=×120°=60°,∠OBC=∠ODC=180°-∠BOD=180°-120°=60°.
又∵∠ABC+∠ADC=180°,
∴∠OBA+∠ODA=∠ABC+∠ADC-(∠OBC+∠ODC)=180°-(60°+60°)=60°.
②如图(b)所示,连接AO.
∵OA=OB,
∴∠OBA=∠OAB.
∵OA=OD,
∴∠OAD=∠ODA.
∵∠OAB=∠OAD+∠BAD,
∴∠OBA=∠ODA+∠BAD=∠ODA+60°.
如图(c),同理可得∠ODA=∠OBA+60°.
同课章节目录
