人教版 初三数学 24.2 点和圆、直线和圆的位置关系 同步课时训练(word含答案)
文档属性
| 名称 | 人教版 初三数学 24.2 点和圆、直线和圆的位置关系 同步课时训练(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 657.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 15:47:06 | ||
图片预览



文档简介
人教版
初三数学
24.2
点和圆、直线和圆的位置关系
同步课时训练
一、选择题
1.
如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB等于( )
A.2
B.3
C.4
D.5
2.
2019·益阳如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A.PA=PB
B.∠BPD=∠APD
C.AB⊥PD
D.AB平分PD
3.
已知⊙O的半径为2,点P到圆心O的距离为4,则点P在( )
A.⊙O内
B.⊙O上
C.⊙O外
D.无法确定
4.
如图,在矩形ABCD中,AB=3,AD=4.若以点A为圆心,4为半径作⊙A,则下列各点中在⊙A外的是( )
A.点A
B.点B
C.点C
D.点D
5.
如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC的延长线于点P,则PA的长为( )
A.2
B.
C.
D.
6.
《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题:“今有勾八步,股十五步,问勾中容圆径几何.”其意思是:“今有直角三角形(如图),勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)的直径是多少.”答案是
( )
A.3步
B.5步
C.6步
D.8步
7.
如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在⊙O外、⊙O内、⊙O上,则原点O的位置应该在( )
图
A.点A与点B之间靠近点A
B.点A与点B之间靠近点B
C.点B与点C之间靠近点B
D.点B与点C之间靠近点C
8.
如图0,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
图0
A.
B.2
C.
D.
二、填空题
9.
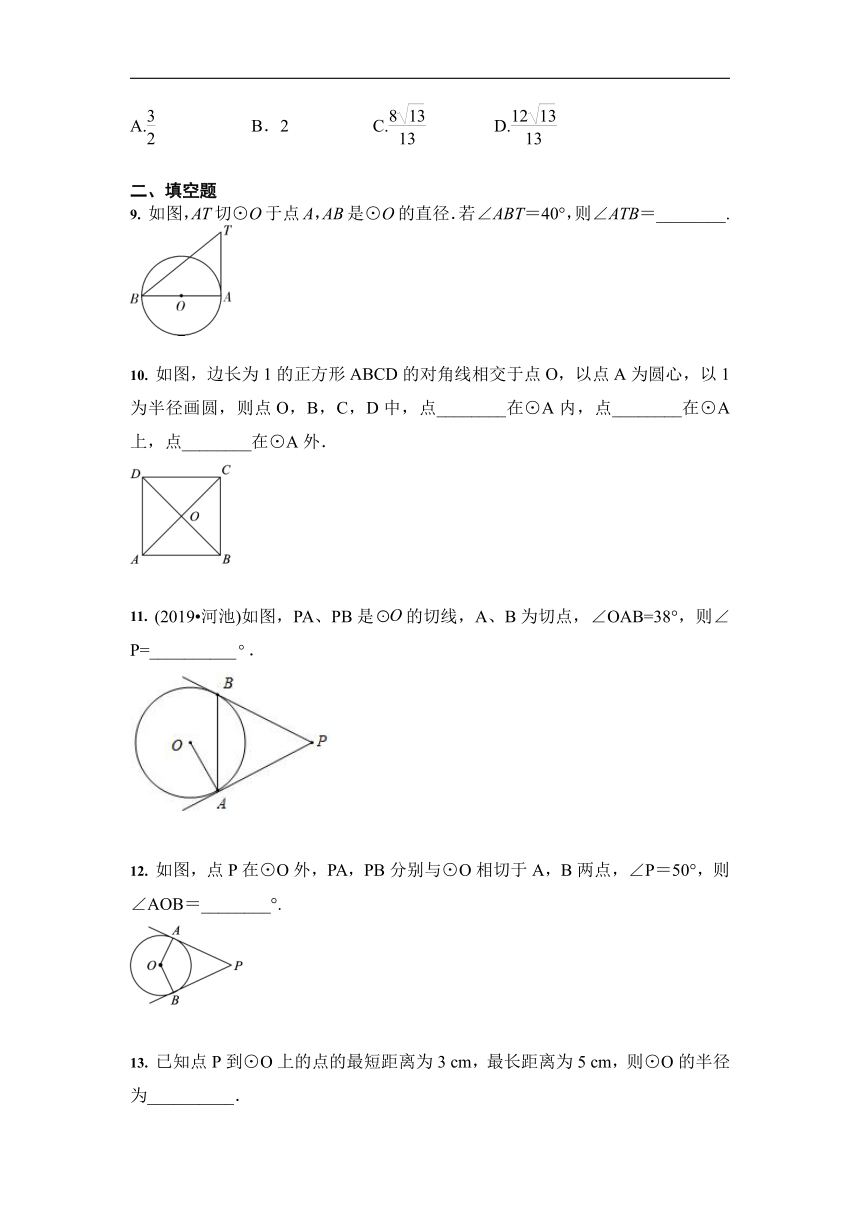
如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=________.
10.
如图,边长为1的正方形ABCD的对角线相交于点O,以点A为圆心,以1为半径画圆,则点O,B,C,D中,点________在⊙A内,点________在⊙A上,点________在⊙A外.
11.
(2019?河池)如图,PA、PB是的切线,A、B为切点,∠OAB=38°,则∠P=__________.
12.
如图,点P在⊙O外,PA,PB分别与⊙O相切于A,B两点,∠P=50°,则∠AOB=________°.
13.
已知点P到⊙O上的点的最短距离为3
cm,最长距离为5
cm,则⊙O的半径为__________.
14.
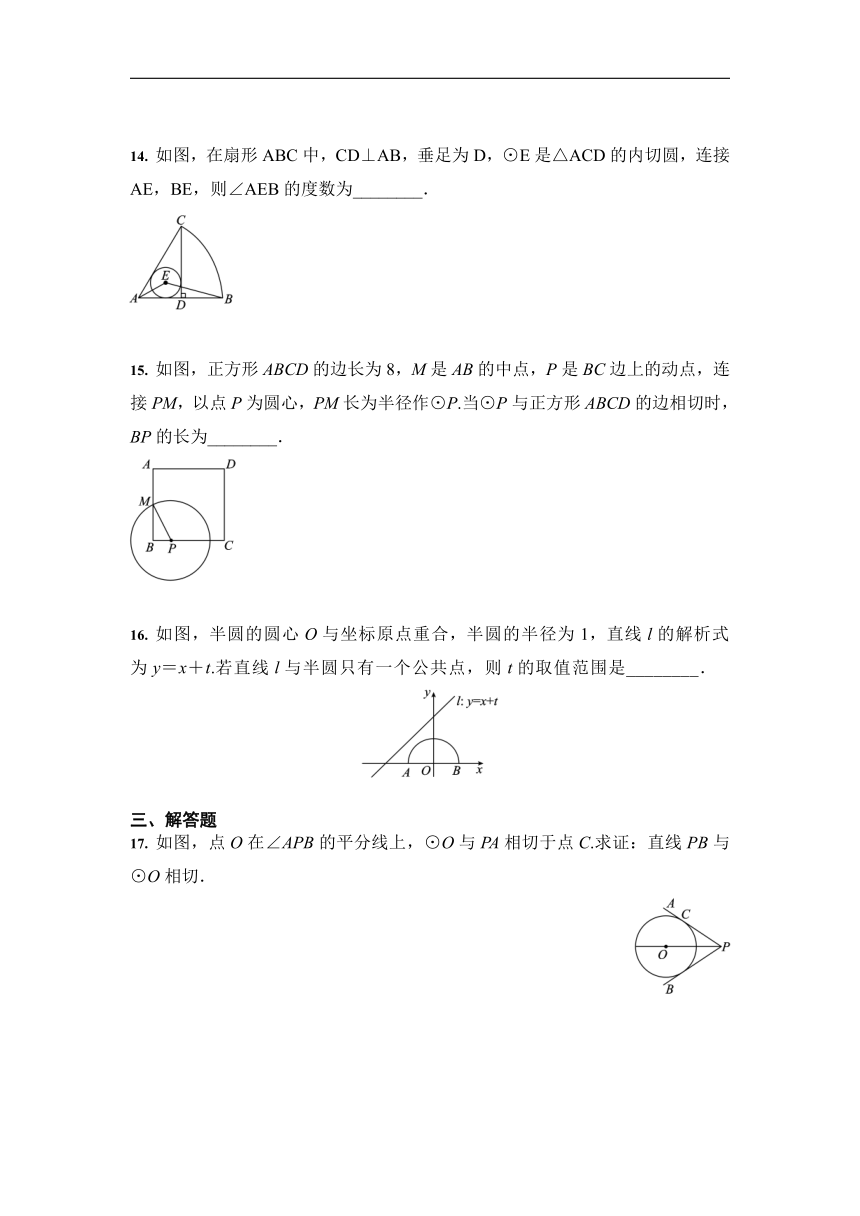
如图,在扇形ABC中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为________.
15.
如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________.
16.
如图,半圆的圆心O与坐标原点重合,半圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个公共点,则t的取值范围是________.
三、解答题
17.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.求证:直线PB与⊙O相切.
18.
已知AB=4
cm,画图并用文字说明满足下列条件的图形.
(1)到点A和点B的距离都等于3
cm的所有点组成的图形;
(2)到点A和点B的距离都不大于3
cm的所有点组成的图形;
(3)到点A的距离大于3
cm,且到点B的距离小于3
cm的所有点组成的图形.
19.
如图,⊙O与△ABC的AC边相切于点C,与AB,BC边分别交于点D,E,DE∥OA,CE是⊙O的直径.
求证:AB是⊙O的切线.
20.
已知:如图,以点O为圆心的两个同心圆中,大圆的弦AB=CD,且AB是小圆的切线,切点为M.求证:CD是小圆的切线.
人教版
初三数学
24.2
点和圆、直线和圆的位置关系
同步课时训练-答案
一、选择题
1.
【答案】B
2.
【答案】D
3.
【答案】C
4.
【答案】C
5.
【答案】B [解析]
连接OA.因为∠ABC=30°,所以∠AOC=60°.因为PA为⊙O的切线,所以∠OAP=90°,所以∠P=90°-∠AOC=30°.因为OA=OC=1,所以OP=2OA=1,
所以PA=.
6.
【答案】C
7.
【答案】C [解析]
如图.
8.
【答案】B [解析]
∵∠ABC=90°,
∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,
∴∠ABP+∠PAB=90°,∴∠APB=90°,
∴点P在以AB为直径的圆上,设圆心为O,连接OC交⊙O于点P,此时CP最小.
在Rt△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC=5,OP=OB=3,∴PC=OC-OP=5-3=2,∴PC的最小值为2.
二、填空题
9.
【答案】50° 【解析】∵AT是⊙O的切线,AB是⊙O的直径,∴∠BAT=90°,在Rt△BAT中,∵∠ABT=40°,∴∠ATB=50°.
10.
【答案】O B,D C [解析]
∵四边形ABCD为正方形,∴AC⊥BD,AO=BO=CO=DO.
设AO=BO=x.
由勾股定理,得AO2+BO2=AB2,即x2+x2=12,解得x=(负值已舍去),
∴AO=<1,AC=>1,∴点O在⊙A内,点B,D在⊙A上,点C在⊙A外.
11.
【答案】76
【解析】∵是的切线,∴,
∴,∴,
∴,故答案为:76.
12.
【答案】130
13.
【答案】1
cm或4
cm [解析]
若点P在⊙O内,如图①.∵AP=3
cm,BP=5
cm,
∴AB=8
cm,∴OA=4
cm;
若点P在⊙O外,如图②.
∵AP=3
cm,BP=5
cm,
∴AB=2
cm,
∴OA=1
cm.
14.
【答案】135° [解析]
连接CE.∵∠ADC=90°,∴∠DAC+∠DCA=90°.∵⊙E内切于△ADC,∴∠EAC+∠ECA=45°,∴∠AEC=135°.由“边角边”可知△AEC≌△AEB,∴∠AEB=∠AEC=135°.
15.
【答案】3或4
[解析]
如图①,当⊙P与CD边相切时,设PC=PM=x.
在Rt△PBM中,
∵PM2=BM2+BP2,
∴x2=42+(8-x)2,
∴x=5,∴PC=5,
∴BP=BC-PC=8-5=3.
如图②,当⊙P与AD边相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形,
∴PM=PK=CD=2BM,
∴BM=4,PM=8,
在Rt△PBM中,BP==4
.
综上所述,BP的长为3或4
.
16.
【答案】t=或-1≤t<1 [解析]
若直线与半圆只有一个公共点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).
直线y=x+t与x轴所形成的锐角是45°.
当点O到直线l的距离OC=1时,直线l与半圆O相切,设直线l与y轴交于点D,则OD=,即t=.
当直线过点A时,把A(-1,0)代入直线l的解析式,得t=y-x=1.
当直线过点B时,把B(1,0)代入直线l的解析式,得t=y-x=-1.
即当t=或-1≤t<1时,直线和半圆只有一个公共点.
故答案为t=或-1≤t<1.
三、解答题
17.
【答案】
证明:如图,连接OC,过点O作OD⊥PB于点D.
∵⊙O与PA相切于点C,
∴OC⊥PA.
∵点O在∠APB的平分线上,OC⊥PA,OD⊥PB,
∴OD=OC,∴直线PB与⊙O相切.
18.
【答案】
解:(1)如图①中的点C和点D.
(2)如图①中的阴影部分(包括边界).
(3)如图②中的阴影部分(不包括边界).
19.
【答案】
证明:如图,连接OD.
∵DE∥OA,
∴∠AOC=∠OED,∠AOD=∠ODE.
∵OD=OE,
∴∠OED=∠ODE,
∴∠AOC=∠AOD.
又∵OA=OA,OC=OD,
∴△AOC≌△AOD(SAS),
∴∠ADO=∠ACO.
∵CE是⊙O的直径,AC为⊙O的切线,
∴OC⊥AC,∴∠ACO=90°,
∴∠ADO=90°,即OD⊥AB.
又∵OD为⊙O的半径,∴AB是⊙O的切线.
20.
【答案】
证明:如图,连接OM,OA,OC,过点O作ON⊥CD于点N.
∵AB与小圆相切,切点为M,
∴OM⊥AB,∴M,N分别为AB,CD的中点,
∴AM=BM=AB,CN=DN=CD.
又∵AB=CD,∴AM=CN.
在Rt△AOM和Rt△CON中,
∴Rt△AOM≌Rt△CON(HL),
∴OM=ON,即ON是⊙O的半径,
∴CD是小圆的切线.
初三数学
24.2
点和圆、直线和圆的位置关系
同步课时训练
一、选择题
1.
如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB等于( )
A.2
B.3
C.4
D.5
2.
2019·益阳如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A.PA=PB
B.∠BPD=∠APD
C.AB⊥PD
D.AB平分PD
3.
已知⊙O的半径为2,点P到圆心O的距离为4,则点P在( )
A.⊙O内
B.⊙O上
C.⊙O外
D.无法确定
4.
如图,在矩形ABCD中,AB=3,AD=4.若以点A为圆心,4为半径作⊙A,则下列各点中在⊙A外的是( )
A.点A
B.点B
C.点C
D.点D
5.
如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC的延长线于点P,则PA的长为( )
A.2
B.
C.
D.
6.
《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题:“今有勾八步,股十五步,问勾中容圆径几何.”其意思是:“今有直角三角形(如图),勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)的直径是多少.”答案是
( )
A.3步
B.5步
C.6步
D.8步
7.
如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在⊙O外、⊙O内、⊙O上,则原点O的位置应该在( )
图
A.点A与点B之间靠近点A
B.点A与点B之间靠近点B
C.点B与点C之间靠近点B
D.点B与点C之间靠近点C
8.
如图0,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
图0
A.
B.2
C.
D.
二、填空题
9.
如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=________.
10.
如图,边长为1的正方形ABCD的对角线相交于点O,以点A为圆心,以1为半径画圆,则点O,B,C,D中,点________在⊙A内,点________在⊙A上,点________在⊙A外.
11.
(2019?河池)如图,PA、PB是的切线,A、B为切点,∠OAB=38°,则∠P=__________.
12.
如图,点P在⊙O外,PA,PB分别与⊙O相切于A,B两点,∠P=50°,则∠AOB=________°.
13.
已知点P到⊙O上的点的最短距离为3
cm,最长距离为5
cm,则⊙O的半径为__________.
14.
如图,在扇形ABC中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为________.
15.
如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________.
16.
如图,半圆的圆心O与坐标原点重合,半圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个公共点,则t的取值范围是________.
三、解答题
17.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.求证:直线PB与⊙O相切.
18.
已知AB=4
cm,画图并用文字说明满足下列条件的图形.
(1)到点A和点B的距离都等于3
cm的所有点组成的图形;
(2)到点A和点B的距离都不大于3
cm的所有点组成的图形;
(3)到点A的距离大于3
cm,且到点B的距离小于3
cm的所有点组成的图形.
19.
如图,⊙O与△ABC的AC边相切于点C,与AB,BC边分别交于点D,E,DE∥OA,CE是⊙O的直径.
求证:AB是⊙O的切线.
20.
已知:如图,以点O为圆心的两个同心圆中,大圆的弦AB=CD,且AB是小圆的切线,切点为M.求证:CD是小圆的切线.
人教版
初三数学
24.2
点和圆、直线和圆的位置关系
同步课时训练-答案
一、选择题
1.
【答案】B
2.
【答案】D
3.
【答案】C
4.
【答案】C
5.
【答案】B [解析]
连接OA.因为∠ABC=30°,所以∠AOC=60°.因为PA为⊙O的切线,所以∠OAP=90°,所以∠P=90°-∠AOC=30°.因为OA=OC=1,所以OP=2OA=1,
所以PA=.
6.
【答案】C
7.
【答案】C [解析]
如图.
8.
【答案】B [解析]
∵∠ABC=90°,
∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,
∴∠ABP+∠PAB=90°,∴∠APB=90°,
∴点P在以AB为直径的圆上,设圆心为O,连接OC交⊙O于点P,此时CP最小.
在Rt△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC=5,OP=OB=3,∴PC=OC-OP=5-3=2,∴PC的最小值为2.
二、填空题
9.
【答案】50° 【解析】∵AT是⊙O的切线,AB是⊙O的直径,∴∠BAT=90°,在Rt△BAT中,∵∠ABT=40°,∴∠ATB=50°.
10.
【答案】O B,D C [解析]
∵四边形ABCD为正方形,∴AC⊥BD,AO=BO=CO=DO.
设AO=BO=x.
由勾股定理,得AO2+BO2=AB2,即x2+x2=12,解得x=(负值已舍去),
∴AO=<1,AC=>1,∴点O在⊙A内,点B,D在⊙A上,点C在⊙A外.
11.
【答案】76
【解析】∵是的切线,∴,
∴,∴,
∴,故答案为:76.
12.
【答案】130
13.
【答案】1
cm或4
cm [解析]
若点P在⊙O内,如图①.∵AP=3
cm,BP=5
cm,
∴AB=8
cm,∴OA=4
cm;
若点P在⊙O外,如图②.
∵AP=3
cm,BP=5
cm,
∴AB=2
cm,
∴OA=1
cm.
14.
【答案】135° [解析]
连接CE.∵∠ADC=90°,∴∠DAC+∠DCA=90°.∵⊙E内切于△ADC,∴∠EAC+∠ECA=45°,∴∠AEC=135°.由“边角边”可知△AEC≌△AEB,∴∠AEB=∠AEC=135°.
15.
【答案】3或4
[解析]
如图①,当⊙P与CD边相切时,设PC=PM=x.
在Rt△PBM中,
∵PM2=BM2+BP2,
∴x2=42+(8-x)2,
∴x=5,∴PC=5,
∴BP=BC-PC=8-5=3.
如图②,当⊙P与AD边相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形,
∴PM=PK=CD=2BM,
∴BM=4,PM=8,
在Rt△PBM中,BP==4
.
综上所述,BP的长为3或4
.
16.
【答案】t=或-1≤t<1 [解析]
若直线与半圆只有一个公共点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).
直线y=x+t与x轴所形成的锐角是45°.
当点O到直线l的距离OC=1时,直线l与半圆O相切,设直线l与y轴交于点D,则OD=,即t=.
当直线过点A时,把A(-1,0)代入直线l的解析式,得t=y-x=1.
当直线过点B时,把B(1,0)代入直线l的解析式,得t=y-x=-1.
即当t=或-1≤t<1时,直线和半圆只有一个公共点.
故答案为t=或-1≤t<1.
三、解答题
17.
【答案】
证明:如图,连接OC,过点O作OD⊥PB于点D.
∵⊙O与PA相切于点C,
∴OC⊥PA.
∵点O在∠APB的平分线上,OC⊥PA,OD⊥PB,
∴OD=OC,∴直线PB与⊙O相切.
18.
【答案】
解:(1)如图①中的点C和点D.
(2)如图①中的阴影部分(包括边界).
(3)如图②中的阴影部分(不包括边界).
19.
【答案】
证明:如图,连接OD.
∵DE∥OA,
∴∠AOC=∠OED,∠AOD=∠ODE.
∵OD=OE,
∴∠OED=∠ODE,
∴∠AOC=∠AOD.
又∵OA=OA,OC=OD,
∴△AOC≌△AOD(SAS),
∴∠ADO=∠ACO.
∵CE是⊙O的直径,AC为⊙O的切线,
∴OC⊥AC,∴∠ACO=90°,
∴∠ADO=90°,即OD⊥AB.
又∵OD为⊙O的半径,∴AB是⊙O的切线.
20.
【答案】
证明:如图,连接OM,OA,OC,过点O作ON⊥CD于点N.
∵AB与小圆相切,切点为M,
∴OM⊥AB,∴M,N分别为AB,CD的中点,
∴AM=BM=AB,CN=DN=CD.
又∵AB=CD,∴AM=CN.
在Rt△AOM和Rt△CON中,
∴Rt△AOM≌Rt△CON(HL),
∴OM=ON,即ON是⊙O的半径,
∴CD是小圆的切线.
同课章节目录
