苏科版九年级数学下册5.5用二次函数解决问题复习-巩固训练(word解析版)
文档属性
| 名称 | 苏科版九年级数学下册5.5用二次函数解决问题复习-巩固训练(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 00:00:00 | ||
图片预览




文档简介
5.5用二次函数解决问题
复习
-苏科版九年级数学下册
巩固训练
一、选择题
1、如图,利用一面墙,其他三边用80米长的篱笆围成一块矩形场地,墙长为30米,则围成矩形场地的最大面积为( )
A.800平方米
B.750平方米
C.600平方米
D.2400平方米
2、小敏用一根长为8
cm的细铁丝围成矩形,则矩形的最大面积是( )
A.4
cm2
B.8
cm2
C.16
cm2
D.32
cm2
3、小敏在某次投篮中,球的运动线路是抛物线y=-x2+3.5的一部分(如图5-5-5).若命中篮圈中心,则他与篮底的距离l是( )
A.3.5
m
B.4
m
C.4.5
m
D.4.6
m
4、如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m
B.4m
C.4
m
D.4m
5、广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠和喷头的水平距离x(米)的函数解析式是y=x2+6x(0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是( )
A.1米
B.2米
C.5米
D.6米
6、某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价为偶数提高(
)
A.
8元或10元
B.
12元
C.
8元
D.
10元
7、用长为12
m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,垂足分别为A,B,∠C=∠D=∠E.设CD=DE=x
m,五边形ABCDE的面积为S
m2,则S的最大值为( )
A.12
B.12
C.24
D.没有最大值
8、如图,将一个小球从斜坡上的点O处抛出,小球的抛出路线可以用二次函数y=4x-x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5
m时,小球距点O的水平距离为3
m
B.小球距点O的水平距离超过4
m后呈下降趋势
C.小球落地点距点O的水平距离为7
m
D.小球距点O的水平距离为2.5
m和5.5
m时的高度相同
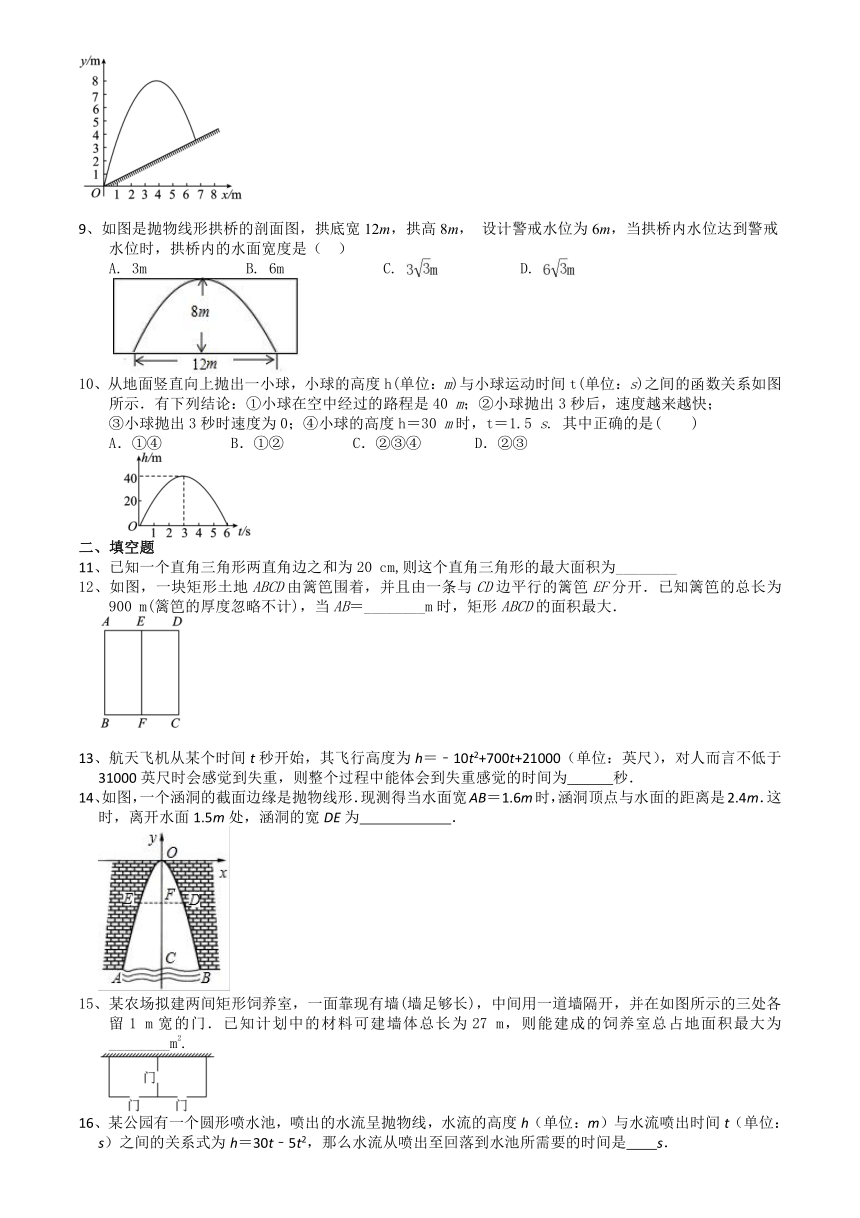
9、如图是抛物线形拱桥的剖面图,拱底宽12m,拱高8m,
设计警戒水位为6m,当拱桥内水位达到警戒水位时,拱桥内的水面宽度是(
)
A.
3m
B.
6m
C.
D.
10、从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.有下列结论:①小球在空中经过的路程是40
m;②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;④小球的高度h=30
m时,t=1.5
s.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②③
二、填空题
11、已知一个直角三角形两直角边之和为20
cm,则这个直角三角形的最大面积为________
12、如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900
m(篱笆的厚度忽略不计),当AB=________m时,矩形ABCD的面积最大.
13、航天飞机从某个时间t秒开始,其飞行高度为h=﹣10t2+700t+21000(单位:英尺),对人而言不低于31000英尺时会感觉到失重,则整个过程中能体会到失重感觉的时间为 秒.
14、如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽AB=1.6m时,涵洞顶点与水面的距离是2.4m.这时,离开水面1.5m处,涵洞的宽DE为 .
15、某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1
m宽的门.已知计划中的材料可建墙体总长为27
m,则能建成的饲养室总占地面积最大为________m2.
16、某公园有一个圆形喷水池,喷出的水流呈抛物线,水流的高度h(单位:m)与水流喷出时间t(单位:s)之间的关系式为h=30t﹣5t2,那么水流从喷出至回落到水池所需要的时间是 s.
17、如图是某地一座抛物线形拱桥,桥拱在竖直平面内与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9
m,AB=36
m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7
m,则DE的长为________m.
18、铅球行进高度y(m)与水平距离x(m)之间的关系为y=﹣x2+x+,铅球推出后最大高度是 m,铅球落地时的水平距离是 m.
三、解答题
19、如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-x+3x+1的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
20、如图,已知A,B,C,D为矩形的四个顶点,AB=16
cm,AD=6
cm,动点P,Q分别从点A,C同时出发,点P以3
cm/s的速度向点B移动,点Q以2
cm/s的速度向点D移动,当其中一点到达终点时,另一点也随之停止移动.
(1)经过几秒,P,Q两点之间的距离是10
cm?
(2)P,Q两点之间的距离何时最小?
21、一自动喷灌设备的喷流情况如图所示,设水管AB在高出地面1.5米的B处有一自动旋转的喷水头,一瞬间喷出的水流是抛物线状,喷头B与水流最高点C的连线成45°角,水流最高点C比喷头高2米,
求:(1)点C的坐标;(2)此抛物线的解析式;(3)水流落点D到点A的距离.
22、如图所示,隧道的截面由抛物线和长方形构成,长方形的长是12
m,宽是4
m.按照图中所示的直角坐标系,抛物线可以用
y=x+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3
m时,到地面OA的距离为m.
(1)求该抛物线的函数解析式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6
m,宽为4
m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8
m,那么两排灯的水平距离最小是多少?
5.5用二次函数解决问题
复习
-苏科版九年级数学下册
巩固训练(答案)
一、选择题
1、如图,利用一面墙,其他三边用80米长的篱笆围成一块矩形场地,墙长为30米,则围成矩形场地的最大面积为( )
A.800平方米
B.750平方米
C.600平方米
D.2400平方米
[解析]
设矩形场地中平行于墙的边长为x米,则垂直于墙的边长为米,
围成矩形场地的面积为y平方米,
则y=x·=-x2+40x=-(x-40)2+800.
∵a<0,∴x<40时,y随x的增大而增大,由于墙长为30米,∴0∴当x=30时,y取得最大值,为-×(30-40)2+800=750.
故选B
2、小敏用一根长为8
cm的细铁丝围成矩形,则矩形的最大面积是( A )
A.4
cm2
B.8
cm2
C.16
cm2
D.32
cm2
[解析]
设矩形的一边长为x
cm,则另一边长为cm,
故矩形的面积S=x=-x2+4x=-(x-2)2+4,所
以当x=2时,S最大值=4.故矩形的最大面积为4
cm2.
3、小敏在某次投篮中,球的运动线路是抛物线y=-x2+3.5的一部分(如图5-5-5).若命中篮圈中心,则他与篮底的距离l是( )
A.3.5
m
B.4
m
C.4.5
m
D.4.6
m
[解析]
当y=3.05时,-x2+3.5=3.05,解得x1=-1.5(舍去),x2=1.5,
∴l=2.5+1.5=4(m).
故选B.
4、如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m
B.4m
C.4
m
D.4m
【解答】解:根据题意,得OA=12,OC=4.
所以抛物线的顶点横坐标为6,即﹣==6,∴b=2,
∵C(0,4),∴c=4,
所以抛物线解析式为:y=﹣x2+2x+4=﹣(x﹣6)2+10
当y=8时,8=﹣(x﹣6)2+10,解得x1=6+2,x2=6﹣2.
则x1﹣x2=4.所以两排灯的水平距离最小是4.故选:D.
5、广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠和喷头的水平距离x(米)的函数解析式是y=x2+6x(0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是( )
A.1米
B.2米
C.5米
D.6米
【解答】解:方法一:
根据题意,得y=x2+6x(0≤x≤4)=﹣(x﹣2)2+6
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
方法二:因为对称轴x==2,
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
故选:B.
6、某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价为偶数提高(
)
A.
8元或10元
B.
12元
C.
8元
D.
10元
解:依题意,得
,,
抛物线开口向下,函数有最大值,
即当时,y的最大值为605,
售价为偶数,为18或20,
当时,,
当时,,
为18或20时y的值相同,
商品提高了元或元,
故选A.
7、用长为12
m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,垂足分别为A,B,∠C=∠D=∠E.设CD=DE=x
m,五边形ABCDE的面积为S
m2,则S的最大值为( )
A.12
B.12
C.24
D.没有最大值
[解析]
连接EC,过点D作DF⊥EC,垂足为F.
∵∠DCB=∠CDE=∠DEA,∠EAB=∠CBA=90°,∴∠DCB=∠CDE=∠DEA=120°.
∵DE=CD,∴∠DEC=∠DCE=30°,∴∠CEA=∠ECB=90°,∴四边形EABC为矩形.
∵DE=x
m,∴AE=(6-x)m,DF=x
m,EC=x
m,
∴S=·x·x+(6-x)·x=-x2+6
x(0.
故选A
8、如图,将一个小球从斜坡上的点O处抛出,小球的抛出路线可以用二次函数y=4x-x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5
m时,小球距点O的水平距离为3
m
B.小球距点O的水平距离超过4
m后呈下降趋势
C.小球落地点距点O的水平距离为7
m
D.小球距点O的水平距离为2.5
m和5.5
m时的高度相同
[解析]
令y=7.5,得4x-x2=7.5.解得x1=3,x2=5.可见选项A错误.
由y=4x-x2得y=-(x-4)2+8,∴对称轴为直线x=4,当x>4时,y随x的增大而减小,选项B正确.
联立y=4x-x2与y=x,解得或∴抛物线与直线的交点坐标为(0,0),,可见选项C正确.
由对称性可知选项D正确.
综上所述,只有选项A中的结论是错误的,故选A.
9、如图是抛物线形拱桥的剖面图,拱底宽12m,拱高8m,
设计警戒水位为6m,当拱桥内水位达到警戒水位时,拱桥内的水面宽度是(
)
A.
3m
B.
6m
C.
D.
解:如图建立直角坐标系,
设抛物线的解析式为,
由题意,得解得?;
当时,即,解得:,
拱桥内的水面宽度,
故选B.
10、从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.有下列结论:①小球在空中经过的路程是40
m;②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;④小球的高度h=30
m时,t=1.5
s.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②③
[解析]
①由图象知小球在空中达到的最大高度是40
m,故①错误;
②小球抛出3秒后,速度越来越快,故②正确;
③∵小球抛出3秒时达到最高点,∴速度为0,故③正确;
④设函数解析式为h=a(t-3)2+40,
把O(0,0)代入得0=a(0-3)2+40.解得a=-,
∴函数解析式为h=-(t-3)2+40.
把h=30代入解析式,得30=-(t-3)2+40,
解得t=4.5或t=1.5,
∴小球的高度h=30
m时,t=1.5
s或4.5
s,故④错误.
故选D.
二、填空题
11、已知一个直角三角形两直角边之和为20
cm,则这个直角三角形的最大面积为( B )
(A)25
cm2
(B)50
cm2
(C)100
cm2
(D)不确定
12、如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900
m(篱笆的厚度忽略不计),当AB=________m时,矩形ABCD的面积最大.
[解析]
设AB=x
m,则AB=EF=CD=x
m,所以AD=BC=(900-3x)m.设矩形ABCD的面积为y
m2,
则y=x·(900-3x)=-x2+450x(0<x<300).由于二次项系数小于0,
所以y有最大值,且当x=-=-=150时,函数y取得最大值.
故当AB=150
m矩形ABCD的面积最大.
13、航天飞机从某个时间t秒开始,其飞行高度为h=﹣10t2+700t+21000(单位:英尺),对人而言不低于31000英尺时会感觉到失重,则整个过程中能体会到失重感觉的时间为 秒.
【解答】解:依题意,得:﹣10t2+700t+21000=31000,
解得:t1=20,t2=50,
∴整个过程中能体会到失重感觉的时间为50﹣20=30(秒).
故答案为:30.
14、如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽AB=1.6m时,涵洞顶点与水面的距离是2.4m.这时,离开水面1.5m处,涵洞的宽DE为 .
【解答】解:∵抛物线y=ax2(a<0),
点B在抛物线上,将B(0.8,﹣2.4),
它的坐标代入y=ax2(a<0),求得a=﹣,
所求解析式为y=﹣x2.再由条件设D点坐标为(x,﹣0.9),
则有:﹣0.9=﹣x2.,解得:x=±,所以宽度为,
故答案为:.
15、某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1
m宽的门.已知计划中的材料可建墙体总长为27
m,则能建成的饲养室总占地面积最大为________m2.
[解析]
设与墙垂直的一边的长为x
m,则与墙平行的一边的长为27-(3x-1)+2=(30-3x)m.因此饲养室总占地面积S=x(30-3x)=-3x2+30x,
∴当x=-=5时,S最大,S最大值=-3×52+30×5=75.
故能建成的饲养室总占地面积最大为75
m2.
16、某公园有一个圆形喷水池,喷出的水流呈抛物线,水流的高度h(单位:m)与水流喷出时间t(单位:s)之间的关系式为h=30t﹣5t2,那么水流从喷出至回落到水池所需要的时间是 s.
【解答】解:∵h=30t﹣5t2,
∴当h=0时,t=0或t=6,
∴水流从喷出至回落到水池所需要的时间是:6﹣0=6,
故答案为:6.
17、如图是某地一座抛物线形拱桥,桥拱在竖直平面内与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9
m,AB=36
m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7
m,则DE的长为________m.
[解析]
建立如图所示的平面直角坐标系,设AB与y轴交于点H.
∵AB=36
m,∴AH=BH=18
m.
由题可知:OH=7
m,CH=9
m,∴OC=9+7=16(m).
设该抛物线的解析式为y=ax2+k.
∵抛物线的顶点为C(0,16),∴抛物线的解析式为y=ax2+16.
把(18,7)代入解析式,得7=18×18a+16,∴7=324a+16,∴a=-,∴y=-x2+16.
当y=0时,0=-x2+16,∴-x2=-16,解得x=±24,∴E(24,0),D(-24,0),
∴OE=OD=24
m,∴DE=OD+OE=24+24=48(m).
18、铅球行进高度y(m)与水平距离x(m)之间的关系为y=﹣x2+x+,铅球推出后最大高度是 m,铅球落地时的水平距离是 m.
【解答】解:∵y=﹣x2+x+,∴y=﹣(x﹣4)2+3
因为﹣<0,所以当x=4时,y有最大值为3.
所以铅球推出后最大高度是3m.令y=0,即0=﹣(x﹣4)2+3
解得x1=10,x2=﹣2(舍去),所以铅球落地时的水平距离是10m.
故答案为3、10.
三、解答题
19、如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-x+3x+1的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
解:(1)y=-x2+3x+1=-(x-)2+,
所以当x=时,y有最大值,
所以演员弹跳离地面的最大高度是4.75米.
(2)能表演成功.理由如下:
当x=4时,y=-×42+3×4+1=-9.6+13=3.4,
即点B(4,3.4)在抛物线y=-x2+3x+1上,
所以能表演成功.
20、如图,已知A,B,C,D为矩形的四个顶点,AB=16
cm,AD=6
cm,动点P,Q分别从点A,C同时出发,点P以3
cm/s的速度向点B移动,点Q以2
cm/s的速度向点D移动,当其中一点到达终点时,另一点也随之停止移动.
(1)经过几秒,P,Q两点之间的距离是10
cm?
(2)P,Q两点之间的距离何时最小?
解:(1)设经过x
s,P,Q两点之间的距离是10
cm,
则AP=3x,CQ=2x,过点Q作QM⊥AB于点M,
则PM=|16-2x-3x|=|16-5x|.
根据勾股定理,得PM2+QM2=PQ2,即(16-5x)2+62=102,
解得x1=1.6,x2=4.8.
答:经过1.6
s或4.8
s,P,Q两点之间的距离是10
cm.
(2)∵PQ=,
∴当16-5x=0,即x=时,PQ最小.
故当点P,Q出发
s时,PQ最小.
21、一自动喷灌设备的喷流情况如图所示,设水管AB在高出地面1.5米的B处有一自动旋转的喷水头,一瞬间喷出的水流是抛物线状,喷头B与水流最高点C的连线成45°角,水流最高点C比喷头高2米,
求:(1)点C的坐标;(2)此抛物线的解析式;(3)水流落点D到点A的距离.
解:(1)过点C作CE⊥y轴于点E,CF⊥x轴于点F,则∠CBE=45°,∴EC=EB=2米.
∵AB=1.5米,∴CF=AE=AB+BE=1.5+2=3.5(米),∴C(2,3.5).
(2)设抛物线的解析式为y=a(x-2)2+3.5.
∵抛物线过点B(0,1.5),∴1.5=a(0-2)2+3.5,∴a=-,
∴y=-(x-2)2+3.5=-x2+2x+.
(3)∵抛物线与x轴相交时,y=0,∴0=-x2+2x+,即x2-4x-3=0,
解得x1=2+,x2=2-(舍去),∴AD=2+,即水流落点D到点A的距离为(2+)米.
22、如图所示,隧道的截面由抛物线和长方形构成,长方形的长是12
m,宽是4
m.按照图中所示的直角坐标系,抛物线可以用
y=x+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3
m时,到地面OA的距离为m.
(1)求该抛物线的函数解析式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6
m,宽为4
m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8
m,那么两排灯的水平距离最小是多少?
解:(1)由题意,知点B,C,B1的坐标分别为(0,4),(3,),(12,4),
把B(0,4),C(3,)代入y=x+bx+c,得解得
所以该抛物线的函数解析式为y=-x+2x+4.
因为y=-x+2x+4=(x-6)+10,
所以点D的坐标为(6,10),
所以拱顶D到地面OA的距离为10
m.
(2)这辆货车能安全通过.理由如下:
由题意得,货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y=>6,
所以这辆货车能安全通过.
(3)把y=8代入y=-x2+2x+4,得8=-x2+2x+4,
解得x1=6+2,x2=6-2,
则x1-x2=4.
所以两排灯的水平距离最小是4
m.
复习
-苏科版九年级数学下册
巩固训练
一、选择题
1、如图,利用一面墙,其他三边用80米长的篱笆围成一块矩形场地,墙长为30米,则围成矩形场地的最大面积为( )
A.800平方米
B.750平方米
C.600平方米
D.2400平方米
2、小敏用一根长为8
cm的细铁丝围成矩形,则矩形的最大面积是( )
A.4
cm2
B.8
cm2
C.16
cm2
D.32
cm2
3、小敏在某次投篮中,球的运动线路是抛物线y=-x2+3.5的一部分(如图5-5-5).若命中篮圈中心,则他与篮底的距离l是( )
A.3.5
m
B.4
m
C.4.5
m
D.4.6
m
4、如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m
B.4m
C.4
m
D.4m
5、广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠和喷头的水平距离x(米)的函数解析式是y=x2+6x(0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是( )
A.1米
B.2米
C.5米
D.6米
6、某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价为偶数提高(
)
A.
8元或10元
B.
12元
C.
8元
D.
10元
7、用长为12
m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,垂足分别为A,B,∠C=∠D=∠E.设CD=DE=x
m,五边形ABCDE的面积为S
m2,则S的最大值为( )
A.12
B.12
C.24
D.没有最大值
8、如图,将一个小球从斜坡上的点O处抛出,小球的抛出路线可以用二次函数y=4x-x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5
m时,小球距点O的水平距离为3
m
B.小球距点O的水平距离超过4
m后呈下降趋势
C.小球落地点距点O的水平距离为7
m
D.小球距点O的水平距离为2.5
m和5.5
m时的高度相同
9、如图是抛物线形拱桥的剖面图,拱底宽12m,拱高8m,
设计警戒水位为6m,当拱桥内水位达到警戒水位时,拱桥内的水面宽度是(
)
A.
3m
B.
6m
C.
D.
10、从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.有下列结论:①小球在空中经过的路程是40
m;②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;④小球的高度h=30
m时,t=1.5
s.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②③
二、填空题
11、已知一个直角三角形两直角边之和为20
cm,则这个直角三角形的最大面积为________
12、如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900
m(篱笆的厚度忽略不计),当AB=________m时,矩形ABCD的面积最大.
13、航天飞机从某个时间t秒开始,其飞行高度为h=﹣10t2+700t+21000(单位:英尺),对人而言不低于31000英尺时会感觉到失重,则整个过程中能体会到失重感觉的时间为 秒.
14、如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽AB=1.6m时,涵洞顶点与水面的距离是2.4m.这时,离开水面1.5m处,涵洞的宽DE为 .
15、某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1
m宽的门.已知计划中的材料可建墙体总长为27
m,则能建成的饲养室总占地面积最大为________m2.
16、某公园有一个圆形喷水池,喷出的水流呈抛物线,水流的高度h(单位:m)与水流喷出时间t(单位:s)之间的关系式为h=30t﹣5t2,那么水流从喷出至回落到水池所需要的时间是 s.
17、如图是某地一座抛物线形拱桥,桥拱在竖直平面内与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9
m,AB=36
m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7
m,则DE的长为________m.
18、铅球行进高度y(m)与水平距离x(m)之间的关系为y=﹣x2+x+,铅球推出后最大高度是 m,铅球落地时的水平距离是 m.
三、解答题
19、如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-x+3x+1的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
20、如图,已知A,B,C,D为矩形的四个顶点,AB=16
cm,AD=6
cm,动点P,Q分别从点A,C同时出发,点P以3
cm/s的速度向点B移动,点Q以2
cm/s的速度向点D移动,当其中一点到达终点时,另一点也随之停止移动.
(1)经过几秒,P,Q两点之间的距离是10
cm?
(2)P,Q两点之间的距离何时最小?
21、一自动喷灌设备的喷流情况如图所示,设水管AB在高出地面1.5米的B处有一自动旋转的喷水头,一瞬间喷出的水流是抛物线状,喷头B与水流最高点C的连线成45°角,水流最高点C比喷头高2米,
求:(1)点C的坐标;(2)此抛物线的解析式;(3)水流落点D到点A的距离.
22、如图所示,隧道的截面由抛物线和长方形构成,长方形的长是12
m,宽是4
m.按照图中所示的直角坐标系,抛物线可以用
y=x+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3
m时,到地面OA的距离为m.
(1)求该抛物线的函数解析式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6
m,宽为4
m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8
m,那么两排灯的水平距离最小是多少?
5.5用二次函数解决问题
复习
-苏科版九年级数学下册
巩固训练(答案)
一、选择题
1、如图,利用一面墙,其他三边用80米长的篱笆围成一块矩形场地,墙长为30米,则围成矩形场地的最大面积为( )
A.800平方米
B.750平方米
C.600平方米
D.2400平方米
[解析]
设矩形场地中平行于墙的边长为x米,则垂直于墙的边长为米,
围成矩形场地的面积为y平方米,
则y=x·=-x2+40x=-(x-40)2+800.
∵a<0,∴x<40时,y随x的增大而增大,由于墙长为30米,∴0
故选B
2、小敏用一根长为8
cm的细铁丝围成矩形,则矩形的最大面积是( A )
A.4
cm2
B.8
cm2
C.16
cm2
D.32
cm2
[解析]
设矩形的一边长为x
cm,则另一边长为cm,
故矩形的面积S=x=-x2+4x=-(x-2)2+4,所
以当x=2时,S最大值=4.故矩形的最大面积为4
cm2.
3、小敏在某次投篮中,球的运动线路是抛物线y=-x2+3.5的一部分(如图5-5-5).若命中篮圈中心,则他与篮底的距离l是( )
A.3.5
m
B.4
m
C.4.5
m
D.4.6
m
[解析]
当y=3.05时,-x2+3.5=3.05,解得x1=-1.5(舍去),x2=1.5,
∴l=2.5+1.5=4(m).
故选B.
4、如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m
B.4m
C.4
m
D.4m
【解答】解:根据题意,得OA=12,OC=4.
所以抛物线的顶点横坐标为6,即﹣==6,∴b=2,
∵C(0,4),∴c=4,
所以抛物线解析式为:y=﹣x2+2x+4=﹣(x﹣6)2+10
当y=8时,8=﹣(x﹣6)2+10,解得x1=6+2,x2=6﹣2.
则x1﹣x2=4.所以两排灯的水平距离最小是4.故选:D.
5、广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠和喷头的水平距离x(米)的函数解析式是y=x2+6x(0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是( )
A.1米
B.2米
C.5米
D.6米
【解答】解:方法一:
根据题意,得y=x2+6x(0≤x≤4)=﹣(x﹣2)2+6
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
方法二:因为对称轴x==2,
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
故选:B.
6、某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价为偶数提高(
)
A.
8元或10元
B.
12元
C.
8元
D.
10元
解:依题意,得
,,
抛物线开口向下,函数有最大值,
即当时,y的最大值为605,
售价为偶数,为18或20,
当时,,
当时,,
为18或20时y的值相同,
商品提高了元或元,
故选A.
7、用长为12
m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,垂足分别为A,B,∠C=∠D=∠E.设CD=DE=x
m,五边形ABCDE的面积为S
m2,则S的最大值为( )
A.12
B.12
C.24
D.没有最大值
[解析]
连接EC,过点D作DF⊥EC,垂足为F.
∵∠DCB=∠CDE=∠DEA,∠EAB=∠CBA=90°,∴∠DCB=∠CDE=∠DEA=120°.
∵DE=CD,∴∠DEC=∠DCE=30°,∴∠CEA=∠ECB=90°,∴四边形EABC为矩形.
∵DE=x
m,∴AE=(6-x)m,DF=x
m,EC=x
m,
∴S=·x·x+(6-x)·x=-x2+6
x(0
故选A
8、如图,将一个小球从斜坡上的点O处抛出,小球的抛出路线可以用二次函数y=4x-x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5
m时,小球距点O的水平距离为3
m
B.小球距点O的水平距离超过4
m后呈下降趋势
C.小球落地点距点O的水平距离为7
m
D.小球距点O的水平距离为2.5
m和5.5
m时的高度相同
[解析]
令y=7.5,得4x-x2=7.5.解得x1=3,x2=5.可见选项A错误.
由y=4x-x2得y=-(x-4)2+8,∴对称轴为直线x=4,当x>4时,y随x的增大而减小,选项B正确.
联立y=4x-x2与y=x,解得或∴抛物线与直线的交点坐标为(0,0),,可见选项C正确.
由对称性可知选项D正确.
综上所述,只有选项A中的结论是错误的,故选A.
9、如图是抛物线形拱桥的剖面图,拱底宽12m,拱高8m,
设计警戒水位为6m,当拱桥内水位达到警戒水位时,拱桥内的水面宽度是(
)
A.
3m
B.
6m
C.
D.
解:如图建立直角坐标系,
设抛物线的解析式为,
由题意,得解得?;
当时,即,解得:,
拱桥内的水面宽度,
故选B.
10、从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.有下列结论:①小球在空中经过的路程是40
m;②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;④小球的高度h=30
m时,t=1.5
s.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②③
[解析]
①由图象知小球在空中达到的最大高度是40
m,故①错误;
②小球抛出3秒后,速度越来越快,故②正确;
③∵小球抛出3秒时达到最高点,∴速度为0,故③正确;
④设函数解析式为h=a(t-3)2+40,
把O(0,0)代入得0=a(0-3)2+40.解得a=-,
∴函数解析式为h=-(t-3)2+40.
把h=30代入解析式,得30=-(t-3)2+40,
解得t=4.5或t=1.5,
∴小球的高度h=30
m时,t=1.5
s或4.5
s,故④错误.
故选D.
二、填空题
11、已知一个直角三角形两直角边之和为20
cm,则这个直角三角形的最大面积为( B )
(A)25
cm2
(B)50
cm2
(C)100
cm2
(D)不确定
12、如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900
m(篱笆的厚度忽略不计),当AB=________m时,矩形ABCD的面积最大.
[解析]
设AB=x
m,则AB=EF=CD=x
m,所以AD=BC=(900-3x)m.设矩形ABCD的面积为y
m2,
则y=x·(900-3x)=-x2+450x(0<x<300).由于二次项系数小于0,
所以y有最大值,且当x=-=-=150时,函数y取得最大值.
故当AB=150
m矩形ABCD的面积最大.
13、航天飞机从某个时间t秒开始,其飞行高度为h=﹣10t2+700t+21000(单位:英尺),对人而言不低于31000英尺时会感觉到失重,则整个过程中能体会到失重感觉的时间为 秒.
【解答】解:依题意,得:﹣10t2+700t+21000=31000,
解得:t1=20,t2=50,
∴整个过程中能体会到失重感觉的时间为50﹣20=30(秒).
故答案为:30.
14、如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽AB=1.6m时,涵洞顶点与水面的距离是2.4m.这时,离开水面1.5m处,涵洞的宽DE为 .
【解答】解:∵抛物线y=ax2(a<0),
点B在抛物线上,将B(0.8,﹣2.4),
它的坐标代入y=ax2(a<0),求得a=﹣,
所求解析式为y=﹣x2.再由条件设D点坐标为(x,﹣0.9),
则有:﹣0.9=﹣x2.,解得:x=±,所以宽度为,
故答案为:.
15、某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1
m宽的门.已知计划中的材料可建墙体总长为27
m,则能建成的饲养室总占地面积最大为________m2.
[解析]
设与墙垂直的一边的长为x
m,则与墙平行的一边的长为27-(3x-1)+2=(30-3x)m.因此饲养室总占地面积S=x(30-3x)=-3x2+30x,
∴当x=-=5时,S最大,S最大值=-3×52+30×5=75.
故能建成的饲养室总占地面积最大为75
m2.
16、某公园有一个圆形喷水池,喷出的水流呈抛物线,水流的高度h(单位:m)与水流喷出时间t(单位:s)之间的关系式为h=30t﹣5t2,那么水流从喷出至回落到水池所需要的时间是 s.
【解答】解:∵h=30t﹣5t2,
∴当h=0时,t=0或t=6,
∴水流从喷出至回落到水池所需要的时间是:6﹣0=6,
故答案为:6.
17、如图是某地一座抛物线形拱桥,桥拱在竖直平面内与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9
m,AB=36
m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7
m,则DE的长为________m.
[解析]
建立如图所示的平面直角坐标系,设AB与y轴交于点H.
∵AB=36
m,∴AH=BH=18
m.
由题可知:OH=7
m,CH=9
m,∴OC=9+7=16(m).
设该抛物线的解析式为y=ax2+k.
∵抛物线的顶点为C(0,16),∴抛物线的解析式为y=ax2+16.
把(18,7)代入解析式,得7=18×18a+16,∴7=324a+16,∴a=-,∴y=-x2+16.
当y=0时,0=-x2+16,∴-x2=-16,解得x=±24,∴E(24,0),D(-24,0),
∴OE=OD=24
m,∴DE=OD+OE=24+24=48(m).
18、铅球行进高度y(m)与水平距离x(m)之间的关系为y=﹣x2+x+,铅球推出后最大高度是 m,铅球落地时的水平距离是 m.
【解答】解:∵y=﹣x2+x+,∴y=﹣(x﹣4)2+3
因为﹣<0,所以当x=4时,y有最大值为3.
所以铅球推出后最大高度是3m.令y=0,即0=﹣(x﹣4)2+3
解得x1=10,x2=﹣2(舍去),所以铅球落地时的水平距离是10m.
故答案为3、10.
三、解答题
19、如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-x+3x+1的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
解:(1)y=-x2+3x+1=-(x-)2+,
所以当x=时,y有最大值,
所以演员弹跳离地面的最大高度是4.75米.
(2)能表演成功.理由如下:
当x=4时,y=-×42+3×4+1=-9.6+13=3.4,
即点B(4,3.4)在抛物线y=-x2+3x+1上,
所以能表演成功.
20、如图,已知A,B,C,D为矩形的四个顶点,AB=16
cm,AD=6
cm,动点P,Q分别从点A,C同时出发,点P以3
cm/s的速度向点B移动,点Q以2
cm/s的速度向点D移动,当其中一点到达终点时,另一点也随之停止移动.
(1)经过几秒,P,Q两点之间的距离是10
cm?
(2)P,Q两点之间的距离何时最小?
解:(1)设经过x
s,P,Q两点之间的距离是10
cm,
则AP=3x,CQ=2x,过点Q作QM⊥AB于点M,
则PM=|16-2x-3x|=|16-5x|.
根据勾股定理,得PM2+QM2=PQ2,即(16-5x)2+62=102,
解得x1=1.6,x2=4.8.
答:经过1.6
s或4.8
s,P,Q两点之间的距离是10
cm.
(2)∵PQ=,
∴当16-5x=0,即x=时,PQ最小.
故当点P,Q出发
s时,PQ最小.
21、一自动喷灌设备的喷流情况如图所示,设水管AB在高出地面1.5米的B处有一自动旋转的喷水头,一瞬间喷出的水流是抛物线状,喷头B与水流最高点C的连线成45°角,水流最高点C比喷头高2米,
求:(1)点C的坐标;(2)此抛物线的解析式;(3)水流落点D到点A的距离.
解:(1)过点C作CE⊥y轴于点E,CF⊥x轴于点F,则∠CBE=45°,∴EC=EB=2米.
∵AB=1.5米,∴CF=AE=AB+BE=1.5+2=3.5(米),∴C(2,3.5).
(2)设抛物线的解析式为y=a(x-2)2+3.5.
∵抛物线过点B(0,1.5),∴1.5=a(0-2)2+3.5,∴a=-,
∴y=-(x-2)2+3.5=-x2+2x+.
(3)∵抛物线与x轴相交时,y=0,∴0=-x2+2x+,即x2-4x-3=0,
解得x1=2+,x2=2-(舍去),∴AD=2+,即水流落点D到点A的距离为(2+)米.
22、如图所示,隧道的截面由抛物线和长方形构成,长方形的长是12
m,宽是4
m.按照图中所示的直角坐标系,抛物线可以用
y=x+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3
m时,到地面OA的距离为m.
(1)求该抛物线的函数解析式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6
m,宽为4
m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8
m,那么两排灯的水平距离最小是多少?
解:(1)由题意,知点B,C,B1的坐标分别为(0,4),(3,),(12,4),
把B(0,4),C(3,)代入y=x+bx+c,得解得
所以该抛物线的函数解析式为y=-x+2x+4.
因为y=-x+2x+4=(x-6)+10,
所以点D的坐标为(6,10),
所以拱顶D到地面OA的距离为10
m.
(2)这辆货车能安全通过.理由如下:
由题意得,货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y=>6,
所以这辆货车能安全通过.
(3)把y=8代入y=-x2+2x+4,得8=-x2+2x+4,
解得x1=6+2,x2=6-2,
则x1-x2=4.
所以两排灯的水平距离最小是4
m.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
