2020-2021学年冀教新版九年级上册数学《第25章 图形的相似》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年冀教新版九年级上册数学《第25章 图形的相似》单元测试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 467.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 00:00:00 | ||
图片预览



文档简介
2020-2021学年冀教新版九年级上册数学《第25章
图形的相似》单元测试卷
一.选择题
1.如果4x﹣5y=0,那么的值是( )
A.
B.
C.
D.4
2.如图,在△ABC中,DE∥BC,,则下列结论中正确的是( )
A.
B.
C.
D.
3.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,光源到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.21cm
B.14cm
C.6cm
D.24cm
4.等边三角形OAB在平面直角坐标系中的位置如图所示,已知△OAB边长为6,且△OAB与△OA′B′关点O成位似图形,且位似比为1:2,则点A′的坐标可能是( )
A.(﹣6,6)
B.(6,6)
C.(﹣3,﹣3)
D.(6,﹣6)
5.如图,点D、E分别在△ABC的边AB、BC上,下列条件中,不能判定DE∥AC的条件是( )
A.
B.
C.
D.
6.两个相似三角形面积比是4:9,其中一个三角形的周长为24cm,则另一个三角形的周长是( )cm.
A.16
B.16或28
C.36
D.16或36
7.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A.
B.
C.﹣1
D.﹣1
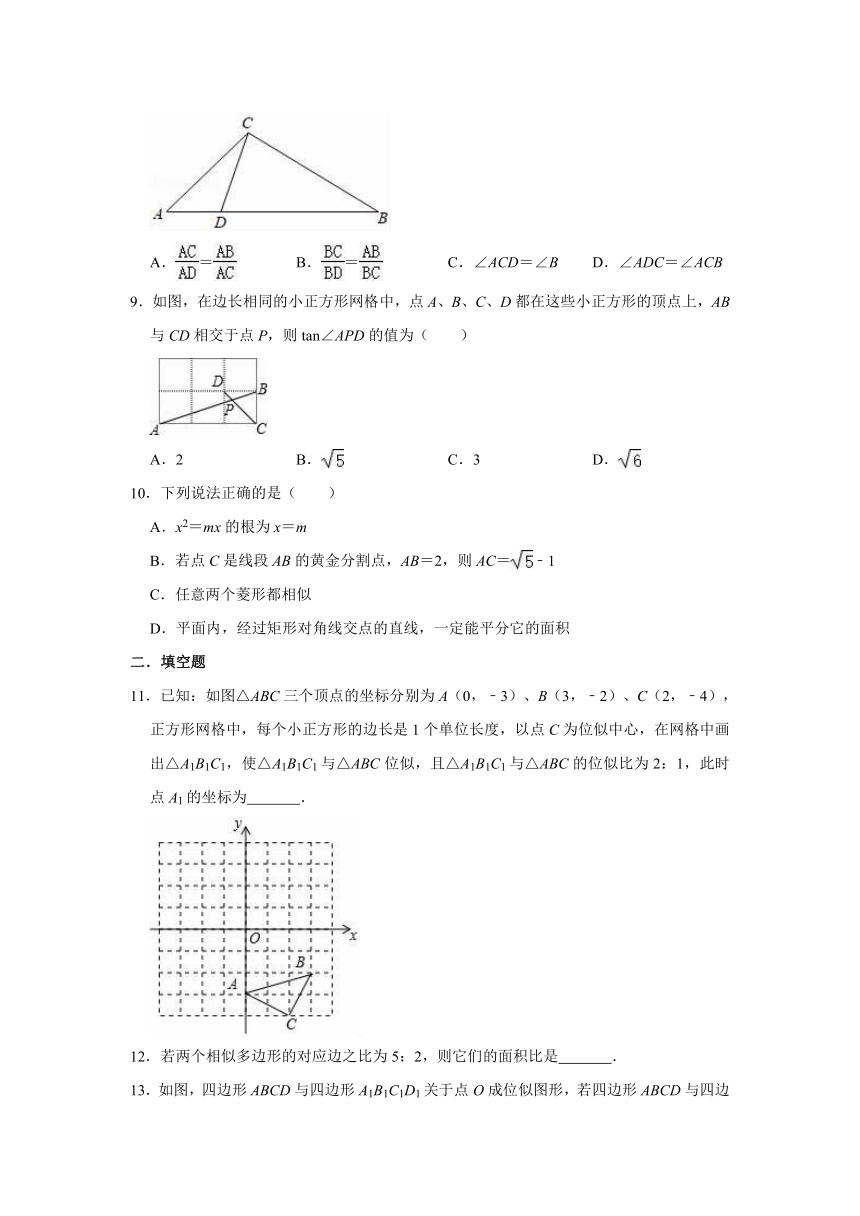
8.如图,下列选项中不能判定△ACD∽△ABC的是( )
A.=
B.=
C.∠ACD=∠B
D.∠ADC=∠ACB
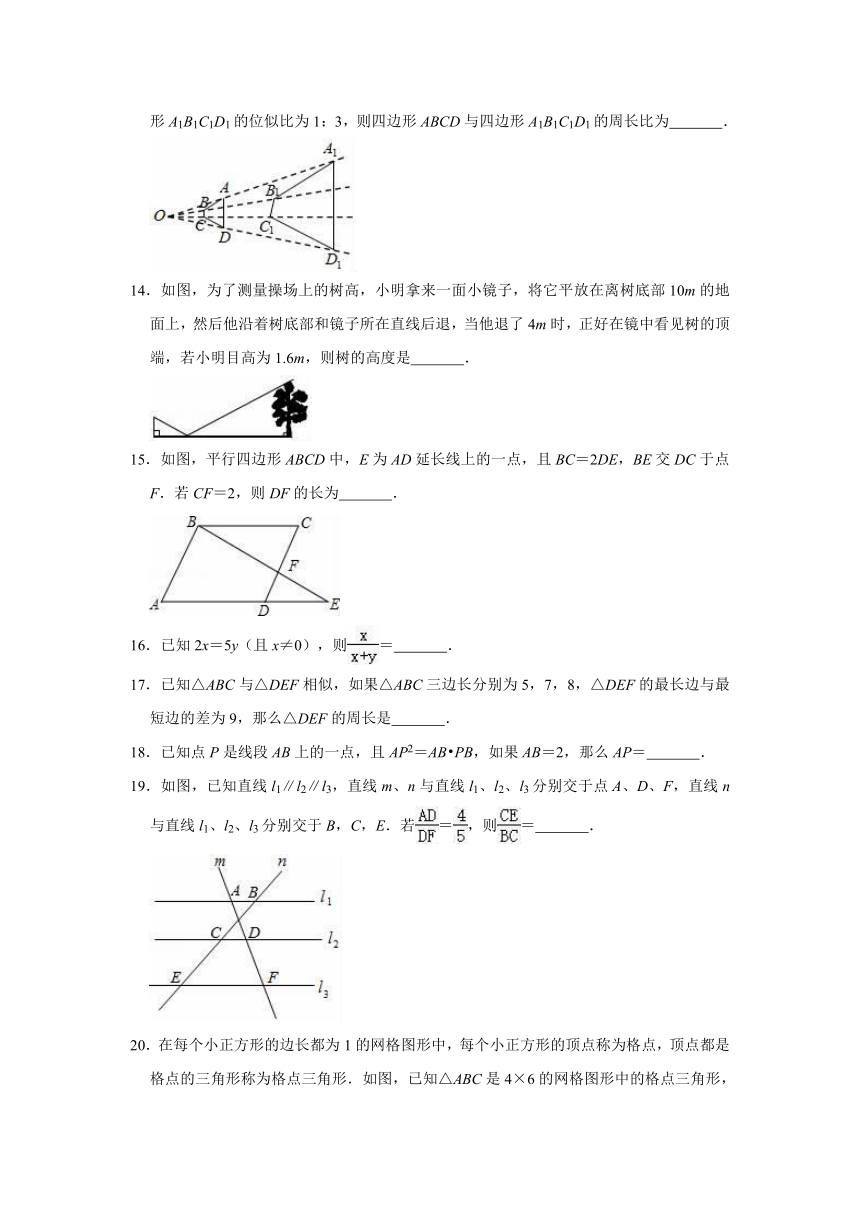
9.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为( )
A.2
B.
C.3
D.
10.下列说法正确的是( )
A.x2=mx的根为x=m
B.若点C是线段AB的黄金分割点,AB=2,则AC=﹣1
C.任意两个菱形都相似
D.平面内,经过矩形对角线交点的直线,一定能平分它的面积
二.填空题
11.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,此时点A1的坐标为
.
12.若两个相似多边形的对应边之比为5:2,则它们的面积比是
.
13.如图,四边形ABCD与四边形A1B1C1D1关于点O成位似图形,若四边形ABCD与四边形A1B1C1D1的位似比为1:3,则四边形ABCD与四边形A1B1C1D1的周长比为
.
14.如图,为了测量操场上的树高,小明拿来一面小镜子,将它平放在离树底部10m的地面上,然后他沿着树底部和镜子所在直线后退,当他退了4m时,正好在镜中看见树的顶端,若小明目高为1.6m,则树的高度是
.
15.如图,平行四边形ABCD中,E为AD延长线上的一点,且BC=2DE,BE交DC于点F.若CF=2,则DF的长为
.
16.已知2x=5y(且x≠0),则=
.
17.已知△ABC与△DEF相似,如果△ABC三边长分别为5,7,8,△DEF的最长边与最短边的差为9,那么△DEF的周长是
.
18.已知点P是线段AB上的一点,且AP2=AB?PB,如果AB=2,那么AP=
.
19.如图,已知直线l1∥l2∥l3,直线m、n与直线l1、l2、l3分别交于点A、D、F,直线n与直线l1、l2、l3分别交于B,C,E.若=,则=
.
20.在每个小正方形的边长都为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知△ABC是4×6的网格图形中的格点三角形,则该图中所有与△ABC相似的格点三角形中,最大的三角形面积是
.
三.解答题
21.在一张比例尺为1:20的地图上,有一块多边形区域的周长是24cm,面积是20cm2,求这个区域的实际周长和面积.
22.已知a:b:c=2:3:4,且a+3b﹣2c=15,求a+b﹣c的值.
23.如图,点R是正方形ABCD的边AB边上的黄金分割点,且AR>RB,S1表示AR为边长的正方形面积,S2表示以BC为长,BR为宽的矩形面积,S3表示正方形ABCD除去S1和S2剩余的面积,求S3:S2的值.
24.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设=,AD=12,求线段BD的长.
25.20世纪90年代以来,我国户外广告行业取得了突飞猛进的发展,户外广告装置多设立于城市道路、铁路、公路等主要交通干道边上,面向密集的车流和人流.某天,小芳走到如图所示的C处时,看到正对面一条东西走向的笔直公路.上有一辆汽车从东面驶来,到达Q处时,恰好被公路北侧边上竖着的一个长12m的广告牌AB挡住,3s后在P处又重新看到该汽车的全部车身,已知该汽车的行驶速度是21.6km/h,假设AB∥PQ,公路宽为10m,求小芳所在C处到公路南侧PQ的距离.
26.如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
27.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点)和点O,按要求在网格内画出下列图形.
(1)以D为旋转中心,将四边形ABCD逆时针旋转90°,得到四边形A1B1C1D1;
(2)以O为位似中心,将四边形ABCD作位似变换,使放大前后的面积之比为1:4,得到四边形A2B2C2D2.
参考答案与试题解析
一.选择题
1.解:∵4x﹣5y=0,
∴=,
∴=﹣1=﹣1=;
故选:C.
2.解:∵=,
∴=,
∵DE∥BC,
∴△ADE∽△ABC,==,所以B选项的结论错误;
∴==,所以A选项的结论错误;
==,所以C选项的结论正确;
=()2=,所以D选项的结论错误.
故选:C.
3.解:如图所示,∵DE∥BC,
∴△AED∽△ABC,
∴=,
设屏幕上的图形高是xcm,则=,
解得:x=21.
答:屏幕上图形的高度为21cm,
故选:A.
4.解:作AC⊥OB于C,
∵△OAB为等边三角形,AC⊥OB,
∴OC=OB=3,
∴AC==3,
∴点A的坐标为(3,3),
∵△OAB与△OA′B′关点O成位似图形,且位似比为1:2,
∴点A′的坐标为(3×2,3×2)或(﹣3×2,﹣3×2),即(6,6)或(﹣6,﹣6),
故选:B.
5.解:A、∵,不能判定DE∥AC,选项符合题意;
B、∵,∴DE∥AC,选项不符合题意;
C、∵,∴,∴DE∥AC,选项不符合题意;
D、∵,∴,∴DE∥AC,选项不符合题意;
故选:A.
6.解:∵两个相似三角形面积比是4:9,
∴两个相似三角形相似比是2:3,
∴两个相似三角形周长比是2:3,
∵一个三角形的周长为24cm,
∴另一个三角形的周长是16cm或36cm,
故选:D.
7.解:在Rt△OAB中,∠OAB=90°,AB=1,OA=2,由勾股定理得:OB==,
∵BC=AB,AB=1,
∴BC=1,
∴OC=OB﹣BC=﹣1,
即OP=﹣1,
∵OP的中点是D,
∴OD=OP=×(﹣1)=,
即点D表示的数是,
故选:A.
8.解:A、根据两边成比例夹角相等,可以证明三角形相似,本选项不符合题意.
B、无法判断三角形相似,本选项符合题意.
C、根据两角对应相等的两个三角形相似,可以判断两个三角形相似,本选项不符合题意.
D、根据两角对应相等的两个三角形相似,可以判断两个三角形相似,本选项不符合题意.
故选:B.
9.解:如图:连接BE,
,
∵四边形BCED是正方形,
∴DF=CF=CD,BF=BE,CD=BE,BE⊥CD,
∴BF=CF,
根据题意得:AC∥BD,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,
∴DP=PF=CF=BF,
在Rt△PBF中,tan∠BPF==2,
∵∠APD=∠BPF,
∴tan∠APD=2.
故选:A.
10.解:A、x2=mx的根为x=m或x=0,选项错误,不符合题意;
B、若点C是线段AB的黄金分割点(AC>BC),AB=2,则AC=﹣1,选项错误,不符合题意;
C、角不相等,所以任意两个菱形不一定相似,选项错误.不符合题意;
D、平面内,经过矩形对角线交点的直线,一定能平分它的面积,选项正确,符合题意;
故选:D.
二.填空题
11.解:如图,△A1B1C1为所作;点A1的坐标为(﹣2,﹣2).
故答案为(﹣2,﹣2).
12.解:∵两个相似多边形的对应边的比是5:2,
∴这两个多边形的面积比是52:22,
即这两个多边形的面积比是25:4,
故答案为:25:4.
13.解:∵四边形ABCD与四边形A1B1C1D1的位似比为1:3,
∴四边形ABCD与四边形A1B1C1D1的周长比为:1:3.
故答案为:1:3.
14.解:∵∠ABC=∠DBE,∠ACB=∠DEB=90°,
∴△ABC∽△DBE,
∴BC:BE=AC:DE,
即4:10=1.6:DE,
∴DE=4m,
故答案为:4m.
15.解:∵四边形ABCD是平行四边形,
∴BC∥AE,
∴△BCF∽△EDF,
∴,
∴=,
∴DF=1,
故答案为:1.
16.解:∵2x=5y(且x≠0),
∴y=x,
∴==;
故答案为:.
17.解:设△DEF的最长边为x,最短边为y,依题意,则有:
,解得:x=24,y=15;
∴△ABC和△DEF的相似比为1:3,周长比也是1:3;
∵△ABC的周长=5+7+8=20,
∴△DEF的周长为60,
故答案为:60.
18.解:设AP=x,则PB=2﹣x,
由题意,x2=2(2﹣x),
解得x=﹣1或﹣﹣1(舍弃)
故答案为:﹣1.
19.解:∵直线l1∥l2∥l3,
∴,
∴,
故答案为:.
20.解:图中所有与△ABC相似的格点三角形中,最大的△A′B′C′如图所示:
S△A′B′C′=×4×2=4,
故答案为4.
三.解答题
21.解:地图与该地区的实际图形相似,相似比就是比例尺为1:20,周长的比就是相似比,设实际周长是xcm,则
24:x=1:20,
解得:x=480,
面积的比等于相似比的平方,设实际面积是ycm2,则
20:y=(1:20)2,
解得y=8000,
答:这个区域的实际周长480cm,面积8000cm2.
22.解:由题意设a=2k,b=3k,c=4k,
∵a+3b﹣2c=15,
∴2k+9k﹣8k=15,
∴k=5,
∴a=10,b=15,c=20,
∴a+b﹣c
=10+15﹣20
=5.
23.解:如图,设AB=1,
∵点E是正方形ABCD的边AB边上的黄金分割点,且AE>EB,
∴AE=GF=,
∴BE=FH=AB﹣AE=,
∴S3:S2=(GF?FH):(BC?BE)
=(×):(1×)
=.
故答案为:.
24.证明:(1)∵DE∥AC,
∴∠DEB=∠FCE,
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC;
(2)∵EF∥AB,
∴==,
∵DE∥AC,
∴==,
∵AD=12,
∴=,
∴BD=6.
25.解:设小芳所在C处到公路南侧PQ的距离为xm,
21.6km/h=21.6×=6m/s,
∵AB∥PQ,
∴△CAB∽△CPQ,
∴,
∴=,
∴x=30,
∴小芳所在C处到公路南侧PQ的距离为30m.
26.解:(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:;
27.解:(1)如图,四边形A1B1C1D1为所作;
(2)如图,四边形A2B2C2D2为所作.
图形的相似》单元测试卷
一.选择题
1.如果4x﹣5y=0,那么的值是( )
A.
B.
C.
D.4
2.如图,在△ABC中,DE∥BC,,则下列结论中正确的是( )
A.
B.
C.
D.
3.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,光源到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.21cm
B.14cm
C.6cm
D.24cm
4.等边三角形OAB在平面直角坐标系中的位置如图所示,已知△OAB边长为6,且△OAB与△OA′B′关点O成位似图形,且位似比为1:2,则点A′的坐标可能是( )
A.(﹣6,6)
B.(6,6)
C.(﹣3,﹣3)
D.(6,﹣6)
5.如图,点D、E分别在△ABC的边AB、BC上,下列条件中,不能判定DE∥AC的条件是( )
A.
B.
C.
D.
6.两个相似三角形面积比是4:9,其中一个三角形的周长为24cm,则另一个三角形的周长是( )cm.
A.16
B.16或28
C.36
D.16或36
7.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A.
B.
C.﹣1
D.﹣1
8.如图,下列选项中不能判定△ACD∽△ABC的是( )
A.=
B.=
C.∠ACD=∠B
D.∠ADC=∠ACB
9.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为( )
A.2
B.
C.3
D.
10.下列说法正确的是( )
A.x2=mx的根为x=m
B.若点C是线段AB的黄金分割点,AB=2,则AC=﹣1
C.任意两个菱形都相似
D.平面内,经过矩形对角线交点的直线,一定能平分它的面积
二.填空题
11.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,此时点A1的坐标为
.
12.若两个相似多边形的对应边之比为5:2,则它们的面积比是
.
13.如图,四边形ABCD与四边形A1B1C1D1关于点O成位似图形,若四边形ABCD与四边形A1B1C1D1的位似比为1:3,则四边形ABCD与四边形A1B1C1D1的周长比为
.
14.如图,为了测量操场上的树高,小明拿来一面小镜子,将它平放在离树底部10m的地面上,然后他沿着树底部和镜子所在直线后退,当他退了4m时,正好在镜中看见树的顶端,若小明目高为1.6m,则树的高度是
.
15.如图,平行四边形ABCD中,E为AD延长线上的一点,且BC=2DE,BE交DC于点F.若CF=2,则DF的长为
.
16.已知2x=5y(且x≠0),则=
.
17.已知△ABC与△DEF相似,如果△ABC三边长分别为5,7,8,△DEF的最长边与最短边的差为9,那么△DEF的周长是
.
18.已知点P是线段AB上的一点,且AP2=AB?PB,如果AB=2,那么AP=
.
19.如图,已知直线l1∥l2∥l3,直线m、n与直线l1、l2、l3分别交于点A、D、F,直线n与直线l1、l2、l3分别交于B,C,E.若=,则=
.
20.在每个小正方形的边长都为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知△ABC是4×6的网格图形中的格点三角形,则该图中所有与△ABC相似的格点三角形中,最大的三角形面积是
.
三.解答题
21.在一张比例尺为1:20的地图上,有一块多边形区域的周长是24cm,面积是20cm2,求这个区域的实际周长和面积.
22.已知a:b:c=2:3:4,且a+3b﹣2c=15,求a+b﹣c的值.
23.如图,点R是正方形ABCD的边AB边上的黄金分割点,且AR>RB,S1表示AR为边长的正方形面积,S2表示以BC为长,BR为宽的矩形面积,S3表示正方形ABCD除去S1和S2剩余的面积,求S3:S2的值.
24.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设=,AD=12,求线段BD的长.
25.20世纪90年代以来,我国户外广告行业取得了突飞猛进的发展,户外广告装置多设立于城市道路、铁路、公路等主要交通干道边上,面向密集的车流和人流.某天,小芳走到如图所示的C处时,看到正对面一条东西走向的笔直公路.上有一辆汽车从东面驶来,到达Q处时,恰好被公路北侧边上竖着的一个长12m的广告牌AB挡住,3s后在P处又重新看到该汽车的全部车身,已知该汽车的行驶速度是21.6km/h,假设AB∥PQ,公路宽为10m,求小芳所在C处到公路南侧PQ的距离.
26.如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
27.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点)和点O,按要求在网格内画出下列图形.
(1)以D为旋转中心,将四边形ABCD逆时针旋转90°,得到四边形A1B1C1D1;
(2)以O为位似中心,将四边形ABCD作位似变换,使放大前后的面积之比为1:4,得到四边形A2B2C2D2.
参考答案与试题解析
一.选择题
1.解:∵4x﹣5y=0,
∴=,
∴=﹣1=﹣1=;
故选:C.
2.解:∵=,
∴=,
∵DE∥BC,
∴△ADE∽△ABC,==,所以B选项的结论错误;
∴==,所以A选项的结论错误;
==,所以C选项的结论正确;
=()2=,所以D选项的结论错误.
故选:C.
3.解:如图所示,∵DE∥BC,
∴△AED∽△ABC,
∴=,
设屏幕上的图形高是xcm,则=,
解得:x=21.
答:屏幕上图形的高度为21cm,
故选:A.
4.解:作AC⊥OB于C,
∵△OAB为等边三角形,AC⊥OB,
∴OC=OB=3,
∴AC==3,
∴点A的坐标为(3,3),
∵△OAB与△OA′B′关点O成位似图形,且位似比为1:2,
∴点A′的坐标为(3×2,3×2)或(﹣3×2,﹣3×2),即(6,6)或(﹣6,﹣6),
故选:B.
5.解:A、∵,不能判定DE∥AC,选项符合题意;
B、∵,∴DE∥AC,选项不符合题意;
C、∵,∴,∴DE∥AC,选项不符合题意;
D、∵,∴,∴DE∥AC,选项不符合题意;
故选:A.
6.解:∵两个相似三角形面积比是4:9,
∴两个相似三角形相似比是2:3,
∴两个相似三角形周长比是2:3,
∵一个三角形的周长为24cm,
∴另一个三角形的周长是16cm或36cm,
故选:D.
7.解:在Rt△OAB中,∠OAB=90°,AB=1,OA=2,由勾股定理得:OB==,
∵BC=AB,AB=1,
∴BC=1,
∴OC=OB﹣BC=﹣1,
即OP=﹣1,
∵OP的中点是D,
∴OD=OP=×(﹣1)=,
即点D表示的数是,
故选:A.
8.解:A、根据两边成比例夹角相等,可以证明三角形相似,本选项不符合题意.
B、无法判断三角形相似,本选项符合题意.
C、根据两角对应相等的两个三角形相似,可以判断两个三角形相似,本选项不符合题意.
D、根据两角对应相等的两个三角形相似,可以判断两个三角形相似,本选项不符合题意.
故选:B.
9.解:如图:连接BE,
,
∵四边形BCED是正方形,
∴DF=CF=CD,BF=BE,CD=BE,BE⊥CD,
∴BF=CF,
根据题意得:AC∥BD,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,
∴DP=PF=CF=BF,
在Rt△PBF中,tan∠BPF==2,
∵∠APD=∠BPF,
∴tan∠APD=2.
故选:A.
10.解:A、x2=mx的根为x=m或x=0,选项错误,不符合题意;
B、若点C是线段AB的黄金分割点(AC>BC),AB=2,则AC=﹣1,选项错误,不符合题意;
C、角不相等,所以任意两个菱形不一定相似,选项错误.不符合题意;
D、平面内,经过矩形对角线交点的直线,一定能平分它的面积,选项正确,符合题意;
故选:D.
二.填空题
11.解:如图,△A1B1C1为所作;点A1的坐标为(﹣2,﹣2).
故答案为(﹣2,﹣2).
12.解:∵两个相似多边形的对应边的比是5:2,
∴这两个多边形的面积比是52:22,
即这两个多边形的面积比是25:4,
故答案为:25:4.
13.解:∵四边形ABCD与四边形A1B1C1D1的位似比为1:3,
∴四边形ABCD与四边形A1B1C1D1的周长比为:1:3.
故答案为:1:3.
14.解:∵∠ABC=∠DBE,∠ACB=∠DEB=90°,
∴△ABC∽△DBE,
∴BC:BE=AC:DE,
即4:10=1.6:DE,
∴DE=4m,
故答案为:4m.
15.解:∵四边形ABCD是平行四边形,
∴BC∥AE,
∴△BCF∽△EDF,
∴,
∴=,
∴DF=1,
故答案为:1.
16.解:∵2x=5y(且x≠0),
∴y=x,
∴==;
故答案为:.
17.解:设△DEF的最长边为x,最短边为y,依题意,则有:
,解得:x=24,y=15;
∴△ABC和△DEF的相似比为1:3,周长比也是1:3;
∵△ABC的周长=5+7+8=20,
∴△DEF的周长为60,
故答案为:60.
18.解:设AP=x,则PB=2﹣x,
由题意,x2=2(2﹣x),
解得x=﹣1或﹣﹣1(舍弃)
故答案为:﹣1.
19.解:∵直线l1∥l2∥l3,
∴,
∴,
故答案为:.
20.解:图中所有与△ABC相似的格点三角形中,最大的△A′B′C′如图所示:
S△A′B′C′=×4×2=4,
故答案为4.
三.解答题
21.解:地图与该地区的实际图形相似,相似比就是比例尺为1:20,周长的比就是相似比,设实际周长是xcm,则
24:x=1:20,
解得:x=480,
面积的比等于相似比的平方,设实际面积是ycm2,则
20:y=(1:20)2,
解得y=8000,
答:这个区域的实际周长480cm,面积8000cm2.
22.解:由题意设a=2k,b=3k,c=4k,
∵a+3b﹣2c=15,
∴2k+9k﹣8k=15,
∴k=5,
∴a=10,b=15,c=20,
∴a+b﹣c
=10+15﹣20
=5.
23.解:如图,设AB=1,
∵点E是正方形ABCD的边AB边上的黄金分割点,且AE>EB,
∴AE=GF=,
∴BE=FH=AB﹣AE=,
∴S3:S2=(GF?FH):(BC?BE)
=(×):(1×)
=.
故答案为:.
24.证明:(1)∵DE∥AC,
∴∠DEB=∠FCE,
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC;
(2)∵EF∥AB,
∴==,
∵DE∥AC,
∴==,
∵AD=12,
∴=,
∴BD=6.
25.解:设小芳所在C处到公路南侧PQ的距离为xm,
21.6km/h=21.6×=6m/s,
∵AB∥PQ,
∴△CAB∽△CPQ,
∴,
∴=,
∴x=30,
∴小芳所在C处到公路南侧PQ的距离为30m.
26.解:(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:;
27.解:(1)如图,四边形A1B1C1D1为所作;
(2)如图,四边形A2B2C2D2为所作.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
