2020-2021学年冀教新版九年级上册数学《第26章 解直角三角形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年冀教新版九年级上册数学《第26章 解直角三角形》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 460.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 23:01:45 | ||
图片预览


文档简介
2020-2021学年冀教新版九年级上册数学《第26章
解直角三角形》单元测试卷
一.选择题
1.锐角三角函数tan30°的值是( )
A.1
B.
C.
D.
2.如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB==( )
A.
B.
C.
D.
3.在Rt△ABC中,∠C=90°,sinA=,则sinB的值为( )
A.
B.
C.
D.
4.比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.sinA=
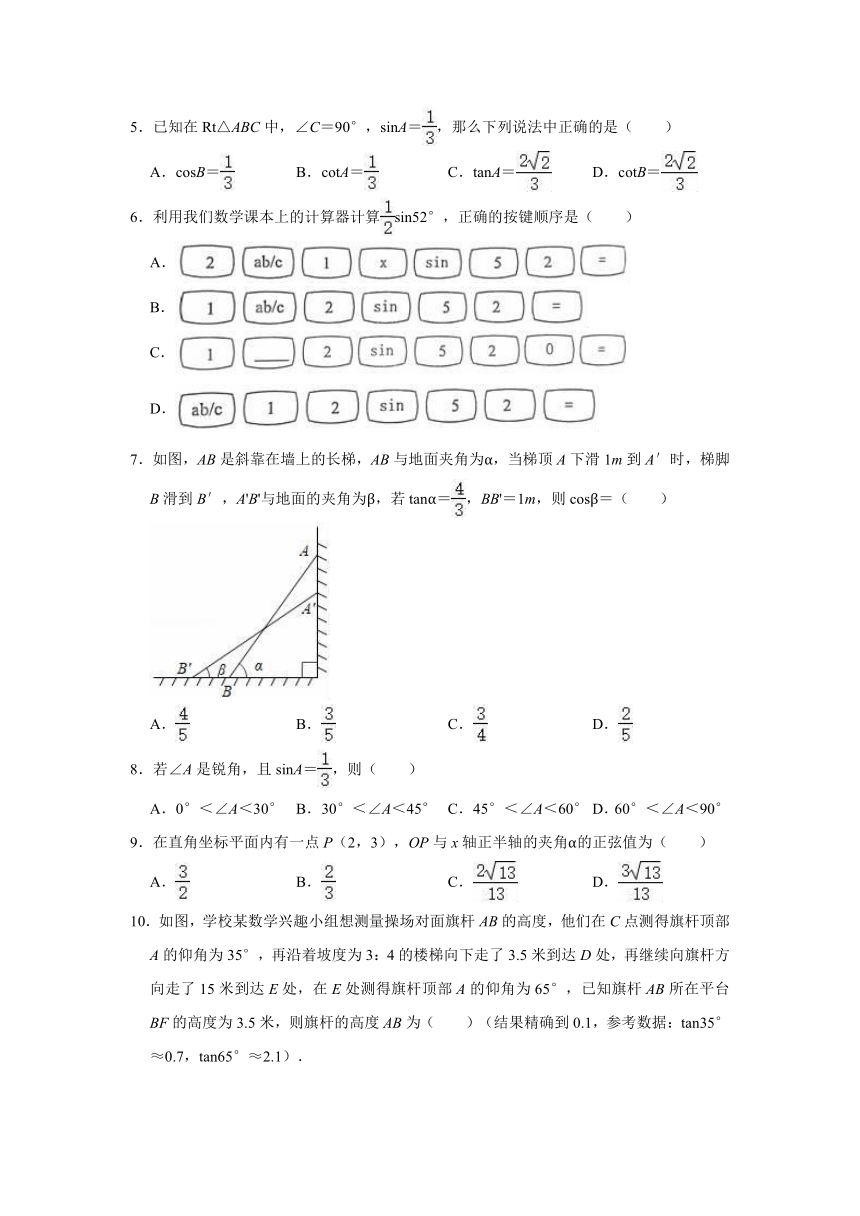
5.已知在Rt△ABC中,∠C=90°,sinA=,那么下列说法中正确的是( )
A.cosB=
B.cotA=
C.tanA=
D.cotB=
6.利用我们数学课本上的计算器计算sin52°,正确的按键顺序是( )
A.
B.
C.
D.
7.如图,AB是斜靠在墙上的长梯,AB与地面夹角为α,当梯顶A下滑1m到A′时,梯脚B滑到B′,A'B'与地面的夹角为β,若tanα=,BB'=1m,则cosβ=( )
A.
B.
C.
D.
8.若∠A是锐角,且sinA=,则( )
A.0°<∠A<30°
B.30°<∠A<45°
C.45°<∠A<60°
D.60°<∠A<90°
9.在直角坐标平面内有一点P(2,3),OP与x轴正半轴的夹角α的正弦值为( )
A.
B.
C.
D.
10.如图,学校某数学兴趣小组想测量操场对面旗杆AB的高度,他们在C点测得旗杆顶部A的仰角为35°,再沿着坡度为3:4的楼梯向下走了3.5米到达D处,再继续向旗杆方向走了15米到达E处,在E处测得旗杆顶部A的仰角为65°,已知旗杆AB所在平台BF的高度为3.5米,则旗杆的高度AB为( )(结果精确到0.1,参考数据:tan35°≈0.7,tan65°≈2.1).
A.19.8米
B.19.7米
C.18.3米
D.16.2米
二.填空题
11.用计算器计算?sin40°=
(精确到0.01).
12.已知α是锐角,且sin(α+15°)=,那么tanα=
.
13.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是
.
14.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为
海里.
15.若sinA=,则tanA=
.
16.在Rt△ABC中,∠C=90°,若tanA=,则cosB的值是
.
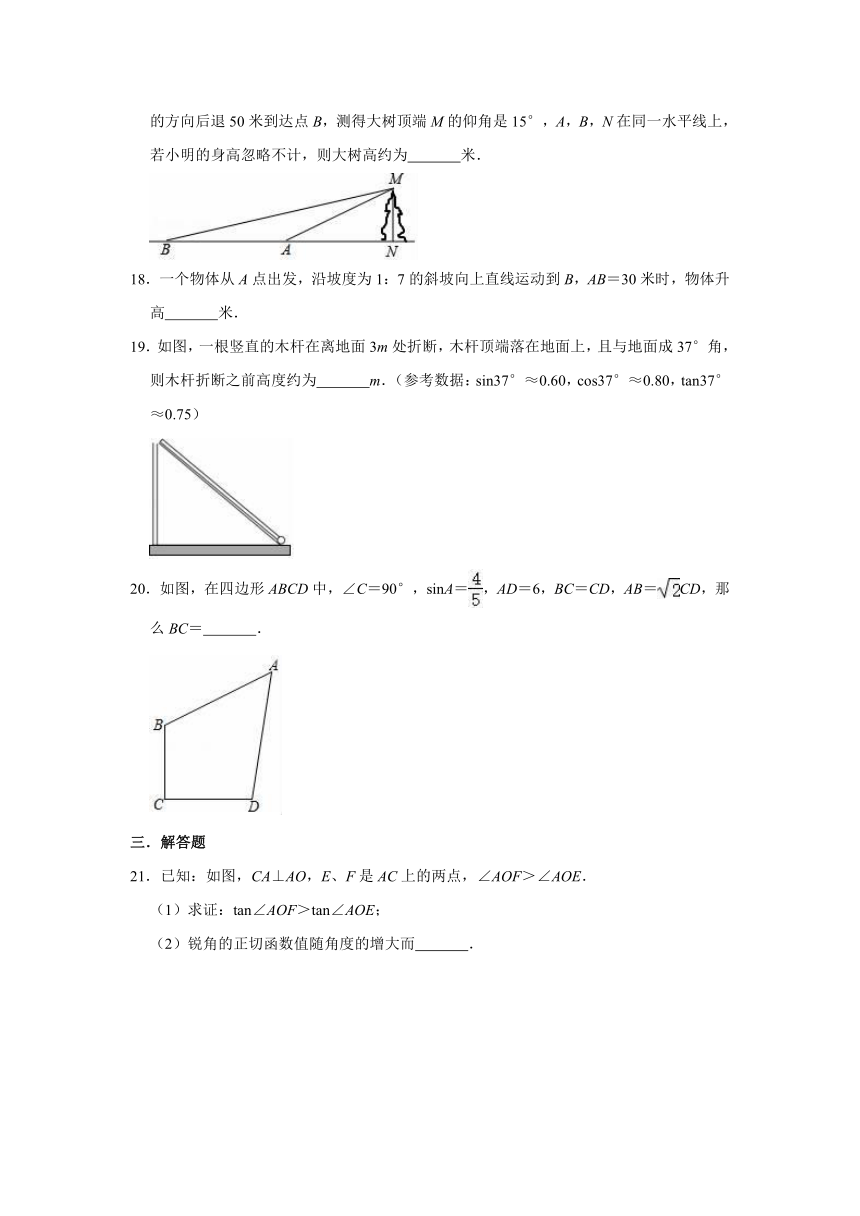
17.如图,小明为测量大树MN的高度,在点A处测得大树顶端M的仰角是30°,沿NA的方向后退50米到达点B,测得大树顶端M的仰角是15°,A,B,N在同一水平线上,若小明的身高忽略不计,则大树高约为
米.
18.一个物体从A点出发,沿坡度为1:7的斜坡向上直线运动到B,AB=30米时,物体升高
米.
19.如图,一根竖直的木杆在离地面3m处折断,木杆顶端落在地面上,且与地面成37°角,则木杆折断之前高度约为
m.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
20.如图,在四边形ABCD中,∠C=90°,sinA=,AD=6,BC=CD,AB=CD,那么BC=
.
三.解答题
21.已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
(1)求证:tan∠AOF>tan∠AOE;
(2)锐角的正切函数值随角度的增大而
.
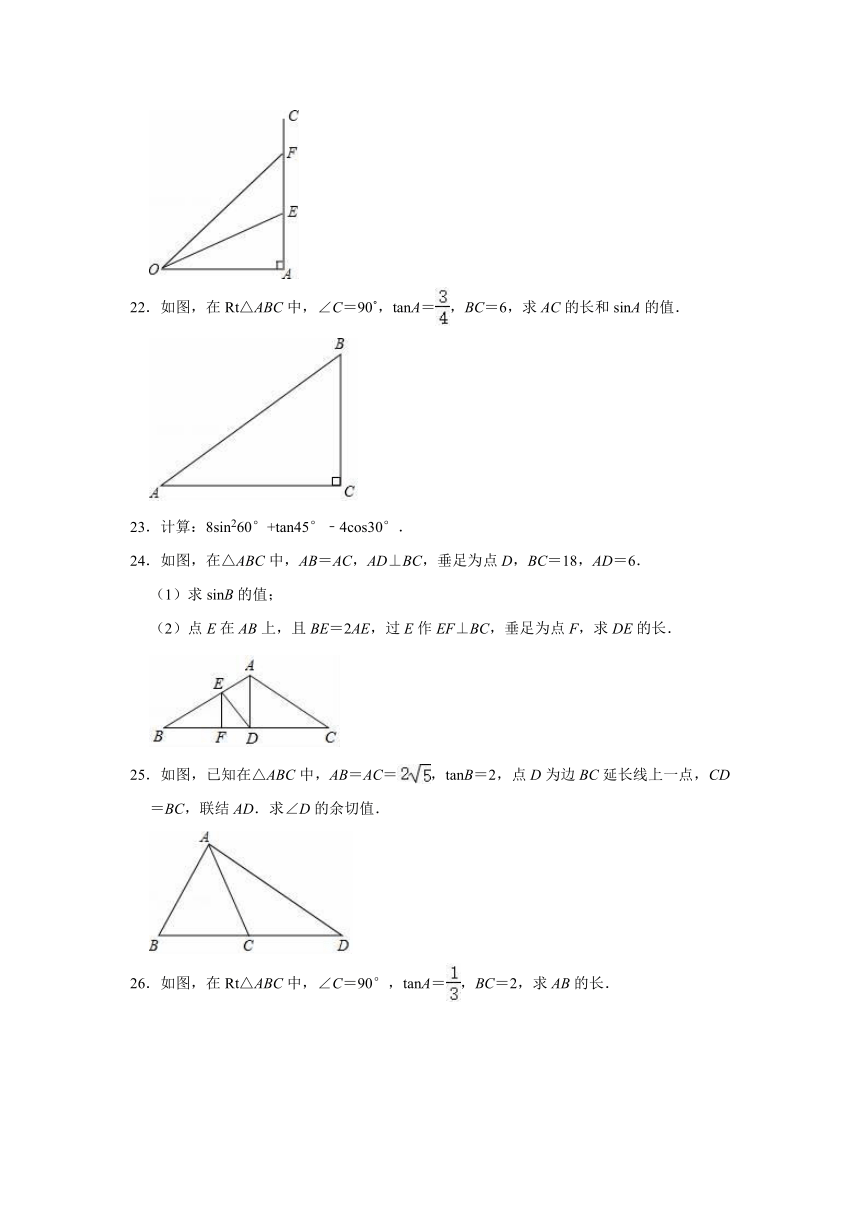
22.如图,在Rt△ABC中,∠C=90?,tanA=,BC=6,求AC的长和sinA的值.
23.计算:8sin260°+tan45°﹣4cos30°.
24.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
25.如图,已知在△ABC中,AB=AC=,tanB=2,点D为边BC延长线上一点,CD=BC,联结AD.求∠D的余切值.
26.如图,在Rt△ABC中,∠C=90°,tanA=,BC=2,求AB的长.
27.如图是某幼儿园的两个同一水平面AF上的长度相同的滑梯模型图,已知滑梯斜面BC=EF=4m,∠ABC=30°,∠EFD=53°,且对角线CE所在的四边形是正方形.若小红从D﹣C﹣B再返回D处,小芳从D﹣C﹣E﹣F再返回D,试计算说明,小红和小芳谁走的路程更短,短多少?(精确到0.1m)(参考数据:sin53°≈,cos53°≈,tan53°≈,)
参考答案与试题解析
一.选择题
1.解:tan30°=.
故选:B.
2.解:∵在Rt△ABC中,∠C=90°,AB=4,AC=3,
∴BC==,
∴cosB==.
故选:C.
3.解:∵Rt△ABC中,∠C=90°,sinA=,
∴cosA===,∠A+∠B=90°,
∴sinB=cosA=.
故选:A.
4.解:在Rt△ABD中,∠ADB=90°,
则sinA=,cosA=,tanA=,
因此选项A正确,选项B、C、D不正确;
故选:A.
5.解:在Rt△ABC中,∠C=90°,sinA=,则cosA===
A、cosB=sinA=,故本选项符合题意.
B、cotA===2.故本选项不符合题意.
C、tanA===.故本选项不符合题意.
D、cotB=tanA=.故本选项不符合题意.
故选:A.
6.解:利用该型号计算器计sin52°,按键顺序正确的是:
,
故选:B.
7.解:如图.∵在直角△ABC中,∠ACB=90°,tanα=,
∴可设AC=4x,那么BC=3x,
∴AB===5x,
∴A′B′=AB=5x.
∵在直角△A′B′C中,∠A′CB′=90°,A′C=4x﹣1,B′C=3x+1,
∴(4x﹣1)2+(3x+1)2=(5x)2,
解得x=1,
∴A′C=3,B′C=4,A′B′=5,
∴cosβ=.
故选:A.
8.解:∵∠A是锐角,且sinA=<=sin30°,
∴0°<∠A<30°,
故选:A.
9.解:如图,作PE⊥x轴于E.
∵P(2,3),
∴OE=2,PE=3,
∴OP===,
∴sinα===,
故选:D.
10.解:作CG⊥AF于G,DH⊥CG于H,如图所示:
则HG=DF,FG=DH,
∵楼梯CD的坡度为3:4,CD=3.5,
∴FG=DH=2.1,CH=2.8,
在Rt△ACG中,∠ACG=35°,tan∠ACG==tan35°≈0.7,
∴AG≈0.7CG,
∴AF=AG+FG=0.7CG+2.1,
∵DF=HG=CG﹣CH=CG﹣2.8,
∴EF=DF﹣DE=CG﹣2.8﹣15=CG﹣17.8,
在Rt△AEF中,∠AEF=65°,tan∠AEF==tan65°≈2.1,
∴AF=2.1EF,
∴0.7CG+2.1=2.1(CG﹣17.8),
解得:CG=28.2,
∴AF=0.7×28.2+2.1=21.84,
∴AB=AF﹣BF=21.84﹣3.5≈18.3(米),
即旗杆的高度AB约为18.3米;
故选:C.
二.填空题
11.解:
sin40°=1.44.(精确到0.01).
故答案为1.44.
12.解:∵sin60°=,
∴α+15°=60°,
解得,α=45°,
∴tanα=tan45°=1,
故答案为:1.
13.解:在Rt△ABC中,cosA==,
故答案为:.
14.解:根据题意得:∠BAC=90°,AB=12海里,AC=9海里,
在Rt△ABC中,BC==15海里,
故答案为:15.
15.解:∵sinA=,
∴∠A=30°,
则tanA=.
故答案为:.
16.解:如图所示:∵∠C=90°,tanA=,
∴=,
设BC=3x,AC=4x,故AB=5x,
则cosB===.
故答案是:.
17.解:∠MAN是△ABM的一个外角,
∴∠AMB=∠MAN﹣∠ABM=30°﹣15°=15°,
∴∠AMB=∠ABM,
∴AM=AB=50米,
在Rt△AMN中,∠MAN=30°,
∴MN=AM=25米;
故答案为:25.
18.解:∵坡度为1:7,
∴设坡角是α,则sinα==,
∴上升的高度是:30×=3(米).
故答案为:3.
19.解:如图:AC=3m,∠B=37°,
∴AB=≈=5,
∴木杆折断之前高度=AC+AB=3+5=8(m).
故答案为8.
20.解:作BE⊥AD于E,连接BD,如图所示:
设BC=CD=x,则AB=x,
∵sinA==,
∴BE=AB=x,
∴AE===x,
∵BC=CD,∠C=90°,
∴BD=BC=x,
∴BD=AB,
∵BE⊥AD,
∴AE=DE=AD=3,
∴x=3,
解得:x=,
即BC=,
故答案为:.
三.解答题
21.解:(1)∵CA⊥AO,
∴△FOA和△EOA均为直角三角形.
∴tan∠AOF=,tan∠AOE=.
∴tan∠AOF>tan∠AOE.
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
故答案为:增大.
22.解:∵△ABC中,tanA=,BC=6,
∴=,
∴AC=8,
∴AB===10,
∴sinA==
23.解:原式=8×()2+1﹣4×
=8×+1﹣2
=6+1﹣2
=7﹣2.
24.解:(1)∵AB=AC,AD⊥BC,BC=18,
∴BD=DC=BC=9,
∴AB===3,
∴sinB===;
(2)∵AD⊥BC,EF⊥BC,
∴EF∥AD,
∴===,
∴EF=AD=×6=4,BF=BD=×9=6,
∴DF=BD﹣BF=9﹣6=3,
在Rt△DEF中,DE===5.
25.解:过点A作AH⊥BH
∵
∴在Rt△ABH中
AB2=AH2+BH2
解得BH=2,
则AH=4,
∵AB=AC,AH⊥BC
∴HC=BH=2
∴CD=BC=2BH=4
∴HD=HC+CD=6
26.解:∵在Rt△ABC中,∠C=90°,
∴tanA==.
∵BC=2,
∴=,AC=6.
∵AB2=AC2+BC2=40,
∴AB=.
27.解:小红走的路程更短,约短0.63m,理由如下:
如图所示:
由题意得:DG=AC,∠EDF=∠BAC=90°,∠ABC=30°,
∴DG=AC=BC=2m,AB=AC=2m,
∵sin∠EFD=,cos∠EFD=,
∴DE=EF×sin53°≈4×=3.2(m),DF=EF×cos35°≈4×=2.4(m),
∴EG=DE﹣DG=1.2m,
∵四边形CGEH是正方形,
∴CE=EG=×1.2≈1.69(m),
∵小红从D﹣C﹣B再返回D处,小芳从D﹣C﹣E﹣F再返回D,
∴小红走的路程为CD+BC+BA+AD,小芳走的路程为CD+CE+EF+DF,
∴小芳比小红走的路程短AB+AD﹣CE﹣DF=2+1.2﹣1.69﹣2.4≈0.6(m).
解直角三角形》单元测试卷
一.选择题
1.锐角三角函数tan30°的值是( )
A.1
B.
C.
D.
2.如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB==( )
A.
B.
C.
D.
3.在Rt△ABC中,∠C=90°,sinA=,则sinB的值为( )
A.
B.
C.
D.
4.比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.sinA=
5.已知在Rt△ABC中,∠C=90°,sinA=,那么下列说法中正确的是( )
A.cosB=
B.cotA=
C.tanA=
D.cotB=
6.利用我们数学课本上的计算器计算sin52°,正确的按键顺序是( )
A.
B.
C.
D.
7.如图,AB是斜靠在墙上的长梯,AB与地面夹角为α,当梯顶A下滑1m到A′时,梯脚B滑到B′,A'B'与地面的夹角为β,若tanα=,BB'=1m,则cosβ=( )
A.
B.
C.
D.
8.若∠A是锐角,且sinA=,则( )
A.0°<∠A<30°
B.30°<∠A<45°
C.45°<∠A<60°
D.60°<∠A<90°
9.在直角坐标平面内有一点P(2,3),OP与x轴正半轴的夹角α的正弦值为( )
A.
B.
C.
D.
10.如图,学校某数学兴趣小组想测量操场对面旗杆AB的高度,他们在C点测得旗杆顶部A的仰角为35°,再沿着坡度为3:4的楼梯向下走了3.5米到达D处,再继续向旗杆方向走了15米到达E处,在E处测得旗杆顶部A的仰角为65°,已知旗杆AB所在平台BF的高度为3.5米,则旗杆的高度AB为( )(结果精确到0.1,参考数据:tan35°≈0.7,tan65°≈2.1).
A.19.8米
B.19.7米
C.18.3米
D.16.2米
二.填空题
11.用计算器计算?sin40°=
(精确到0.01).
12.已知α是锐角,且sin(α+15°)=,那么tanα=
.
13.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是
.
14.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为
海里.
15.若sinA=,则tanA=
.
16.在Rt△ABC中,∠C=90°,若tanA=,则cosB的值是
.
17.如图,小明为测量大树MN的高度,在点A处测得大树顶端M的仰角是30°,沿NA的方向后退50米到达点B,测得大树顶端M的仰角是15°,A,B,N在同一水平线上,若小明的身高忽略不计,则大树高约为
米.
18.一个物体从A点出发,沿坡度为1:7的斜坡向上直线运动到B,AB=30米时,物体升高
米.
19.如图,一根竖直的木杆在离地面3m处折断,木杆顶端落在地面上,且与地面成37°角,则木杆折断之前高度约为
m.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
20.如图,在四边形ABCD中,∠C=90°,sinA=,AD=6,BC=CD,AB=CD,那么BC=
.
三.解答题
21.已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
(1)求证:tan∠AOF>tan∠AOE;
(2)锐角的正切函数值随角度的增大而
.
22.如图,在Rt△ABC中,∠C=90?,tanA=,BC=6,求AC的长和sinA的值.
23.计算:8sin260°+tan45°﹣4cos30°.
24.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
25.如图,已知在△ABC中,AB=AC=,tanB=2,点D为边BC延长线上一点,CD=BC,联结AD.求∠D的余切值.
26.如图,在Rt△ABC中,∠C=90°,tanA=,BC=2,求AB的长.
27.如图是某幼儿园的两个同一水平面AF上的长度相同的滑梯模型图,已知滑梯斜面BC=EF=4m,∠ABC=30°,∠EFD=53°,且对角线CE所在的四边形是正方形.若小红从D﹣C﹣B再返回D处,小芳从D﹣C﹣E﹣F再返回D,试计算说明,小红和小芳谁走的路程更短,短多少?(精确到0.1m)(参考数据:sin53°≈,cos53°≈,tan53°≈,)
参考答案与试题解析
一.选择题
1.解:tan30°=.
故选:B.
2.解:∵在Rt△ABC中,∠C=90°,AB=4,AC=3,
∴BC==,
∴cosB==.
故选:C.
3.解:∵Rt△ABC中,∠C=90°,sinA=,
∴cosA===,∠A+∠B=90°,
∴sinB=cosA=.
故选:A.
4.解:在Rt△ABD中,∠ADB=90°,
则sinA=,cosA=,tanA=,
因此选项A正确,选项B、C、D不正确;
故选:A.
5.解:在Rt△ABC中,∠C=90°,sinA=,则cosA===
A、cosB=sinA=,故本选项符合题意.
B、cotA===2.故本选项不符合题意.
C、tanA===.故本选项不符合题意.
D、cotB=tanA=.故本选项不符合题意.
故选:A.
6.解:利用该型号计算器计sin52°,按键顺序正确的是:
,
故选:B.
7.解:如图.∵在直角△ABC中,∠ACB=90°,tanα=,
∴可设AC=4x,那么BC=3x,
∴AB===5x,
∴A′B′=AB=5x.
∵在直角△A′B′C中,∠A′CB′=90°,A′C=4x﹣1,B′C=3x+1,
∴(4x﹣1)2+(3x+1)2=(5x)2,
解得x=1,
∴A′C=3,B′C=4,A′B′=5,
∴cosβ=.
故选:A.
8.解:∵∠A是锐角,且sinA=<=sin30°,
∴0°<∠A<30°,
故选:A.
9.解:如图,作PE⊥x轴于E.
∵P(2,3),
∴OE=2,PE=3,
∴OP===,
∴sinα===,
故选:D.
10.解:作CG⊥AF于G,DH⊥CG于H,如图所示:
则HG=DF,FG=DH,
∵楼梯CD的坡度为3:4,CD=3.5,
∴FG=DH=2.1,CH=2.8,
在Rt△ACG中,∠ACG=35°,tan∠ACG==tan35°≈0.7,
∴AG≈0.7CG,
∴AF=AG+FG=0.7CG+2.1,
∵DF=HG=CG﹣CH=CG﹣2.8,
∴EF=DF﹣DE=CG﹣2.8﹣15=CG﹣17.8,
在Rt△AEF中,∠AEF=65°,tan∠AEF==tan65°≈2.1,
∴AF=2.1EF,
∴0.7CG+2.1=2.1(CG﹣17.8),
解得:CG=28.2,
∴AF=0.7×28.2+2.1=21.84,
∴AB=AF﹣BF=21.84﹣3.5≈18.3(米),
即旗杆的高度AB约为18.3米;
故选:C.
二.填空题
11.解:
sin40°=1.44.(精确到0.01).
故答案为1.44.
12.解:∵sin60°=,
∴α+15°=60°,
解得,α=45°,
∴tanα=tan45°=1,
故答案为:1.
13.解:在Rt△ABC中,cosA==,
故答案为:.
14.解:根据题意得:∠BAC=90°,AB=12海里,AC=9海里,
在Rt△ABC中,BC==15海里,
故答案为:15.
15.解:∵sinA=,
∴∠A=30°,
则tanA=.
故答案为:.
16.解:如图所示:∵∠C=90°,tanA=,
∴=,
设BC=3x,AC=4x,故AB=5x,
则cosB===.
故答案是:.
17.解:∠MAN是△ABM的一个外角,
∴∠AMB=∠MAN﹣∠ABM=30°﹣15°=15°,
∴∠AMB=∠ABM,
∴AM=AB=50米,
在Rt△AMN中,∠MAN=30°,
∴MN=AM=25米;
故答案为:25.
18.解:∵坡度为1:7,
∴设坡角是α,则sinα==,
∴上升的高度是:30×=3(米).
故答案为:3.
19.解:如图:AC=3m,∠B=37°,
∴AB=≈=5,
∴木杆折断之前高度=AC+AB=3+5=8(m).
故答案为8.
20.解:作BE⊥AD于E,连接BD,如图所示:
设BC=CD=x,则AB=x,
∵sinA==,
∴BE=AB=x,
∴AE===x,
∵BC=CD,∠C=90°,
∴BD=BC=x,
∴BD=AB,
∵BE⊥AD,
∴AE=DE=AD=3,
∴x=3,
解得:x=,
即BC=,
故答案为:.
三.解答题
21.解:(1)∵CA⊥AO,
∴△FOA和△EOA均为直角三角形.
∴tan∠AOF=,tan∠AOE=.
∴tan∠AOF>tan∠AOE.
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
故答案为:增大.
22.解:∵△ABC中,tanA=,BC=6,
∴=,
∴AC=8,
∴AB===10,
∴sinA==
23.解:原式=8×()2+1﹣4×
=8×+1﹣2
=6+1﹣2
=7﹣2.
24.解:(1)∵AB=AC,AD⊥BC,BC=18,
∴BD=DC=BC=9,
∴AB===3,
∴sinB===;
(2)∵AD⊥BC,EF⊥BC,
∴EF∥AD,
∴===,
∴EF=AD=×6=4,BF=BD=×9=6,
∴DF=BD﹣BF=9﹣6=3,
在Rt△DEF中,DE===5.
25.解:过点A作AH⊥BH
∵
∴在Rt△ABH中
AB2=AH2+BH2
解得BH=2,
则AH=4,
∵AB=AC,AH⊥BC
∴HC=BH=2
∴CD=BC=2BH=4
∴HD=HC+CD=6
26.解:∵在Rt△ABC中,∠C=90°,
∴tanA==.
∵BC=2,
∴=,AC=6.
∵AB2=AC2+BC2=40,
∴AB=.
27.解:小红走的路程更短,约短0.63m,理由如下:
如图所示:
由题意得:DG=AC,∠EDF=∠BAC=90°,∠ABC=30°,
∴DG=AC=BC=2m,AB=AC=2m,
∵sin∠EFD=,cos∠EFD=,
∴DE=EF×sin53°≈4×=3.2(m),DF=EF×cos35°≈4×=2.4(m),
∴EG=DE﹣DG=1.2m,
∵四边形CGEH是正方形,
∴CE=EG=×1.2≈1.69(m),
∵小红从D﹣C﹣B再返回D处,小芳从D﹣C﹣E﹣F再返回D,
∴小红走的路程为CD+BC+BA+AD,小芳走的路程为CD+CE+EF+DF,
∴小芳比小红走的路程短AB+AD﹣CE﹣DF=2+1.2﹣1.69﹣2.4≈0.6(m).
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
