人教版八年级数学上册 12.3.2 角平分线的判定 课件(15张)
文档属性
| 名称 | 人教版八年级数学上册 12.3.2 角平分线的判定 课件(15张) |
|
|
| 格式 | zip | ||
| 文件大小 | 370.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
点在角平分线上
点到角两边的距离相等
性质
是否成立?
12.3
角平分线的判定
学习目标(1分钟)
1.掌握角平分线判定定理; 2.会用角平分线判定定理解决问题.
自学指导(5分钟)
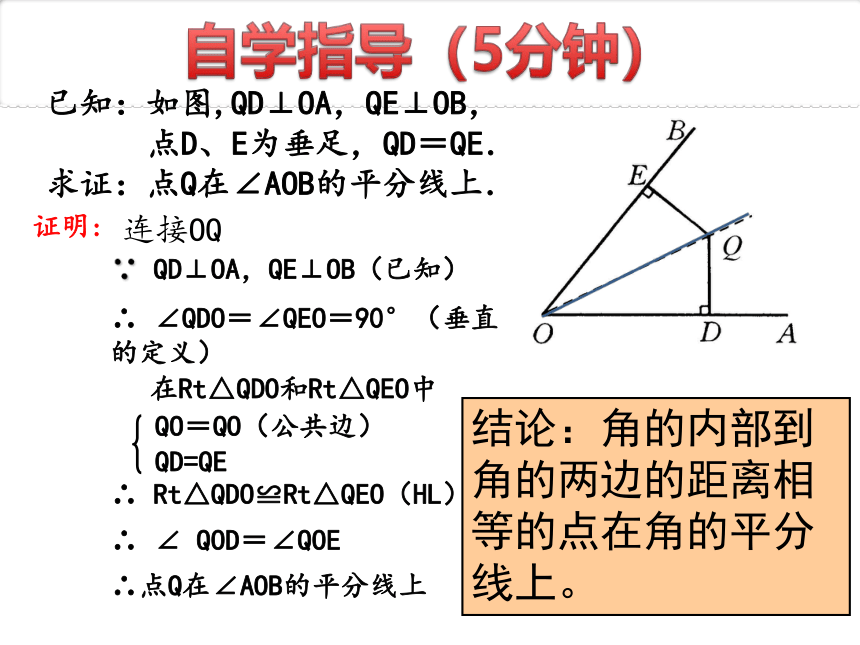
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
∵
QD⊥OA,QE⊥OB(已知)
∴
∠QDO=∠QEO=90°(垂直的定义)
在Rt△QDO和Rt△QEO中
QO=QO(公共边)
QD=QE
∴
Rt△QDO≌Rt△QEO(HL)
∴
∠
QOD=∠QOE
∴点Q在∠AOB的平分线上
连接OQ
结论:角的内部到角的两边的距离相等的点在角的平分线上。
自学指导(5分钟)
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
∵
QD⊥OA,QE⊥OB(已知)
∴
∠QDO=∠QEO=90°(垂直的定义)
在Rt△QDO和Rt△QEO中
QO=QO(公共边)
QD=QE
∴
Rt△QDO≌Rt△QEO(HL)
∴
∠
QOD=∠QOE
∴点Q在∠AOB的平分线上
连接OQ
结论:角的内部到角的两边的距离相等的点在角的平分线上。
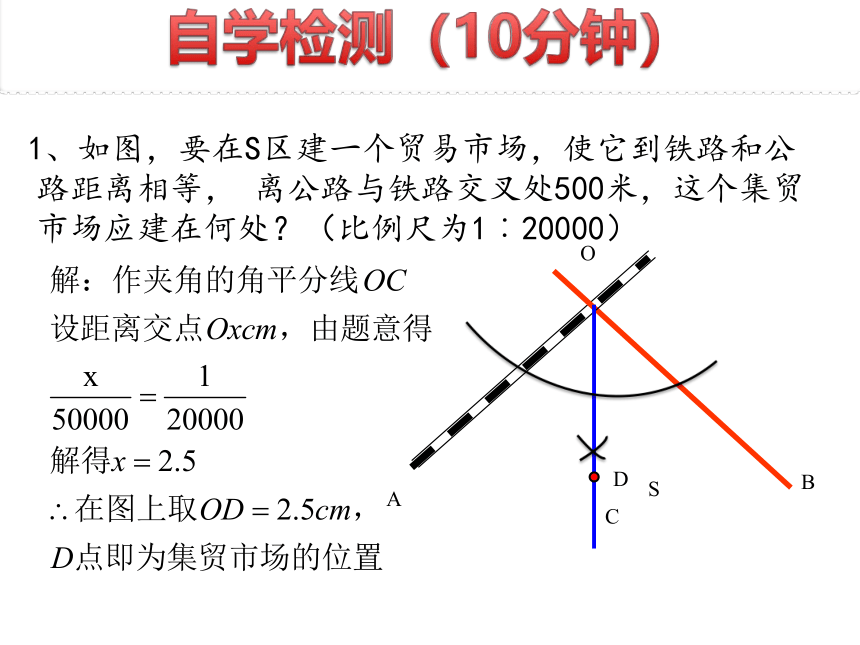
1、如图,要在S区建一个贸易市场,使它到铁路和公路距离相等,
离公路与铁路交叉处500米,这个集贸市场应建在何处?(比例尺为1︰20000)
D
C
S
自学检测(10分钟)
O
A
B
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
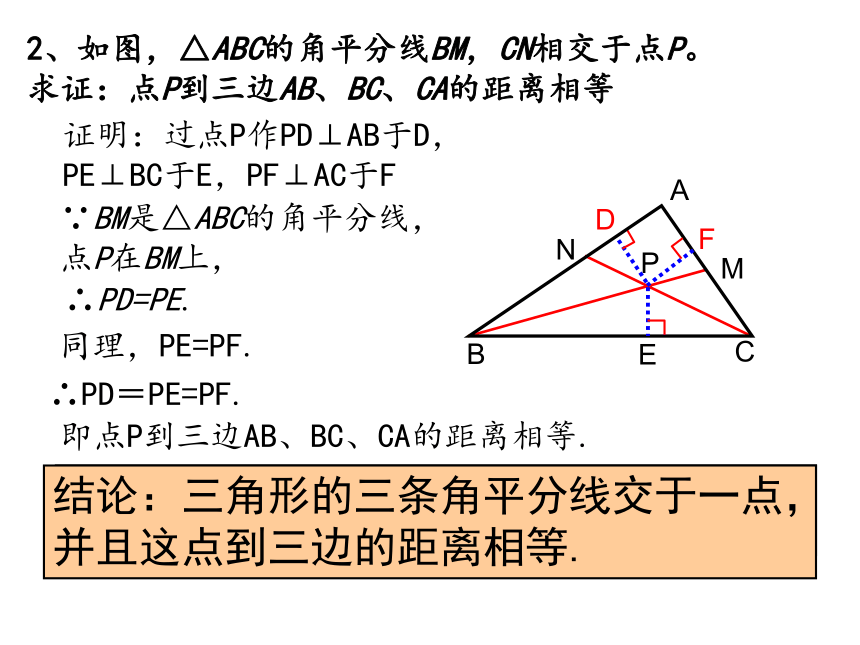
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F
2、如图,△ABC的角平分线BM,CN相交于点P。
求证:点P到三边AB、BC、CA的距离相等
D
P
M
N
A
B
C
F
E
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
3、如图所示是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
4、如图,∠AOB=70°,QC⊥OA于C,
QD⊥OB于D,若QC=QD,则∠AOQ=____°
C
35
点拨运用(3分钟)
1.角的内部到角的两边的距离相等的点在角的平分线上
用符号语言表示为:
∵
PD⊥OA,PE⊥OB,
PD=PE.
∴点P在∠AOB的平分线上。
P
A
O
B
C
E
D
2.有关到线段距离相等的点的位置确定方法
(1)当点指定在三角形内部时,只要作出内角的平分线的交点即可;
(2)在点没有指定在三角形内部时,要注意画出内角平分线的交点和外角平分线的交点,这时交点有多个.
课堂小结(1分钟)
1、画任意角的角的平分线;
2、角的平分线的性质。
点在角平分线上
点到角两边的距离相等
性质
判定
(证明两条线段相等的依据)
(证明两角相等的依据)
当堂训练(15分钟)
1、在以下结论中,不正确的是(????)?
A.平面内到角的两边的距离相等的点一定在角平
分线上?
B.角平分线上任一点到角的两边的距离一定相等?
C.一个角只有一条角平分线?
D.角的平分线有时是直线,有时是线段
2、在△ABC中,∠B=∠ACB,CD是∠ACB的角平分线,
已知∠ADC=105°,则∠A的度数为(????)
A.40°???B.36°????C.70°????D.60°
3、已知Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,
若BC=32,且BD:CD=9:7,则D到AB边的距离为(????)?
A.18???B.16????C.14????????D.?12?
D
A
C
当堂训练(15分钟)
4、如图,已知PA⊥ON于点A,PB⊥OM于
点B,且PA=PB,∠MON=50°,∠OPC=30°,
则∠PCA的度数是______.
5、某地为了发展旅游业,要在三条
公路上修建一个度假村,使度假村到
三条公路的距离相等,这个度假
村的选址地点共有( )
A.1处
B.2处
C.3处
D.4处
55°
D
选做题
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的
等量关系并给予证明.
(1)证明:∵DE⊥AB于E
DF⊥AC于F
∴∠E=∠AFD=∠DFC=90
°
在Rt△BDE和Rt△CDF中,
∵BD=CD,BE=CF
∴
Rt△BDE
≌
Rt△CDF(HL)
∴DE=DF
∴
AD平分∠BAC
选做题
(2)猜想:AB+AC=2AE
证明:由(1)得AD平分∠BAC
∴∠EAD=∠DAF
DE=DF
在Rt△ADE和Rt△ADF中
∠EAD=∠DAF
∠E=∠AFD=90
°
DE=DF
∴Rt△ADE
≌
Rt△ADF(AAS)
∴AE=AF
∵BE=CF
∴
AB+AC=AB+AF+FC=AB+AE+BE=AE+AE=2AE
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的
等量关系并给予证明.
板书设计
定理:角的内部到角的两边的距离相等的点在角的平分线上。
P
A
O
B
C
E
D
点在角平分线上
点到角两边的距离相等
性质
是否成立?
12.3
角平分线的判定
学习目标(1分钟)
1.掌握角平分线判定定理; 2.会用角平分线判定定理解决问题.
自学指导(5分钟)
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
∵
QD⊥OA,QE⊥OB(已知)
∴
∠QDO=∠QEO=90°(垂直的定义)
在Rt△QDO和Rt△QEO中
QO=QO(公共边)
QD=QE
∴
Rt△QDO≌Rt△QEO(HL)
∴
∠
QOD=∠QOE
∴点Q在∠AOB的平分线上
连接OQ
结论:角的内部到角的两边的距离相等的点在角的平分线上。
自学指导(5分钟)
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
∵
QD⊥OA,QE⊥OB(已知)
∴
∠QDO=∠QEO=90°(垂直的定义)
在Rt△QDO和Rt△QEO中
QO=QO(公共边)
QD=QE
∴
Rt△QDO≌Rt△QEO(HL)
∴
∠
QOD=∠QOE
∴点Q在∠AOB的平分线上
连接OQ
结论:角的内部到角的两边的距离相等的点在角的平分线上。
1、如图,要在S区建一个贸易市场,使它到铁路和公路距离相等,
离公路与铁路交叉处500米,这个集贸市场应建在何处?(比例尺为1︰20000)
D
C
S
自学检测(10分钟)
O
A
B
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F
2、如图,△ABC的角平分线BM,CN相交于点P。
求证:点P到三边AB、BC、CA的距离相等
D
P
M
N
A
B
C
F
E
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
3、如图所示是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
4、如图,∠AOB=70°,QC⊥OA于C,
QD⊥OB于D,若QC=QD,则∠AOQ=____°
C
35
点拨运用(3分钟)
1.角的内部到角的两边的距离相等的点在角的平分线上
用符号语言表示为:
∵
PD⊥OA,PE⊥OB,
PD=PE.
∴点P在∠AOB的平分线上。
P
A
O
B
C
E
D
2.有关到线段距离相等的点的位置确定方法
(1)当点指定在三角形内部时,只要作出内角的平分线的交点即可;
(2)在点没有指定在三角形内部时,要注意画出内角平分线的交点和外角平分线的交点,这时交点有多个.
课堂小结(1分钟)
1、画任意角的角的平分线;
2、角的平分线的性质。
点在角平分线上
点到角两边的距离相等
性质
判定
(证明两条线段相等的依据)
(证明两角相等的依据)
当堂训练(15分钟)
1、在以下结论中,不正确的是(????)?
A.平面内到角的两边的距离相等的点一定在角平
分线上?
B.角平分线上任一点到角的两边的距离一定相等?
C.一个角只有一条角平分线?
D.角的平分线有时是直线,有时是线段
2、在△ABC中,∠B=∠ACB,CD是∠ACB的角平分线,
已知∠ADC=105°,则∠A的度数为(????)
A.40°???B.36°????C.70°????D.60°
3、已知Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,
若BC=32,且BD:CD=9:7,则D到AB边的距离为(????)?
A.18???B.16????C.14????????D.?12?
D
A
C
当堂训练(15分钟)
4、如图,已知PA⊥ON于点A,PB⊥OM于
点B,且PA=PB,∠MON=50°,∠OPC=30°,
则∠PCA的度数是______.
5、某地为了发展旅游业,要在三条
公路上修建一个度假村,使度假村到
三条公路的距离相等,这个度假
村的选址地点共有( )
A.1处
B.2处
C.3处
D.4处
55°
D
选做题
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的
等量关系并给予证明.
(1)证明:∵DE⊥AB于E
DF⊥AC于F
∴∠E=∠AFD=∠DFC=90
°
在Rt△BDE和Rt△CDF中,
∵BD=CD,BE=CF
∴
Rt△BDE
≌
Rt△CDF(HL)
∴DE=DF
∴
AD平分∠BAC
选做题
(2)猜想:AB+AC=2AE
证明:由(1)得AD平分∠BAC
∴∠EAD=∠DAF
DE=DF
在Rt△ADE和Rt△ADF中
∠EAD=∠DAF
∠E=∠AFD=90
°
DE=DF
∴Rt△ADE
≌
Rt△ADF(AAS)
∴AE=AF
∵BE=CF
∴
AB+AC=AB+AF+FC=AB+AE+BE=AE+AE=2AE
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的
等量关系并给予证明.
板书设计
定理:角的内部到角的两边的距离相等的点在角的平分线上。
P
A
O
B
C
E
D
