人教版七年级数学上册 2.1.1用字母表示数的教案
文档属性
| 名称 | 人教版七年级数学上册 2.1.1用字母表示数的教案 |  | |
| 格式 | zip | ||
| 文件大小 | 85.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 08:55:54 | ||
图片预览



文档简介
2.1.1
用字母表示数
教学目标:
通过实例,进一步体验用字母表示数的意义。
理解字母与数一起参与运算的意义。
会利用字母表示数表示简单的数量关系和数学规律。
掌握字母与数一起参与运算时的正确写法。
教学重点:
用字母表示数的意义。
教学难点:
用字母表示数学规律,会用含有字母的式子表示实际问题中的数量关系。
教学过程:
问题引入:
K先生正在看《阿Q正传》,这里K、Q表示什么?字母可表示:人名。
从A地到B地要走3个小时.这里A、B表示什么?字母可表示:地名。
加法交换律:a+b=b+a。字母可表示:运算定律。
设计意图:
情景导入
2016年9月15日,中国在酒泉卫星发射中心用长征二号FT2火箭将天宫二号空间实验室发射升空.它在椭圆形轨道上环绕地球飞过1周,约需90分钟.请问:
(1)绕地球飞行10周约需多少分钟?
(2)绕地球飞行n周约需多少分钟?
设计意图:
知识点一:含字母的式子的书写
例1
用含有字母的式子表示下列数量
练习簿的单价为a元,100本练习簿的总价是100a元。
练习簿的单价为b
元,
a本练习簿的总价是ab元。
练习簿的单价为0.5元,圆珠笔的单价是3.2元,买a本练习簿和b支笔的总价是(0.5a+3.2b)元。
小明的家离学校s千米,小明骑车上学.若每小时行10千米,则需时。
若每斤苹果元,则买m斤苹果需元。
姚明个字高,经测量他通常跨一步的距离1米,若取向前为正,向后为负,那么姚明向前跨a步为a米,向后跨a步为-a米。
例题
判断下列式子书写是否规范,不规范的请改正。
,
,,,
答案:,,,,
知识点二
用含字母的式子表示数量关系
例题
一条河的水流速度是2.5
km/h,船在静水中的速度是
v
km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度?
答案:顺水速度=静水速度+水流速度=(v+2.5)km/h
逆水速度=静水速度-水流速度=(v-2.5)km/h
例题
买一个篮球需要x元,买一个排球需要y元,买一个足球需要
z
元,用式子表示买
3个篮球、5个排球、2个足球共需要的钱数;
解:买3个篮球、5个排球、2个足球共需要(3x+5y+2z)
元
例题
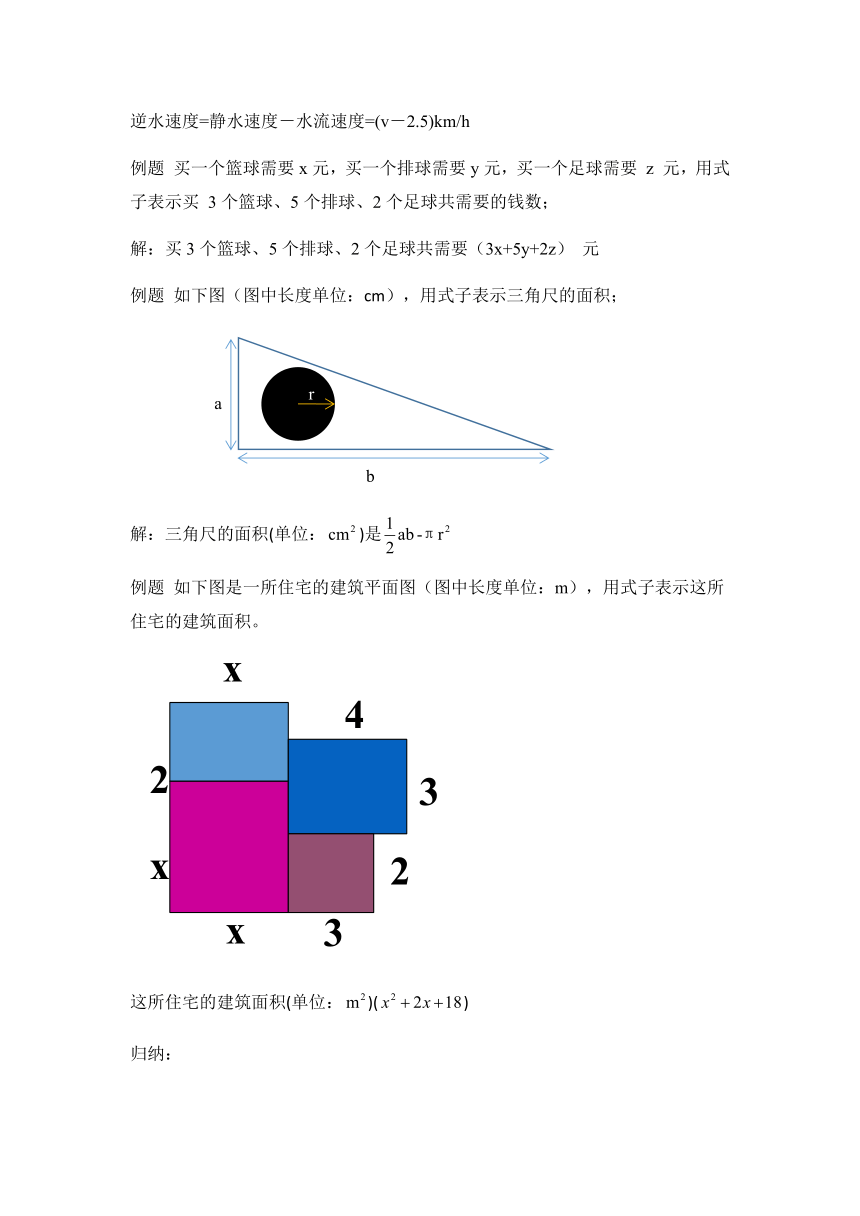
如下图(图中长度单位:cm),用式子表示三角尺的面积;
解:三角尺的面积(单位:)是
例题
如下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积。
这所住宅的建筑面积(单位:)()
归纳:
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言。
要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
理清语句层次明确运算顺序;
牢记一些概念和公式。
练一练
某种商品每袋4.8元,在一个月内的销售量是m
袋,用式子表示在这个月内销售这种商品的收入。
4.8m元
圆柱体的底面半径、高分别是
r,h,用式子表示圆柱体的体积。
有两片棉田,一片有m
(公顷,1
=104
),平均每公顷产棉花a
kg;另一片有n
,平均每公顷产棉花b
kg,用式子表示两片棉田上棉花的总产量。
(am+bn)kg
知识点三
用字母表示规律
如图所示,搭一个正方形需要4根火柴棒。
按上面的方式,搭2个正方形需要7根火柴,搭3个正方形需要10根火柴。搭7个这样的正方形需要22根火柴。
如果用
x
表示所搭正方形的个数,
那么搭
x
个这样的正方形需要多少根火柴?
答:4+3×(x-1)或1+3×x
做一做
根据你的计算方法,搭200个这样的正方形需要601根火柴棒;
搭2017个这样的正方形需要6052根火柴棒。
当堂练习
(1)5箱苹果重m
kg,每箱重kg
;
(2)一个数比a的2倍小5,则这个数为(2a-5);
(3)全校学生总数是x,其中女生占总数52%,则女生人数是0.52x,男生人数是0.48x;
(4)某班有a名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共(4a-25)本。
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号。
科学家爱因斯坦在谈成功的秘诀时,写下了一个公式:A=X+Y+Z,他解释道:A代表成功,X代表艰苦的劳动,
Y代表正确的方法,Z代表少说空话。
讲授新课:
(一)
例题教学
字母还可以表示哪些数呢?学生小组
讨论交流,然后由代表发言。学生会结合自己的生活经验得出字母可以
表示任何数。
师同时说明
利用字母表示
数,能把数和数量关系一般化、简明的表示出来,并
顺势投影显示例题:
例
1
(
1
)练习簿的单价为
a
元,
100
本练习簿的总价是
元。
(
2
)练习簿的单价为
a
元,
b
本练习簿的总价是
元。
(
3
)练习簿的单价为
0.5
元
,
圆珠笔的单价是
3.2
元,买
a
本练习簿和
b
支笔的总价是
元。
(
4
)
练习簿的单价为a元
,
如果买练习簿总共花去了c元,
则买了
本练习簿?
根据总价
=
单价×数量,学生很容易得出。
师在学生回答的基础上进行适当的引导与指点,并指出利用字母表示数时的书写要点。
(二)
练一练:
1
、填空
:⑴、
父亲的年龄比儿子大
28
岁。如果用
x
表示儿子现在的年龄,那么父亲现在的年龄为
岁。(师:后接单位的相加式子要用括号括起来)
⑵、设奶粉每听
p元,橘子每听q元,则买
10
听奶粉、
6
听橘子共需
元。
⑶、长方形的长是
a米,宽是
3
米
,则面积是
平方米,周长是
米。
⑷、小明每时走v千米,
1
时走
千米,
36
分走
千米,
t时走
千米。
(师提醒:带分数与字母相乘是要写成假分数)
⑸、a(a≠
0
)的倒数是
,a的相反数是
。
⑺、面积为
s
的正方形的边长为
。
指学生回答,并要求学生说说你是怎样表示出来的。并
一起总结,然后给出书写时应该注意的事项:
(
1
)
数和表示数的字母相乘,或字母和字母相乘时,乘号可以省略不写,或用“
.
”来代替
;(
2
)
数和字母相乘,在省略乘号时,要把数字写在字母的前面。如
100
×a
可以简写为
100
a
;(
3
)
带分数化为假分数写在字母前;
如
应写成
;
(
4
)后接单位的相加或相减的式子必须用括号;
(5)
除法运算写成分数形式,除号改为分数线
;(
6
)
特别注意:
1
乘以字母时,
1
可以省略不写,如
1
×
a
可写成
a;
-1
乘以字母时,只要在那个字母前加上“
-
”号,
-1
×
a
可写成
-a;
2
、下列表述中,字母各表示什么?
(
1
)圆的面积为
,圆的周长为
2
。
(提醒学生
是圆周率,不是字母
)
(
2
)买
10
件衬衣需
10
s
元。
(
3
)底面积为
50
的长方体的体积为
100
。
(
4
)一条高为
4
的三角形的面积为
2
。
(
5
)教师抽查了班里
学生的作业,共有
本。
(三)合作学习
1
、
师:我们在小学时已经学过一些运算律,你能说出一些运算律吗?(一学生口述运算律,同桌口述用语言文字描述相应的运算律)。
生
1
:加法交换律:交换两个加数的位置,和不变;
生
2
:乘法结合律:三个数相乘,先把前两个数相乘,再乘以第三个数;或者先把后两个数相乘,再乘以第一个数,所得的积不变。
……
师:用语言文字描述运算律比较麻烦,今天我们学习了用字母来表示
数能简明地表示一些数学规律,用字母表示数学规律时,首先要对数学规律的内容充分了解,要表示的数学规律涉及的数量关系是相等关系,还是不等关系;涉及哪些运算;涉及哪些数学符号等。
在师的指导下让学生体会用字母表示学生已学过的运算律并适当的指定并予以表扬、鼓励学生。
2
、
你能用字母表示数来表示下列数学规律吗?
(
1
)互为相反数的两数之和等于
0
。
(
2
)任何一个负数的绝对值大于它本身。
(
3
)一个负数的绝对值等于它的相反数。
(
4
)任何一个不为
0
的数与它的倒数的积等于
1
。
师:互为相反数的两数之和等于
0
,
这
条
数学规律描述的数量关系是相等关系
,
涉及的数学符号
有相反数,涉及的运算有加法,因此
用字母来表示数的方法表示这个数学规律为
(学生自行完成
2
、
3
、
4
小题)
请同学们仿照以上的例子,四人一组讨论回顾已学过的数学规律,用字母表示数的方式把它们表示出来,要求每人说出两例,并在组内交流。每一组派一位代表在全班交流,老师从中选择特别优秀的和有问题的作点评。
三、
拓展练习:
一座楼梯的侧面示意图如图所示
,
要在楼梯上铺一条地毯
,
则地毯至少需多少长
?
若楼梯的宽为
b
,
则地毯的面积为多少
?
四、
课堂总结:
这节课我们学会了什么?(幻灯片出示)
1、
字母可以表示任何数、运算法则、计算公式,数量关系,变化规律……
2
、
数与字母相乘时注意:(
1
)
乘号通常省略;(
2
)
数字写在字母前;(
3
)
带分数化为假分数写在字母前;(
4
)后接单位的相加或相减的式子必须用括号;
(5)
除法运算写成分数形式,除号改为分数线。
五、
布置作业:
1、
必做题:作业本
基础练习
。
2、
选做题:
作业本
综合运用
,书本课后作业题第
5
题。
用字母表示数
教学目标:
通过实例,进一步体验用字母表示数的意义。
理解字母与数一起参与运算的意义。
会利用字母表示数表示简单的数量关系和数学规律。
掌握字母与数一起参与运算时的正确写法。
教学重点:
用字母表示数的意义。
教学难点:
用字母表示数学规律,会用含有字母的式子表示实际问题中的数量关系。
教学过程:
问题引入:
K先生正在看《阿Q正传》,这里K、Q表示什么?字母可表示:人名。
从A地到B地要走3个小时.这里A、B表示什么?字母可表示:地名。
加法交换律:a+b=b+a。字母可表示:运算定律。
设计意图:
情景导入
2016年9月15日,中国在酒泉卫星发射中心用长征二号FT2火箭将天宫二号空间实验室发射升空.它在椭圆形轨道上环绕地球飞过1周,约需90分钟.请问:
(1)绕地球飞行10周约需多少分钟?
(2)绕地球飞行n周约需多少分钟?
设计意图:
知识点一:含字母的式子的书写
例1
用含有字母的式子表示下列数量
练习簿的单价为a元,100本练习簿的总价是100a元。
练习簿的单价为b
元,
a本练习簿的总价是ab元。
练习簿的单价为0.5元,圆珠笔的单价是3.2元,买a本练习簿和b支笔的总价是(0.5a+3.2b)元。
小明的家离学校s千米,小明骑车上学.若每小时行10千米,则需时。
若每斤苹果元,则买m斤苹果需元。
姚明个字高,经测量他通常跨一步的距离1米,若取向前为正,向后为负,那么姚明向前跨a步为a米,向后跨a步为-a米。
例题
判断下列式子书写是否规范,不规范的请改正。
,
,,,
答案:,,,,
知识点二
用含字母的式子表示数量关系
例题
一条河的水流速度是2.5
km/h,船在静水中的速度是
v
km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度?
答案:顺水速度=静水速度+水流速度=(v+2.5)km/h
逆水速度=静水速度-水流速度=(v-2.5)km/h
例题
买一个篮球需要x元,买一个排球需要y元,买一个足球需要
z
元,用式子表示买
3个篮球、5个排球、2个足球共需要的钱数;
解:买3个篮球、5个排球、2个足球共需要(3x+5y+2z)
元
例题
如下图(图中长度单位:cm),用式子表示三角尺的面积;
解:三角尺的面积(单位:)是
例题
如下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积。
这所住宅的建筑面积(单位:)()
归纳:
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言。
要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
理清语句层次明确运算顺序;
牢记一些概念和公式。
练一练
某种商品每袋4.8元,在一个月内的销售量是m
袋,用式子表示在这个月内销售这种商品的收入。
4.8m元
圆柱体的底面半径、高分别是
r,h,用式子表示圆柱体的体积。
有两片棉田,一片有m
(公顷,1
=104
),平均每公顷产棉花a
kg;另一片有n
,平均每公顷产棉花b
kg,用式子表示两片棉田上棉花的总产量。
(am+bn)kg
知识点三
用字母表示规律
如图所示,搭一个正方形需要4根火柴棒。
按上面的方式,搭2个正方形需要7根火柴,搭3个正方形需要10根火柴。搭7个这样的正方形需要22根火柴。
如果用
x
表示所搭正方形的个数,
那么搭
x
个这样的正方形需要多少根火柴?
答:4+3×(x-1)或1+3×x
做一做
根据你的计算方法,搭200个这样的正方形需要601根火柴棒;
搭2017个这样的正方形需要6052根火柴棒。
当堂练习
(1)5箱苹果重m
kg,每箱重kg
;
(2)一个数比a的2倍小5,则这个数为(2a-5);
(3)全校学生总数是x,其中女生占总数52%,则女生人数是0.52x,男生人数是0.48x;
(4)某班有a名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共(4a-25)本。
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号。
科学家爱因斯坦在谈成功的秘诀时,写下了一个公式:A=X+Y+Z,他解释道:A代表成功,X代表艰苦的劳动,
Y代表正确的方法,Z代表少说空话。
讲授新课:
(一)
例题教学
字母还可以表示哪些数呢?学生小组
讨论交流,然后由代表发言。学生会结合自己的生活经验得出字母可以
表示任何数。
师同时说明
利用字母表示
数,能把数和数量关系一般化、简明的表示出来,并
顺势投影显示例题:
例
1
(
1
)练习簿的单价为
a
元,
100
本练习簿的总价是
元。
(
2
)练习簿的单价为
a
元,
b
本练习簿的总价是
元。
(
3
)练习簿的单价为
0.5
元
,
圆珠笔的单价是
3.2
元,买
a
本练习簿和
b
支笔的总价是
元。
(
4
)
练习簿的单价为a元
,
如果买练习簿总共花去了c元,
则买了
本练习簿?
根据总价
=
单价×数量,学生很容易得出。
师在学生回答的基础上进行适当的引导与指点,并指出利用字母表示数时的书写要点。
(二)
练一练:
1
、填空
:⑴、
父亲的年龄比儿子大
28
岁。如果用
x
表示儿子现在的年龄,那么父亲现在的年龄为
岁。(师:后接单位的相加式子要用括号括起来)
⑵、设奶粉每听
p元,橘子每听q元,则买
10
听奶粉、
6
听橘子共需
元。
⑶、长方形的长是
a米,宽是
3
米
,则面积是
平方米,周长是
米。
⑷、小明每时走v千米,
1
时走
千米,
36
分走
千米,
t时走
千米。
(师提醒:带分数与字母相乘是要写成假分数)
⑸、a(a≠
0
)的倒数是
,a的相反数是
。
⑺、面积为
s
的正方形的边长为
。
指学生回答,并要求学生说说你是怎样表示出来的。并
一起总结,然后给出书写时应该注意的事项:
(
1
)
数和表示数的字母相乘,或字母和字母相乘时,乘号可以省略不写,或用“
.
”来代替
;(
2
)
数和字母相乘,在省略乘号时,要把数字写在字母的前面。如
100
×a
可以简写为
100
a
;(
3
)
带分数化为假分数写在字母前;
如
应写成
;
(
4
)后接单位的相加或相减的式子必须用括号;
(5)
除法运算写成分数形式,除号改为分数线
;(
6
)
特别注意:
1
乘以字母时,
1
可以省略不写,如
1
×
a
可写成
a;
-1
乘以字母时,只要在那个字母前加上“
-
”号,
-1
×
a
可写成
-a;
2
、下列表述中,字母各表示什么?
(
1
)圆的面积为
,圆的周长为
2
。
(提醒学生
是圆周率,不是字母
)
(
2
)买
10
件衬衣需
10
s
元。
(
3
)底面积为
50
的长方体的体积为
100
。
(
4
)一条高为
4
的三角形的面积为
2
。
(
5
)教师抽查了班里
学生的作业,共有
本。
(三)合作学习
1
、
师:我们在小学时已经学过一些运算律,你能说出一些运算律吗?(一学生口述运算律,同桌口述用语言文字描述相应的运算律)。
生
1
:加法交换律:交换两个加数的位置,和不变;
生
2
:乘法结合律:三个数相乘,先把前两个数相乘,再乘以第三个数;或者先把后两个数相乘,再乘以第一个数,所得的积不变。
……
师:用语言文字描述运算律比较麻烦,今天我们学习了用字母来表示
数能简明地表示一些数学规律,用字母表示数学规律时,首先要对数学规律的内容充分了解,要表示的数学规律涉及的数量关系是相等关系,还是不等关系;涉及哪些运算;涉及哪些数学符号等。
在师的指导下让学生体会用字母表示学生已学过的运算律并适当的指定并予以表扬、鼓励学生。
2
、
你能用字母表示数来表示下列数学规律吗?
(
1
)互为相反数的两数之和等于
0
。
(
2
)任何一个负数的绝对值大于它本身。
(
3
)一个负数的绝对值等于它的相反数。
(
4
)任何一个不为
0
的数与它的倒数的积等于
1
。
师:互为相反数的两数之和等于
0
,
这
条
数学规律描述的数量关系是相等关系
,
涉及的数学符号
有相反数,涉及的运算有加法,因此
用字母来表示数的方法表示这个数学规律为
(学生自行完成
2
、
3
、
4
小题)
请同学们仿照以上的例子,四人一组讨论回顾已学过的数学规律,用字母表示数的方式把它们表示出来,要求每人说出两例,并在组内交流。每一组派一位代表在全班交流,老师从中选择特别优秀的和有问题的作点评。
三、
拓展练习:
一座楼梯的侧面示意图如图所示
,
要在楼梯上铺一条地毯
,
则地毯至少需多少长
?
若楼梯的宽为
b
,
则地毯的面积为多少
?
四、
课堂总结:
这节课我们学会了什么?(幻灯片出示)
1、
字母可以表示任何数、运算法则、计算公式,数量关系,变化规律……
2
、
数与字母相乘时注意:(
1
)
乘号通常省略;(
2
)
数字写在字母前;(
3
)
带分数化为假分数写在字母前;(
4
)后接单位的相加或相减的式子必须用括号;
(5)
除法运算写成分数形式,除号改为分数线。
五、
布置作业:
1、
必做题:作业本
基础练习
。
2、
选做题:
作业本
综合运用
,书本课后作业题第
5
题。
