苏科版八年级上册数学培优班练习(第4讲): 2.5等腰三角形培优(2)(Word版 无答案)
文档属性
| 名称 | 苏科版八年级上册数学培优班练习(第4讲): 2.5等腰三角形培优(2)(Word版 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 00:00:00 | ||
图片预览

文档简介
八年级数学培优班(第4讲):等腰三角形培优(2)
1.如图,D为等边△ABC的边AB上一点,且DE⊥BC,EF⊥AC,FD⊥AB,垂足分别为点E、F、D.若AB=6,则BE=
.
如图为等边△ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AB=3,
DE=1,则△EFC的面积为
.
3.如图,两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=4,则这两块直角三角板顶点A、A′之间的距离等于
.
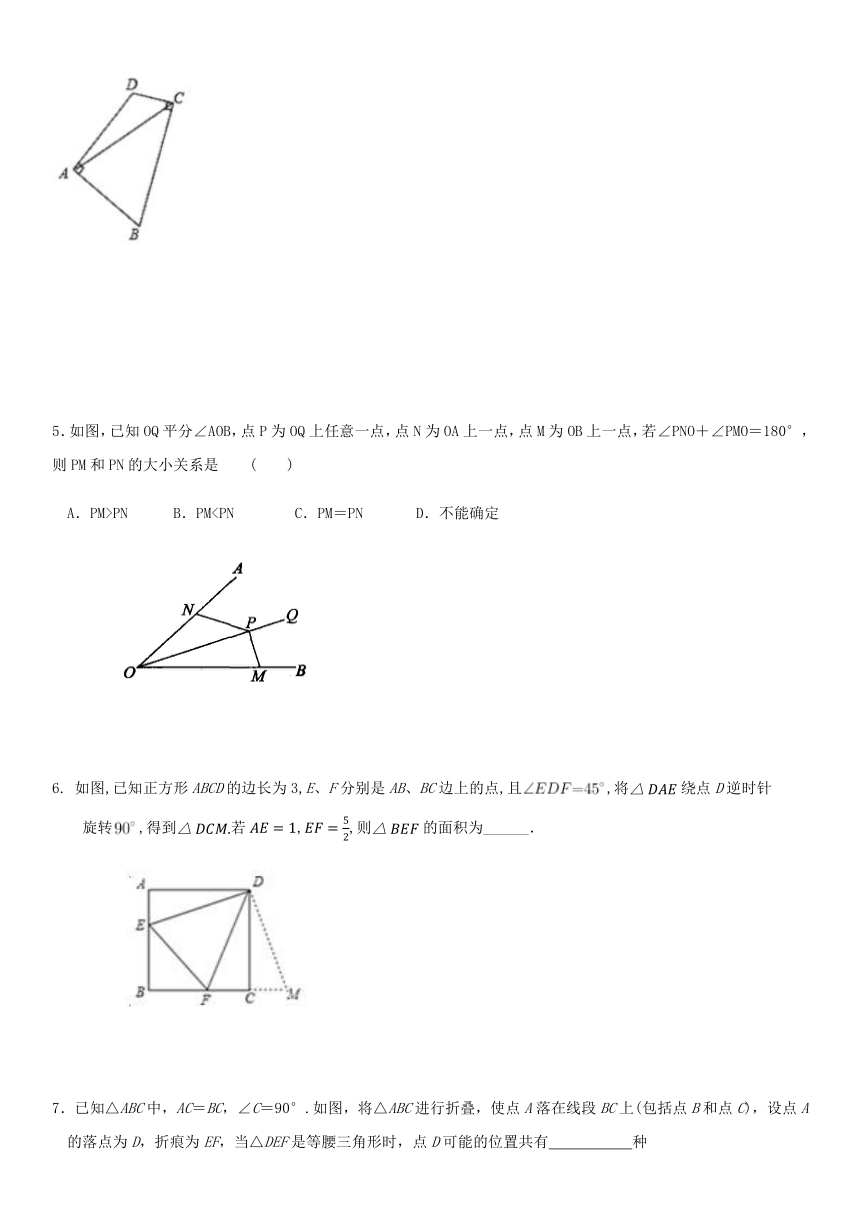
4.如图,四边形中,,连接.若=6,则四边形的面积为
.
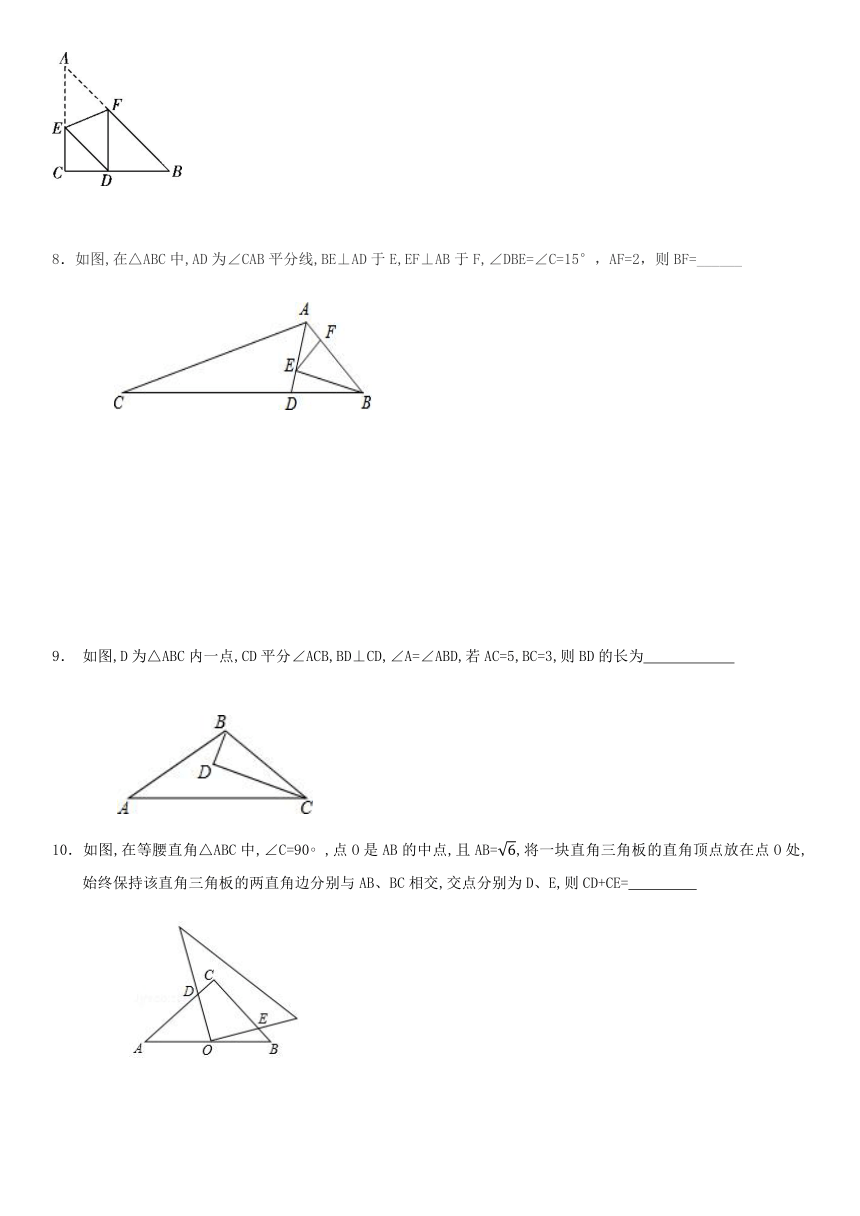
5.如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是
(
)
A.PM>PN
B.PMC.PM=PN
D.不能确定
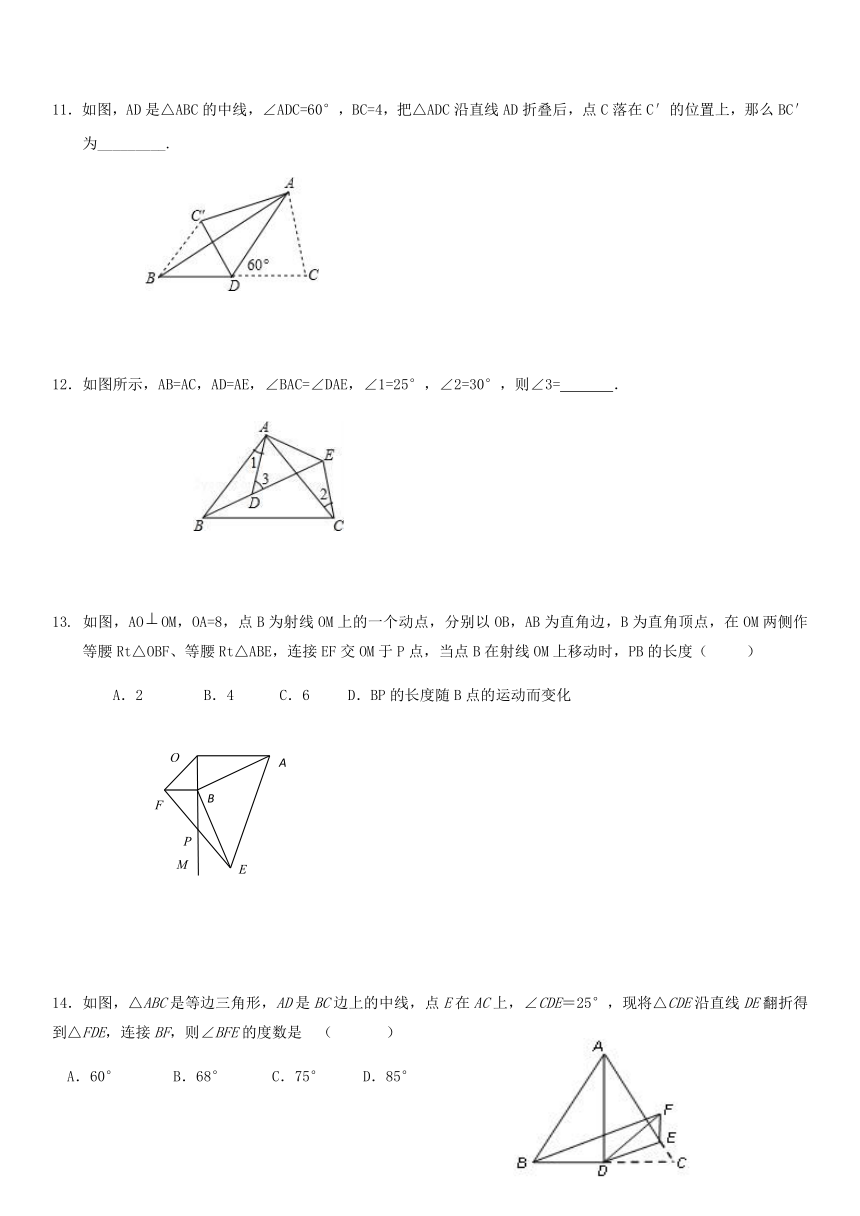
如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且,将绕点D逆时针
旋转,得到若,,则的面积为______.
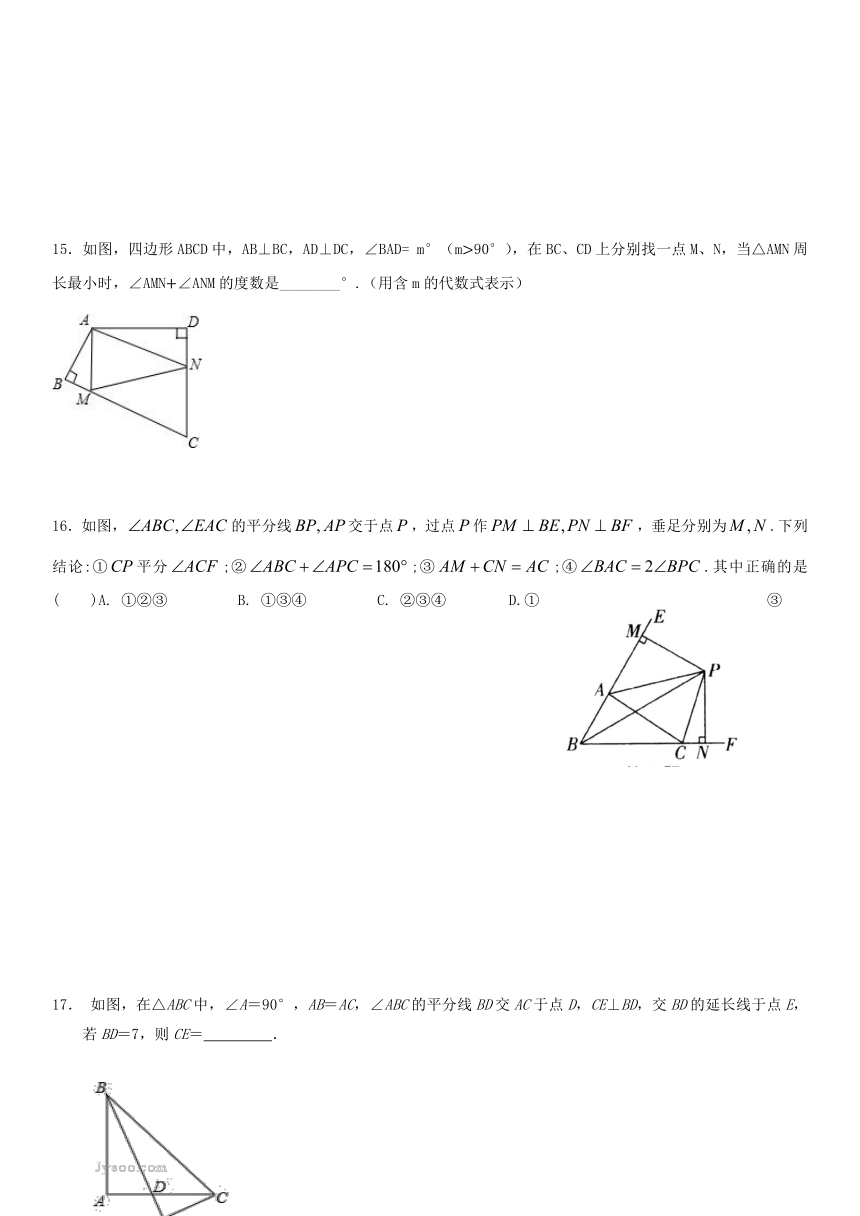
7.已知△ABC中,AC=BC,∠C=90°.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有
种
8.如图,在△ABC中,AD为∠CAB平分线,BE⊥AD于E,EF⊥AB于F,∠DBE=∠C=15°,AF=2,则BF=______
9.
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为
10.如图,在等腰直角△ABC中,∠C=90?,点O是AB的中点,且AB=,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=
11.如图,AD是△ABC的中线,∠ADC=60°,BC=4,把△ADC沿直线AD折叠后,点C落在C′的位置上,那么BC′为_________.
12.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=
.
13.
如图,AOOM,OA=8,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度(
)
A.2
B.4
C.6
D.BP的长度随B点的运动而变化
如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将△CDE沿直线DE翻折得到△FDE,连接BF,则∠BFE的度数是
(
)
A.60°
B.68°
C.75°
D.85°
15.如图,四边形ABCD中,AB⊥BC,AD⊥DC,∠BAD=
m°(m90°),在BC、CD上分别找一点M、N,当△AMN周长最小时,∠AMN∠ANM的度数是________°.(用含m的代数式表示)
16.如图,的平分线交于点,过点作,垂足分别为.下列结论:①平分;②;③;④.其中正确的是(
)A.
①②③
B.
①③④
C.
②③④
D.①③
17.
如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=7,则CE=
.
18.如图,已知,BD为的角平分线,且,E为BD延长线上的一点,下列结论:≌;;;其中正确的有
个
已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;
④S△ABC=S四边形AOCP.其中正确的有
(填序号)
20.如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是
.
21.如图,在Rt△ABC中,∠ACB=90°,,,是的角平分线,若点、分别是线段和边上的动点,则的最小值是
▲
.
22.如图,在△ABC中,AB=AC,BC=4,面积是12,AC的垂直平分线EF分别交AB,AC边于点E,F.
若点D为BC边的中点,点P为线段EF上一动点,则△PCD周长的最小值为?______?.?
??
23.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)在运动过程中线段ED的长是否发生变化?
如果不变,求出线段ED的长;如果变化请说明理由.
24.如图,
已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动)
.
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图②证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立?请直接写出结论,不必证明或说明理由.
25、(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
数学课上,李老师出示了如下框中的题目.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况?探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE
_______DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE
____-DB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,
求
CD的长(请你直接写出结果).
1.如图,D为等边△ABC的边AB上一点,且DE⊥BC,EF⊥AC,FD⊥AB,垂足分别为点E、F、D.若AB=6,则BE=
.
如图为等边△ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AB=3,
DE=1,则△EFC的面积为
.
3.如图,两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=4,则这两块直角三角板顶点A、A′之间的距离等于
.
4.如图,四边形中,,连接.若=6,则四边形的面积为
.
5.如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是
(
)
A.PM>PN
B.PM
D.不能确定
如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且,将绕点D逆时针
旋转,得到若,,则的面积为______.
7.已知△ABC中,AC=BC,∠C=90°.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有
种
8.如图,在△ABC中,AD为∠CAB平分线,BE⊥AD于E,EF⊥AB于F,∠DBE=∠C=15°,AF=2,则BF=______
9.
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为
10.如图,在等腰直角△ABC中,∠C=90?,点O是AB的中点,且AB=,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=
11.如图,AD是△ABC的中线,∠ADC=60°,BC=4,把△ADC沿直线AD折叠后,点C落在C′的位置上,那么BC′为_________.
12.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=
.
13.
如图,AOOM,OA=8,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度(
)
A.2
B.4
C.6
D.BP的长度随B点的运动而变化
如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将△CDE沿直线DE翻折得到△FDE,连接BF,则∠BFE的度数是
(
)
A.60°
B.68°
C.75°
D.85°
15.如图,四边形ABCD中,AB⊥BC,AD⊥DC,∠BAD=
m°(m90°),在BC、CD上分别找一点M、N,当△AMN周长最小时,∠AMN∠ANM的度数是________°.(用含m的代数式表示)
16.如图,的平分线交于点,过点作,垂足分别为.下列结论:①平分;②;③;④.其中正确的是(
)A.
①②③
B.
①③④
C.
②③④
D.①③
17.
如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=7,则CE=
.
18.如图,已知,BD为的角平分线,且,E为BD延长线上的一点,下列结论:≌;;;其中正确的有
个
已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;
④S△ABC=S四边形AOCP.其中正确的有
(填序号)
20.如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是
.
21.如图,在Rt△ABC中,∠ACB=90°,,,是的角平分线,若点、分别是线段和边上的动点,则的最小值是
▲
.
22.如图,在△ABC中,AB=AC,BC=4,面积是12,AC的垂直平分线EF分别交AB,AC边于点E,F.
若点D为BC边的中点,点P为线段EF上一动点,则△PCD周长的最小值为?______?.?
??
23.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)在运动过程中线段ED的长是否发生变化?
如果不变,求出线段ED的长;如果变化请说明理由.
24.如图,
已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动)
.
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图②证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立?请直接写出结论,不必证明或说明理由.
25、(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
数学课上,李老师出示了如下框中的题目.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况?探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE
_______DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE
____-DB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,
求
CD的长(请你直接写出结果).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
