26.2锐角三角函数的计算-冀教版九年级数学上册课件(18张)
文档属性
| 名称 | 26.2锐角三角函数的计算-冀教版九年级数学上册课件(18张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 09:21:09 | ||
图片预览




文档简介
(共18张PPT)
26.2
锐角三角函数的计算
冀教版九上
第二十六章
解直角三角形
新课引入
新课学习
典例精析
测试小结
学
习
目
标
冀教版九上
1.复习并巩固锐角三角形函数的相关知识.
2.学会利用计算器求三角函数值并进行相关计算.
3.学会利用计算器根据三角函数值求锐角度数并计算.
旧知链接
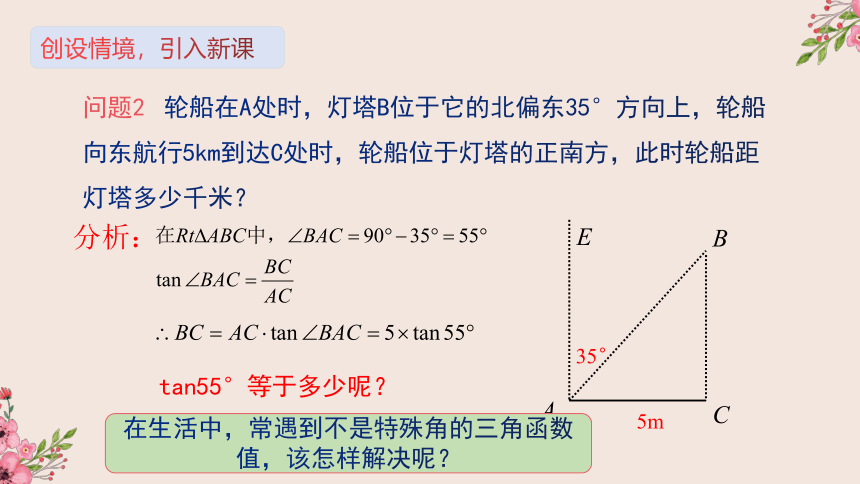
填写下表:
锐角α
三角函数
30°
45°
60°
sin
α
cos
α
tan
α
创设情境,引入新课
D
A
B
E
1.6m
10m
60°
C
问题1
升国旗时,小明站在操场上离国旗10m处行注目礼.当国旗升至顶端时,小明看国旗视线的仰角为60°(如图所示),若小明双眼离地面1.60m,你能帮助小明求出旗杆AB的高度吗?
分析:
创设情境,引入新课
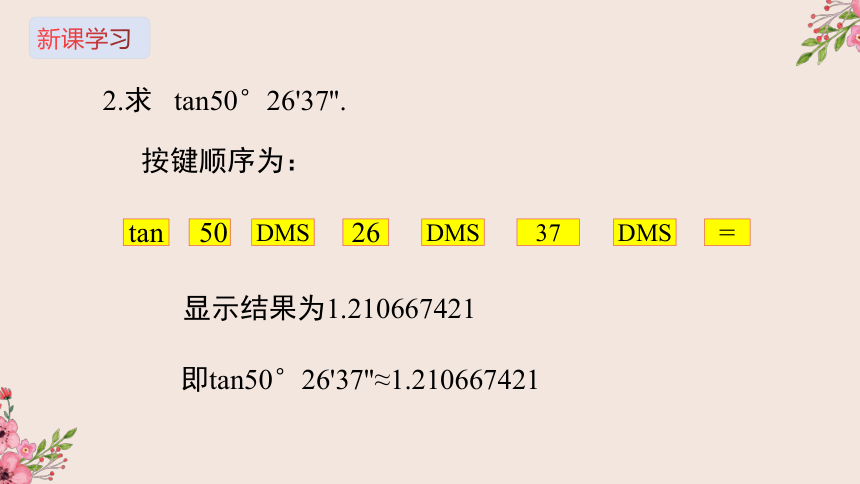
问题2
轮船在A处时,灯塔B位于它的北偏东35°方向上,轮船向东航行5km到达C处时,轮船位于灯塔的正南方,此时轮船距灯塔多少千米?
A
B
E
5m
35°
C
分析:
在生活中,常遇到不是特殊角的三角函数值,该怎样解决呢?
tan55°等于多少呢?
新课学习
一、用计算器求三角函数值
1.求sin36°.
第一步:按计算器
键,
sin
第二步:输入角度值36,
屏幕显示结果sin36°=0.587785252
(注意:也有的计算器是先输入角度再按函数名称键).
新课学习
2.求
tan50°26'37''.
按键顺序为:
tan
50
DMS
26
=
DMS
37
DMS
显示结果为1.210667421
即tan50°26'37''≈1.210667421
巩固小练习
解决前置中的问题二,求出轮船距灯塔多少千米?
利用计算器得到tan55°≈1.428
∴BC=5×1.428=7.14
∴轮船距灯塔约7.14千米.
分析:
新课学习
二、利用计算器求锐角的度数
如果已知锐角三角函数值,也可以使用计算器求出相应的锐角.
新课学习
例1.用计算器求下列锐角的度数:(结果精确到1'')
解:按键顺序:
显示结果为58.41923095
若将其化为度、分、秒表示,可继续按键:
(1)若cosα=0.5237,求锐角α.
2nd
F
2ndF
0
.
=
5
2
3
7
DEG
显示结果为58
25
9.23,即α≈58°25'9''
新课学习
例1.用计算器求下列锐角的度数:(结果精确到1'')
解:按键顺序:
显示结果为58.75078643
若将其化为度、分、秒表示,可继续按键:
(2)若tanβ
=1.6480,求锐角β.
2nd
F
2ndF
1
.
=
6
4
8
0
DEG
显示结果为58
45
2.83,即β≈58°45'3''
巩固小练习
1.Rt△ABC中,∠C=90°,BC:AC=3:4,运用计算器计算,∠A的度数约为(精确到1°)______.
2.sinα=0.2,cosβ=0.8,则α+β=______.
37°
48°24'
拓展探索
1.用计算器求下列锐角三角函数值;
(1)
sin20°=
,
cos70°=
;
(2)tan3°8
'
=
,tan80°25'43″=
.
sin35°=
,cos55°=
;
sin15°32
'
=
,cos74°28
'
=
.
观察题中的数
据验证了与三
角函数有关的
哪些结论?
0.342
0.342
0.574
0.268
0.574
0.268
5.930
0.055
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
拓展探索
课堂小测
1.
已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.627
5,sinB=0.054
7;
(2)cosA=0.625
2,cosB=0.165
9;
(3)tanA=4.842
5,tanB=0.881
6.
∠B=38°8″
∠A=38°51′57″
∠A=51°18′11″
∠B=80°27′2″
∠A=78°19′58″
∠B=41°23′58″
创设情境,引入新课
A
2.下列各式中一定成立的是(
)
A.tan75°﹥tan48°﹥tan15°
B.
tan75°﹤tan48°﹤tan15°
C.
cos75°﹥cos48°﹥cos15°
D.
sin75°﹤sin48°课堂小结
1.我们可以用计算器求锐角三角函数值.
2.已知锐角三角函数值,可以用计算器求其相应的锐角.
3.正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
同学们再见
26.2
锐角三角函数的计算
冀教版九上
第二十六章
解直角三角形
新课引入
新课学习
典例精析
测试小结
学
习
目
标
冀教版九上
1.复习并巩固锐角三角形函数的相关知识.
2.学会利用计算器求三角函数值并进行相关计算.
3.学会利用计算器根据三角函数值求锐角度数并计算.
旧知链接
填写下表:
锐角α
三角函数
30°
45°
60°
sin
α
cos
α
tan
α
创设情境,引入新课
D
A
B
E
1.6m
10m
60°
C
问题1
升国旗时,小明站在操场上离国旗10m处行注目礼.当国旗升至顶端时,小明看国旗视线的仰角为60°(如图所示),若小明双眼离地面1.60m,你能帮助小明求出旗杆AB的高度吗?
分析:
创设情境,引入新课
问题2
轮船在A处时,灯塔B位于它的北偏东35°方向上,轮船向东航行5km到达C处时,轮船位于灯塔的正南方,此时轮船距灯塔多少千米?
A
B
E
5m
35°
C
分析:
在生活中,常遇到不是特殊角的三角函数值,该怎样解决呢?
tan55°等于多少呢?
新课学习
一、用计算器求三角函数值
1.求sin36°.
第一步:按计算器
键,
sin
第二步:输入角度值36,
屏幕显示结果sin36°=0.587785252
(注意:也有的计算器是先输入角度再按函数名称键).
新课学习
2.求
tan50°26'37''.
按键顺序为:
tan
50
DMS
26
=
DMS
37
DMS
显示结果为1.210667421
即tan50°26'37''≈1.210667421
巩固小练习
解决前置中的问题二,求出轮船距灯塔多少千米?
利用计算器得到tan55°≈1.428
∴BC=5×1.428=7.14
∴轮船距灯塔约7.14千米.
分析:
新课学习
二、利用计算器求锐角的度数
如果已知锐角三角函数值,也可以使用计算器求出相应的锐角.
新课学习
例1.用计算器求下列锐角的度数:(结果精确到1'')
解:按键顺序:
显示结果为58.41923095
若将其化为度、分、秒表示,可继续按键:
(1)若cosα=0.5237,求锐角α.
2nd
F
2ndF
0
.
=
5
2
3
7
DEG
显示结果为58
25
9.23,即α≈58°25'9''
新课学习
例1.用计算器求下列锐角的度数:(结果精确到1'')
解:按键顺序:
显示结果为58.75078643
若将其化为度、分、秒表示,可继续按键:
(2)若tanβ
=1.6480,求锐角β.
2nd
F
2ndF
1
.
=
6
4
8
0
DEG
显示结果为58
45
2.83,即β≈58°45'3''
巩固小练习
1.Rt△ABC中,∠C=90°,BC:AC=3:4,运用计算器计算,∠A的度数约为(精确到1°)______.
2.sinα=0.2,cosβ=0.8,则α+β=______.
37°
48°24'
拓展探索
1.用计算器求下列锐角三角函数值;
(1)
sin20°=
,
cos70°=
;
(2)tan3°8
'
=
,tan80°25'43″=
.
sin35°=
,cos55°=
;
sin15°32
'
=
,cos74°28
'
=
.
观察题中的数
据验证了与三
角函数有关的
哪些结论?
0.342
0.342
0.574
0.268
0.574
0.268
5.930
0.055
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
拓展探索
课堂小测
1.
已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.627
5,sinB=0.054
7;
(2)cosA=0.625
2,cosB=0.165
9;
(3)tanA=4.842
5,tanB=0.881
6.
∠B=38°8″
∠A=38°51′57″
∠A=51°18′11″
∠B=80°27′2″
∠A=78°19′58″
∠B=41°23′58″
创设情境,引入新课
A
2.下列各式中一定成立的是(
)
A.tan75°﹥tan48°﹥tan15°
B.
tan75°﹤tan48°﹤tan15°
C.
cos75°﹥cos48°﹥cos15°
D.
sin75°﹤sin48°
1.我们可以用计算器求锐角三角函数值.
2.已知锐角三角函数值,可以用计算器求其相应的锐角.
3.正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
