第23章数据分析复习与小结-冀教版九年级数学上册课件(共26张ppt)
文档属性
| 名称 | 第23章数据分析复习与小结-冀教版九年级数学上册课件(共26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
复习与小结
冀教版九上
第二十三章
数据分析
学习目标
3.掌握用样本估计总体的统计思想.
2.会选择合适的统计量表示数据、分析数据.
1.理解平均数、中位数、众数、方差的意义,并能熟练计算.
冀教版九上
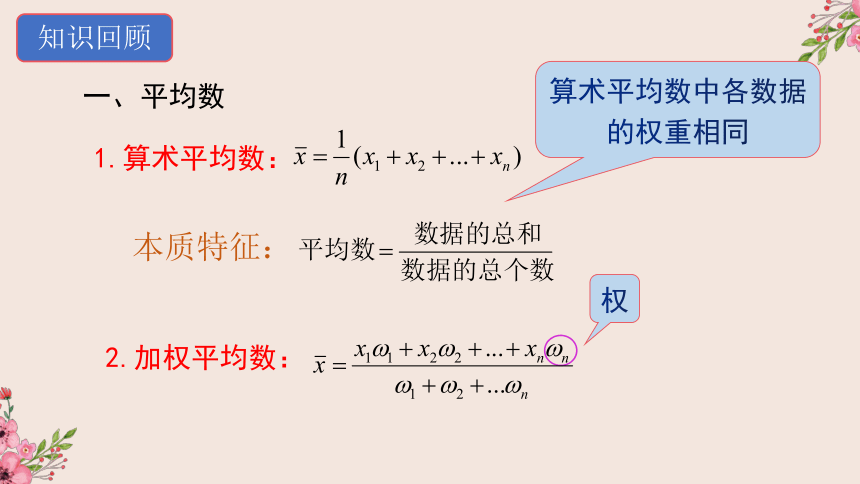
知识回顾
一、平均数
1.算术平均数:
本质特征:
2.加权平均数:
算术平均数中各数据的权重相同
权
知识回顾
1.一般情况下,可以选择用平均数代表一组数据,但当数据中出现极端值时,或者说数据的波动比较大时,平均数不再适合作为数据的代表.
2.在一组数据中,平均数是唯一的,平均数不一定是这组数据中的一个数.
注意:
知识运用
1.周日,小明和同学一起去爬山,他们上山的速度是3km/h,沿原路下山的速度是5km/h,求他们的上山、下山的平均速度.
答:他们上山、下山的平均速度是3.75km/h.
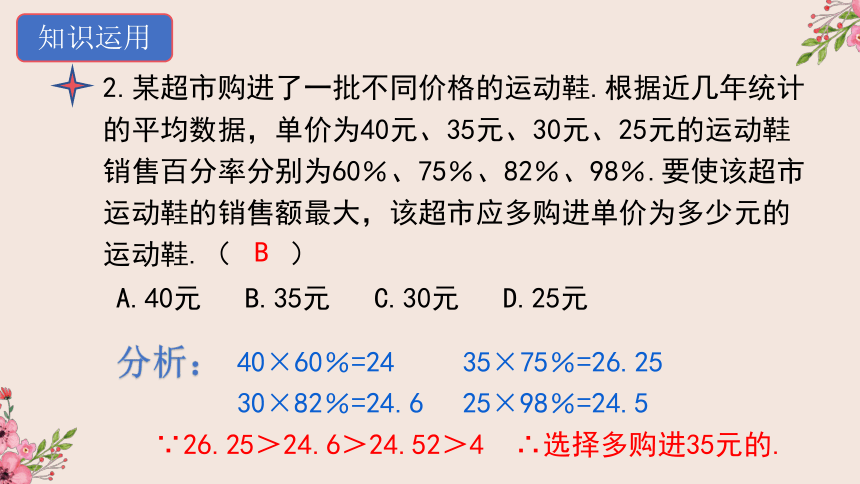
知识运用
2.某超市购进了一批不同价格的运动鞋.根据近几年统计的平均数据,单价为40元、35元、30元、25元的运动鞋销售百分率分别为60%、75%、82%、98%.要使该超市运动鞋的销售额最大,该超市应多购进单价为多少元的运动鞋.(
)
A.40元
B.35元
C.30元
D.25元
40×60%=24
35×75%=26.25
30×82%=24.6
25×98%=24.5
分析:
∵26.25>24.6>24.52>4
∴选择多购进35元的.
B
知识运用
分析:
5
结论:当一组数据中的每个数据都加、减、乘、除以a(a≠0)时,由此产生的新数据的平均数就由原数据的平均数加、
减、乘、除以a得到.
知识回顾
二、中位数和众数
1.中位数
一般地,将n个数按大小顺序排列,如果n为奇数,那么就把处于中间位置的数据叫做这组数据的中位数;如果n为偶数,那么把处于中间位置的两个数据的平均数叫做这组数据的中位数.
知识回顾
2.众数
注意:
一般地,把一组数据中出现次数最多的那个数据叫做众数.一组数据的众数可以是一个、多个或没有.
一组数据的众数一定是这组数据中的数.
一组数据的中位数不一定是这组数据中的数,但一组数据的中位数是唯一的.
知识运用
1.已知一组数据3,5,6,7,5.则其平均数为_____;
中位数是______;众数是_____.
2.某校4个绿化小组一天的植树棵树如下:8,10,x,10,已知这组数据的众数与平均数相同,则这组数据的中位数是(
).
分析:
①由于一组数据的平均数是唯一的,因此可得这组数据的众数是唯一的,为10.
②(8+10+x+10)÷4=10.可得x=12.
③将这4个数按大小排序为8,10,10,12.因此中位数为10.
5.2
5
5
10
知识运用
C
3.如图为某班35名学生投篮成绩的条形统计图,其中上面部分数据破损导致数据不完全,已知此班学生投篮成绩的中位数是5.则根据图形无法确定下列哪一选项中的数值.(
)
0
2
4
6
8
10
A.4球以下的人数
B.5球以下的人数
C.6球以下的人数
D.7球以下的人数
1
2
3
4
5
6
7
投篮成绩
人数
知识回顾
三、方差
1.概念:
一组数据中各个数据与平均数偏差的平方的平均数,叫做这组数据的方差.
2.公式:
数据分布较分散时,方差较大;数据分布较集中时,方差较小.方差大小反映了数据波动的大小.
3.结论:
4.注意:
两组数据在平均数相当的前提下,比较方差才有意义.
知识运用
1.一组数据6,4,a,3,2的平均数是4,则这组数据的方差为____.
2.学校为了选拔4名播音员,对20名学生进行了两次普通话测试,满分为10分.统计得,第一次测试的方差为1.2275分?,第二次方差为1.3475分?.则第___次的测试结果对选拔播音员更要参考意义.
2
二
方差大时对于选拔更有参考意义
知识运用
3.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数和方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择____.
185
3.6
180
3.6
乙
甲
丙
丁
平均数(cm)
方差(cm?)
180
185
7.4
8.1
甲
平均数相当时,方差小的数据更稳定
知识运用
分析:
当一组数据中的每个数据都乘以a(a≠0)时,则得到的新数据的方差等于原数据方差的a?倍.
当一组数据中的每个数据都加或减同一个数时,则得到的新数据的方差等于原数据方差.
∴新数据的方差=3×2?=12
12
知识回顾
四、用样本估计总体
1.在实际生活中,由于普查的局限性,更多的时候,人们会选择用抽样调查统计数据.
2.当样本容量增大时,样本的平均数的波动变小,逐渐趋于稳定,且与总体平均数比较接近.因此,实际生活中,常用样本平均数估计总体平均数,也用样本方差估计总体方差.
知识运用
1.生物工作者为了估计小山上山雀的数量,先捕了20只做上标记后放还,一星期后,又捕捉了40只山雀,发现带标记的有2只,由此估计小山上的山雀有____只.
一星期后捕捉的40只山雀是一个样本.样本中带标记的山雀所占的比例为5%,则估计总体中,带标记的山雀所占的比例也是5%.
400
20÷5%=400
分析:
用样本的百分比估计总体的百分比
知识运用
2.从一个鱼塘打捞出200尾鲤鱼,为了估计这些鲤鱼的总质量,从中任意选择了6尾,称出它们的质量(单位:kg)分别为1.6,1.4,1.2,1.7,1.8,1.3,估计这200尾鲤鱼的总质量大约是______kg.
300
用样本的平均数估计总体的平均数
综合练习
1.5名学生投篮球,规定每人投20次,统计他们每人投中的次数,得到5个数据.若这5个数据的中位数是6,唯一的众数是7,则他们投中次数的总和可能是(
).
A.20
B.28
C.30
D.31
B
综合练习
2.某设计队为了解运动员的年龄情况,做了一次年龄调查.根据射击运动员的年龄(单位:岁),绘制了如下图所示的统计图.
(1)你能利用统计图求出平均数、众数、中位数中的哪些统计量?并直接写出结果.
13岁10%
14岁30%
15岁25%
16岁m%
17岁15%
众数:14岁
中位数:15岁
m%=1-10%-30%-25%-15%=20%
平均数=13×10%+14×30%+15×25%+16×20%+17×15%=15(岁)
综合练习
2.某射计队为了解运动员的年龄情况,做了一次年龄调查.根据射击运动员的年龄(单位:岁),绘制了如下图所示的统计图.
(2)小颖认为,若从该射击队中任意挑选四名队员,则必有一名队员的年龄是15岁.你认为她的判断正确吗?
13岁10%
14岁30%
15岁25%
16岁m%
17岁15%
不正确.从扇形图中不能得出射击队的具体人数,因此不能因为15岁所占的比例为四分之一,就认为挑选的4人中,一定有15岁的.
综合练习
2.某设计队为了解运动员的年龄情况,做了一次年龄调查.根据射击运动员的年龄(单位:岁),绘制了如下图所示的统计图.
(3)小亮认为,可以统计图求出方差.你认同吗?
13岁10%
14岁30%
15岁25%
16岁m%
17岁15%
认同
设有n个运动员.
S?=[10%·n(13-15)?+30%·n(14-15)?+25%·n(15-15)?+20%·n(16-15)?+15%·n(17-15)?]÷n=1.5(岁?)
综合练习
3.甲校和乙校九年级学生各有300名.为了解这两个学校九年级学生的英语单词掌握情况,进行了抽样调查,过程如下:
①收集数据.从两个学校九年级中各随机抽取10名学生,进行英语单词测试.成绩如下:(百分制,单位:分)
甲校:92
100
86
89
73
98
54
95
98
85
乙校:100
100
94
83
74
86
75
100
73
75
②根据数据,填写下表:
87
90.5
86
中位数/分
平均数/分
众数/分
方差/分?
甲校
179.4
121.6
学校
乙校
84.5
98
100
综合练习
(1)若成绩90分以上为优秀估计乙校九年级学生英语单词掌握优秀的人数.
300×40%=120
分析:
样本容量为10的样本中,优秀的人数为4,可得样本中的优秀率为40%,据此推断总体中优秀率为40%.
因此乙校九年级学生英语单词掌握优秀的人数为120.
综合练习
(2)你认为那个学校的九年级学生英语单词掌握得比较好?说明你的理由.(至少从两个不同的角度说明推断的合理性).
乙校的九年级学生英语单词掌握得比较好.
理由:①乙校的九年级学生英语单词测试中,平均分高于甲校;②乙校的九年级学生在英语单词测试中,中位数较高,说明乙校英语单词测试成绩分数高的学生较多.
(答案不唯一).
同学们再见
复习与小结
冀教版九上
第二十三章
数据分析
学习目标
3.掌握用样本估计总体的统计思想.
2.会选择合适的统计量表示数据、分析数据.
1.理解平均数、中位数、众数、方差的意义,并能熟练计算.
冀教版九上
知识回顾
一、平均数
1.算术平均数:
本质特征:
2.加权平均数:
算术平均数中各数据的权重相同
权
知识回顾
1.一般情况下,可以选择用平均数代表一组数据,但当数据中出现极端值时,或者说数据的波动比较大时,平均数不再适合作为数据的代表.
2.在一组数据中,平均数是唯一的,平均数不一定是这组数据中的一个数.
注意:
知识运用
1.周日,小明和同学一起去爬山,他们上山的速度是3km/h,沿原路下山的速度是5km/h,求他们的上山、下山的平均速度.
答:他们上山、下山的平均速度是3.75km/h.
知识运用
2.某超市购进了一批不同价格的运动鞋.根据近几年统计的平均数据,单价为40元、35元、30元、25元的运动鞋销售百分率分别为60%、75%、82%、98%.要使该超市运动鞋的销售额最大,该超市应多购进单价为多少元的运动鞋.(
)
A.40元
B.35元
C.30元
D.25元
40×60%=24
35×75%=26.25
30×82%=24.6
25×98%=24.5
分析:
∵26.25>24.6>24.52>4
∴选择多购进35元的.
B
知识运用
分析:
5
结论:当一组数据中的每个数据都加、减、乘、除以a(a≠0)时,由此产生的新数据的平均数就由原数据的平均数加、
减、乘、除以a得到.
知识回顾
二、中位数和众数
1.中位数
一般地,将n个数按大小顺序排列,如果n为奇数,那么就把处于中间位置的数据叫做这组数据的中位数;如果n为偶数,那么把处于中间位置的两个数据的平均数叫做这组数据的中位数.
知识回顾
2.众数
注意:
一般地,把一组数据中出现次数最多的那个数据叫做众数.一组数据的众数可以是一个、多个或没有.
一组数据的众数一定是这组数据中的数.
一组数据的中位数不一定是这组数据中的数,但一组数据的中位数是唯一的.
知识运用
1.已知一组数据3,5,6,7,5.则其平均数为_____;
中位数是______;众数是_____.
2.某校4个绿化小组一天的植树棵树如下:8,10,x,10,已知这组数据的众数与平均数相同,则这组数据的中位数是(
).
分析:
①由于一组数据的平均数是唯一的,因此可得这组数据的众数是唯一的,为10.
②(8+10+x+10)÷4=10.可得x=12.
③将这4个数按大小排序为8,10,10,12.因此中位数为10.
5.2
5
5
10
知识运用
C
3.如图为某班35名学生投篮成绩的条形统计图,其中上面部分数据破损导致数据不完全,已知此班学生投篮成绩的中位数是5.则根据图形无法确定下列哪一选项中的数值.(
)
0
2
4
6
8
10
A.4球以下的人数
B.5球以下的人数
C.6球以下的人数
D.7球以下的人数
1
2
3
4
5
6
7
投篮成绩
人数
知识回顾
三、方差
1.概念:
一组数据中各个数据与平均数偏差的平方的平均数,叫做这组数据的方差.
2.公式:
数据分布较分散时,方差较大;数据分布较集中时,方差较小.方差大小反映了数据波动的大小.
3.结论:
4.注意:
两组数据在平均数相当的前提下,比较方差才有意义.
知识运用
1.一组数据6,4,a,3,2的平均数是4,则这组数据的方差为____.
2.学校为了选拔4名播音员,对20名学生进行了两次普通话测试,满分为10分.统计得,第一次测试的方差为1.2275分?,第二次方差为1.3475分?.则第___次的测试结果对选拔播音员更要参考意义.
2
二
方差大时对于选拔更有参考意义
知识运用
3.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数和方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择____.
185
3.6
180
3.6
乙
甲
丙
丁
平均数(cm)
方差(cm?)
180
185
7.4
8.1
甲
平均数相当时,方差小的数据更稳定
知识运用
分析:
当一组数据中的每个数据都乘以a(a≠0)时,则得到的新数据的方差等于原数据方差的a?倍.
当一组数据中的每个数据都加或减同一个数时,则得到的新数据的方差等于原数据方差.
∴新数据的方差=3×2?=12
12
知识回顾
四、用样本估计总体
1.在实际生活中,由于普查的局限性,更多的时候,人们会选择用抽样调查统计数据.
2.当样本容量增大时,样本的平均数的波动变小,逐渐趋于稳定,且与总体平均数比较接近.因此,实际生活中,常用样本平均数估计总体平均数,也用样本方差估计总体方差.
知识运用
1.生物工作者为了估计小山上山雀的数量,先捕了20只做上标记后放还,一星期后,又捕捉了40只山雀,发现带标记的有2只,由此估计小山上的山雀有____只.
一星期后捕捉的40只山雀是一个样本.样本中带标记的山雀所占的比例为5%,则估计总体中,带标记的山雀所占的比例也是5%.
400
20÷5%=400
分析:
用样本的百分比估计总体的百分比
知识运用
2.从一个鱼塘打捞出200尾鲤鱼,为了估计这些鲤鱼的总质量,从中任意选择了6尾,称出它们的质量(单位:kg)分别为1.6,1.4,1.2,1.7,1.8,1.3,估计这200尾鲤鱼的总质量大约是______kg.
300
用样本的平均数估计总体的平均数
综合练习
1.5名学生投篮球,规定每人投20次,统计他们每人投中的次数,得到5个数据.若这5个数据的中位数是6,唯一的众数是7,则他们投中次数的总和可能是(
).
A.20
B.28
C.30
D.31
B
综合练习
2.某设计队为了解运动员的年龄情况,做了一次年龄调查.根据射击运动员的年龄(单位:岁),绘制了如下图所示的统计图.
(1)你能利用统计图求出平均数、众数、中位数中的哪些统计量?并直接写出结果.
13岁10%
14岁30%
15岁25%
16岁m%
17岁15%
众数:14岁
中位数:15岁
m%=1-10%-30%-25%-15%=20%
平均数=13×10%+14×30%+15×25%+16×20%+17×15%=15(岁)
综合练习
2.某射计队为了解运动员的年龄情况,做了一次年龄调查.根据射击运动员的年龄(单位:岁),绘制了如下图所示的统计图.
(2)小颖认为,若从该射击队中任意挑选四名队员,则必有一名队员的年龄是15岁.你认为她的判断正确吗?
13岁10%
14岁30%
15岁25%
16岁m%
17岁15%
不正确.从扇形图中不能得出射击队的具体人数,因此不能因为15岁所占的比例为四分之一,就认为挑选的4人中,一定有15岁的.
综合练习
2.某设计队为了解运动员的年龄情况,做了一次年龄调查.根据射击运动员的年龄(单位:岁),绘制了如下图所示的统计图.
(3)小亮认为,可以统计图求出方差.你认同吗?
13岁10%
14岁30%
15岁25%
16岁m%
17岁15%
认同
设有n个运动员.
S?=[10%·n(13-15)?+30%·n(14-15)?+25%·n(15-15)?+20%·n(16-15)?+15%·n(17-15)?]÷n=1.5(岁?)
综合练习
3.甲校和乙校九年级学生各有300名.为了解这两个学校九年级学生的英语单词掌握情况,进行了抽样调查,过程如下:
①收集数据.从两个学校九年级中各随机抽取10名学生,进行英语单词测试.成绩如下:(百分制,单位:分)
甲校:92
100
86
89
73
98
54
95
98
85
乙校:100
100
94
83
74
86
75
100
73
75
②根据数据,填写下表:
87
90.5
86
中位数/分
平均数/分
众数/分
方差/分?
甲校
179.4
121.6
学校
乙校
84.5
98
100
综合练习
(1)若成绩90分以上为优秀估计乙校九年级学生英语单词掌握优秀的人数.
300×40%=120
分析:
样本容量为10的样本中,优秀的人数为4,可得样本中的优秀率为40%,据此推断总体中优秀率为40%.
因此乙校九年级学生英语单词掌握优秀的人数为120.
综合练习
(2)你认为那个学校的九年级学生英语单词掌握得比较好?说明你的理由.(至少从两个不同的角度说明推断的合理性).
乙校的九年级学生英语单词掌握得比较好.
理由:①乙校的九年级学生英语单词测试中,平均分高于甲校;②乙校的九年级学生在英语单词测试中,中位数较高,说明乙校英语单词测试成绩分数高的学生较多.
(答案不唯一).
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
