第28章元复习与小结-冀教版九年级数学上册课件(共28张ppt)
文档属性
| 名称 | 第28章元复习与小结-冀教版九年级数学上册课件(共28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
复习与小结
冀教版九上
第二十八章
圆
学习目标
3.熟练运用弧长、扇形面积公式进行计算.
2.会用圆的有关性质,并掌握圆中常用的辅助线的作法.
1.熟记圆中的相关概念.
冀教版九上
知识回顾
一、圆的概念及性质
1.圆:
2.弦:
到定点的距离等于定长的所有点组成的图形.
确定圆的条件:圆心和半径.
圆上任意两点间的线段.
直径是圆中最长的弦.
知识回顾
一、圆的概念及性质
3.弧:
4.等圆:
圆上任意两点间的部分.
圆上的弧包括:优弧、半圆、劣弧.
能够完全重合的两个圆.
等弧只存在与同圆或等圆中.
5.等弧:
能够完全重合的两条弧.
知识回顾
一、圆的概念及性质
圆的对称性
1.圆是轴对称图形,对称轴是过圆心的直线,圆有无数条对称轴.
2.圆是中心对称图形,对称中心是圆心.
知识运用
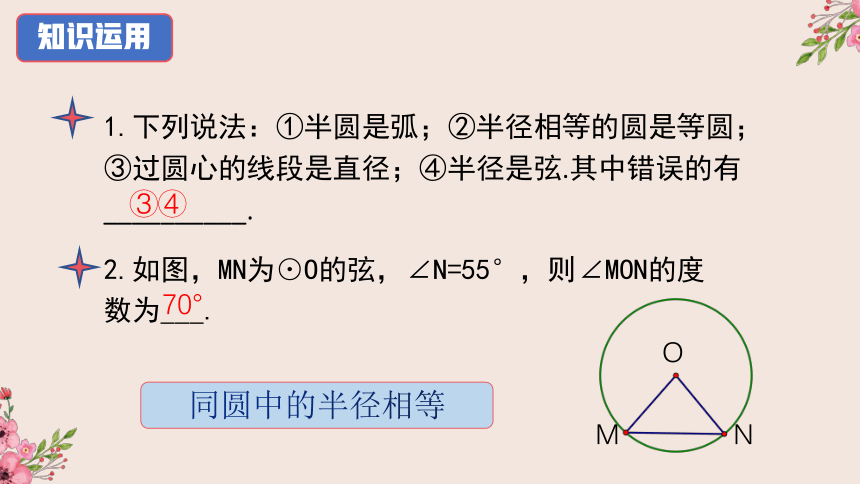
1.下列说法:①半圆是弧;②半径相等的圆是等圆;③过圆心的线段是直径;④半径是弦.其中错误的有__________.
2.如图,MN为⊙O的弦,∠N=55°,则∠MON的度数为___.
③④
70°
M
N
O
同圆中的半径相等
知识运用
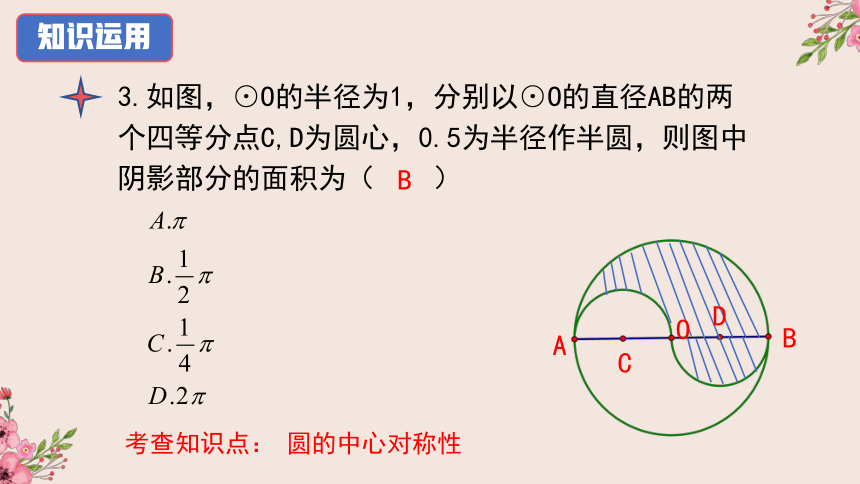
B
考查知识点:
圆的中心对称性
3.如图,⊙O的半径为1,分别以⊙O的直径AB的两个四等分点C,D为圆心,0.5为半径作半圆,则图中阴影部分的面积为(
)
A
D
C
O
B
知识回顾
二、三角形的外接圆
1.概念:经过三角形三个顶点的圆,叫做三角形的外接圆.
这个三角形是圆的内接三角形.
是三角形三条边中垂线的交点
2.外心:外接圆的圆心.
到三角形三个顶点的距离相等
一个三角形只有一个外接圆,一个圆有无数个内接三角形.
知识回顾
二、三角形的外接圆
3.三角形外心的位置
直角三角形的外接圆的半径等于斜边的一半.
锐角三角形的外心在三角形内.
直角三角形的外心在斜边中点.
钝角三角形的外心在三角形外.
知识运用
1.在Rt△ABC中,AB=3,BC=4,则△ABC的外接圆半径为_____.
考查知识点:
直角三角形的外接圆的半径等于斜边的一半.
注意之处:
题中没有指出直角,需分类讨论.
知识运用
2.若点A(1,2),点B(3,4)
(1)求直线AB的表达式.
(2)若点C(-1,6),则经过点A、B、C能否确定一个圆.
分析:
判断点A,B,C能否确定一个圆,需要判断这三个点是否在同一条直线上.
求出AB的表达式为y=x+1.把x=-1代入得,y=0≠6,因此点C不在直线AB上,则过点A,B,C能确定一个圆.
知识回顾
三、圆心角和圆周角
1.概念:
①圆心角:顶点在圆心的角.
②圆周角:顶点在圆上,并且两边都与圆相交的角.
③圆内接四边形:四个顶点都在同一个圆上的四边形.
知识回顾
三、圆心角和圆周角
1.结论:
②
同弧所对的圆周角等于圆心角的一半.
①在同圆或等圆中,两个圆心角及其所对应的两条弦和所对应的两条弧这三组量中,只要有一组量相等,其他两组量就分别相等.
④同弧或等弧所对的圆周角相等.
③直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
⑤圆内接四边形的对角互补.
知识运用
1.如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC=____.
注意:
1.已知中出现直径,常用的知识点:直径所对的圆周角是直角.
2.已知中出现特殊角度时,常用三角函数求边长.
A
O
D
C
B
知识运用
注意:
点A是动点,需考虑点A可以在在弦BC所对劣弧上,也可以在弦BC所对的优弧上.
2.如图,B,C是⊙O上两点,且∠α=80°,A是⊙O上一个动点(不与B,C重合),则∠BAC=__________.
40°或140°
O
A
B
C
α
●
知识回顾
四、垂径定理
1.垂径定理:垂直于弦的直径平分弦,并且平分
这条弦所对的两条弧.
用途:
①推出相等的角、线段、弧.
②求半径、弦或弦心距.
知识回顾
四、垂径定理
2.垂径定理的推论
①平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧.
②平分弧的直径垂直平分弧所对的弦.
知识运用
1.如图,AB为⊙O的直径,弦CD⊥AB于点D,已知CD=16,OE=6,则⊙O的直径为______.
分析:
A
O
D
C
B
E
连接OD
出现由半径、弦的一半、弦心距构成的直角三角形.
在直角三角形中,利用勾股定理求出半径.
20
知识运用
1.(变式)如图,AB为⊙O的直径,弦CD⊥AB于点D,已知CD=16,BE=6,则⊙O的直径为______.
分析:
A
O
D
C
B
E
连接OD
在直角三角形中,只知一条边长,可考虑用勾股方程解决问题.
设半径为x
则有(x-6)?+8?=x?.
知识回顾
五、弧长和扇形面积
1.弧长公式:
2.扇形面积:
知识回顾
五、弧长和扇形面积
3.圆锥的侧面积:
圆锥的母线
圆锥的底面周长
扇形的半径
扇形的弧长
A
O
P
B
知识运用
1.已知一个扇形的圆心角为150°,弧长是25π,求这个扇形的面积.
分析:
不管用哪一个公式都需要求出半径的长度.
扇形的两个面积公式
知识运用
2.若用一个半径为30cm,面积为300πcm?的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为_______.
分析:
10cm
综合练习
1.如图,AB是半圆O的直径,C,D是半圆O上的两点,且OD∥BC,OD与AC,角与点E.
(1)若∠B=70°,求∠CAD的度数.
综合练习
(2)若AB=4,AC=3,求DE的长.
综合练习
(1)求⊙O的半径.
2.如图,在⊙O中,半径OA⊥OB,过OA的中点C做FD∥OB交⊙O于D,F两点,且OD=
,以O为圆心,OC为半径做弧CE,交OB于E点.
综合练习
(2)计算阴影部分的面积.
同学们再见
复习与小结
冀教版九上
第二十八章
圆
学习目标
3.熟练运用弧长、扇形面积公式进行计算.
2.会用圆的有关性质,并掌握圆中常用的辅助线的作法.
1.熟记圆中的相关概念.
冀教版九上
知识回顾
一、圆的概念及性质
1.圆:
2.弦:
到定点的距离等于定长的所有点组成的图形.
确定圆的条件:圆心和半径.
圆上任意两点间的线段.
直径是圆中最长的弦.
知识回顾
一、圆的概念及性质
3.弧:
4.等圆:
圆上任意两点间的部分.
圆上的弧包括:优弧、半圆、劣弧.
能够完全重合的两个圆.
等弧只存在与同圆或等圆中.
5.等弧:
能够完全重合的两条弧.
知识回顾
一、圆的概念及性质
圆的对称性
1.圆是轴对称图形,对称轴是过圆心的直线,圆有无数条对称轴.
2.圆是中心对称图形,对称中心是圆心.
知识运用
1.下列说法:①半圆是弧;②半径相等的圆是等圆;③过圆心的线段是直径;④半径是弦.其中错误的有__________.
2.如图,MN为⊙O的弦,∠N=55°,则∠MON的度数为___.
③④
70°
M
N
O
同圆中的半径相等
知识运用
B
考查知识点:
圆的中心对称性
3.如图,⊙O的半径为1,分别以⊙O的直径AB的两个四等分点C,D为圆心,0.5为半径作半圆,则图中阴影部分的面积为(
)
A
D
C
O
B
知识回顾
二、三角形的外接圆
1.概念:经过三角形三个顶点的圆,叫做三角形的外接圆.
这个三角形是圆的内接三角形.
是三角形三条边中垂线的交点
2.外心:外接圆的圆心.
到三角形三个顶点的距离相等
一个三角形只有一个外接圆,一个圆有无数个内接三角形.
知识回顾
二、三角形的外接圆
3.三角形外心的位置
直角三角形的外接圆的半径等于斜边的一半.
锐角三角形的外心在三角形内.
直角三角形的外心在斜边中点.
钝角三角形的外心在三角形外.
知识运用
1.在Rt△ABC中,AB=3,BC=4,则△ABC的外接圆半径为_____.
考查知识点:
直角三角形的外接圆的半径等于斜边的一半.
注意之处:
题中没有指出直角,需分类讨论.
知识运用
2.若点A(1,2),点B(3,4)
(1)求直线AB的表达式.
(2)若点C(-1,6),则经过点A、B、C能否确定一个圆.
分析:
判断点A,B,C能否确定一个圆,需要判断这三个点是否在同一条直线上.
求出AB的表达式为y=x+1.把x=-1代入得,y=0≠6,因此点C不在直线AB上,则过点A,B,C能确定一个圆.
知识回顾
三、圆心角和圆周角
1.概念:
①圆心角:顶点在圆心的角.
②圆周角:顶点在圆上,并且两边都与圆相交的角.
③圆内接四边形:四个顶点都在同一个圆上的四边形.
知识回顾
三、圆心角和圆周角
1.结论:
②
同弧所对的圆周角等于圆心角的一半.
①在同圆或等圆中,两个圆心角及其所对应的两条弦和所对应的两条弧这三组量中,只要有一组量相等,其他两组量就分别相等.
④同弧或等弧所对的圆周角相等.
③直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
⑤圆内接四边形的对角互补.
知识运用
1.如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC=____.
注意:
1.已知中出现直径,常用的知识点:直径所对的圆周角是直角.
2.已知中出现特殊角度时,常用三角函数求边长.
A
O
D
C
B
知识运用
注意:
点A是动点,需考虑点A可以在在弦BC所对劣弧上,也可以在弦BC所对的优弧上.
2.如图,B,C是⊙O上两点,且∠α=80°,A是⊙O上一个动点(不与B,C重合),则∠BAC=__________.
40°或140°
O
A
B
C
α
●
知识回顾
四、垂径定理
1.垂径定理:垂直于弦的直径平分弦,并且平分
这条弦所对的两条弧.
用途:
①推出相等的角、线段、弧.
②求半径、弦或弦心距.
知识回顾
四、垂径定理
2.垂径定理的推论
①平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧.
②平分弧的直径垂直平分弧所对的弦.
知识运用
1.如图,AB为⊙O的直径,弦CD⊥AB于点D,已知CD=16,OE=6,则⊙O的直径为______.
分析:
A
O
D
C
B
E
连接OD
出现由半径、弦的一半、弦心距构成的直角三角形.
在直角三角形中,利用勾股定理求出半径.
20
知识运用
1.(变式)如图,AB为⊙O的直径,弦CD⊥AB于点D,已知CD=16,BE=6,则⊙O的直径为______.
分析:
A
O
D
C
B
E
连接OD
在直角三角形中,只知一条边长,可考虑用勾股方程解决问题.
设半径为x
则有(x-6)?+8?=x?.
知识回顾
五、弧长和扇形面积
1.弧长公式:
2.扇形面积:
知识回顾
五、弧长和扇形面积
3.圆锥的侧面积:
圆锥的母线
圆锥的底面周长
扇形的半径
扇形的弧长
A
O
P
B
知识运用
1.已知一个扇形的圆心角为150°,弧长是25π,求这个扇形的面积.
分析:
不管用哪一个公式都需要求出半径的长度.
扇形的两个面积公式
知识运用
2.若用一个半径为30cm,面积为300πcm?的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为_______.
分析:
10cm
综合练习
1.如图,AB是半圆O的直径,C,D是半圆O上的两点,且OD∥BC,OD与AC,角与点E.
(1)若∠B=70°,求∠CAD的度数.
综合练习
(2)若AB=4,AC=3,求DE的长.
综合练习
(1)求⊙O的半径.
2.如图,在⊙O中,半径OA⊥OB,过OA的中点C做FD∥OB交⊙O于D,F两点,且OD=
,以O为圆心,OC为半径做弧CE,交OB于E点.
综合练习
(2)计算阴影部分的面积.
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
