沪科版八年级上数学14.1全等三角形 课件(25张)
文档属性
| 名称 | 沪科版八年级上数学14.1全等三角形 课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 17:29:15 | ||
图片预览


文档简介
(共25张PPT)
14.1全等三角形
1、全等三角形的定义和表示
2、全等三角形的性质
3、全等三角形对应边、角的识别
4、应用举例
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
(5)
思考:他们能完全重合吗?
能够完全重合的两个图形叫做全等形
定义
:
你能举出现实生活中全等形的例子吗?
A
B
C
E
D
F
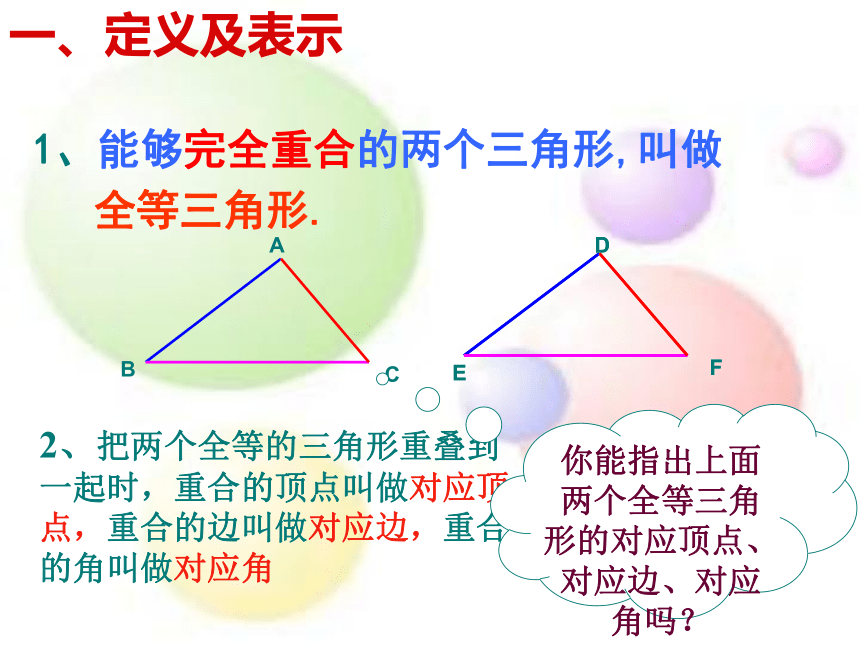
1、能够完全重合的两个三角形,叫做
全等三角形.
E
D
F
2、把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角
你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?
一、定义及表示
A
B
C
E
D
F
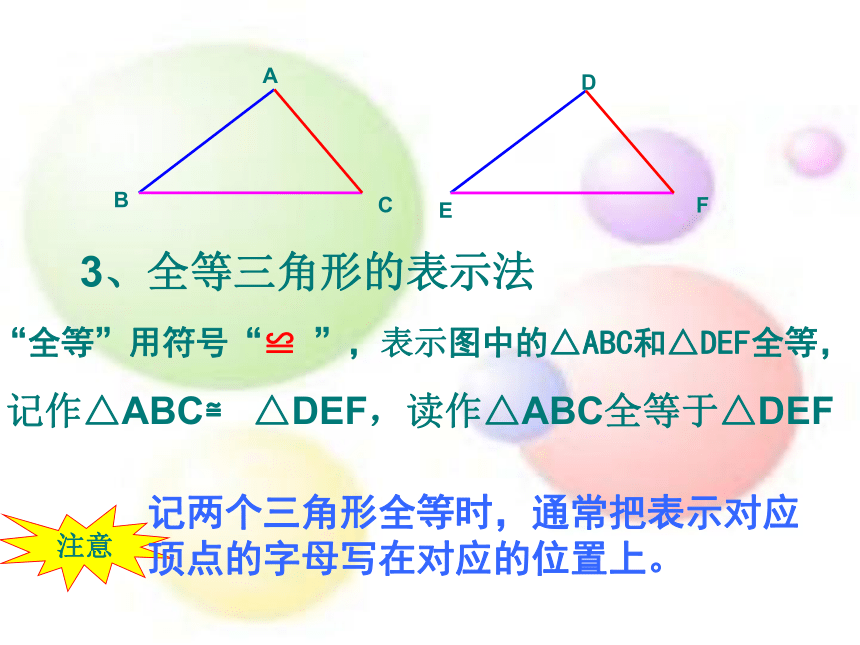
“全等”用符号“≌
”,表示图中的△ABC和△DEF全等,
3、全等三角形的表示法
记作△ABC≌
△DEF,读作△ABC全等于△DEF
注意
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
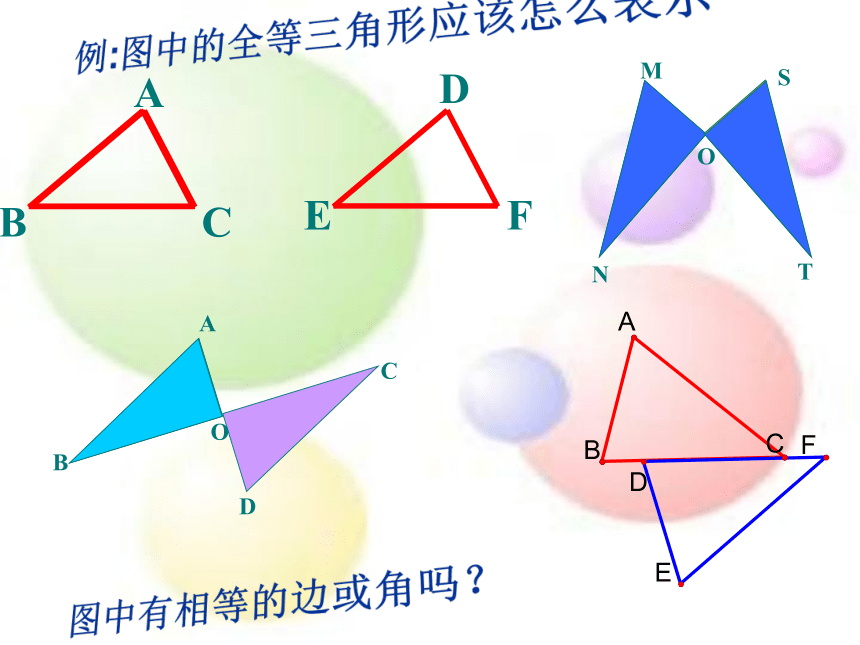
例:图中的全等三角形应该怎么表示
A
B
C
D
E
F
D
C
O
A
B
N
M
S
O
T
图中有相等的边或角吗?
三种语言
A
B
C
E
D
F
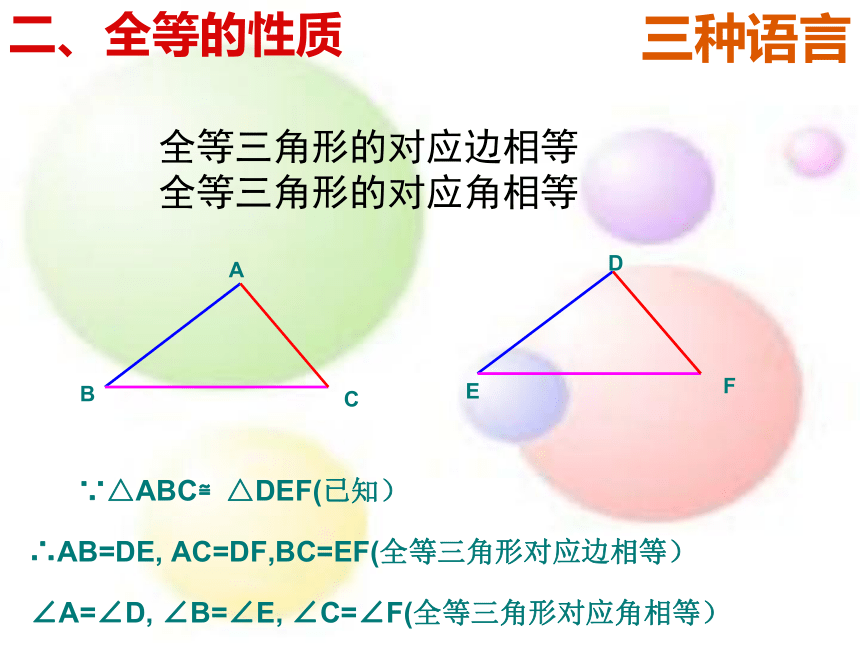
∵△ABC≌△DEF(已知)
∴AB=DE,
AC=DF,BC=EF(全等三角形对应边相等)
∠A=∠D,
∠B=∠E,
∠C=∠F(全等三角形对应角相等)
全等三角形的对应边相等
全等三角形的对应角相等
二、全等的性质
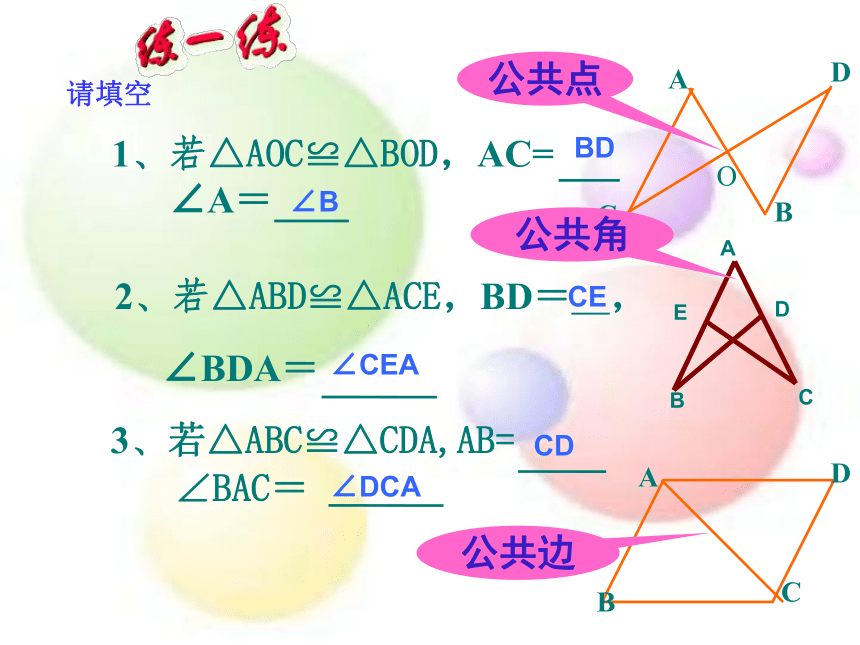
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA=
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
请填空
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
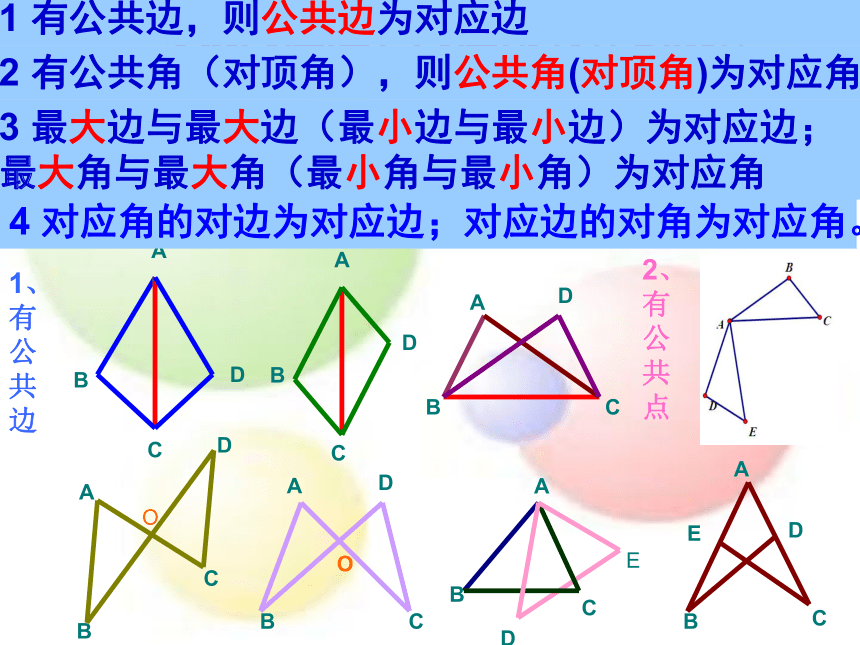
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
请你利用自制的一对全等三角形拼出有公共顶点或公共边或公共角的图形。试用全等符号表示它们,分析每个图形,找准对应边、对应角
寻找对应边、对应角有什么规律?
1
有公共边,则公共边为对应边
2
有公共角(对顶角),则公共角(对顶角)为对应角
3
最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角
4
对应角的对边为对应边;对应边的对角为对应角。
例1、已知:如图,△ABC
≌△
CED,
∠
B和∠
DEC是对应角,BC与ED是对应边,说出另两组对应角和对应边。
A
B
C
E
D
解:
对应角:
∠
A=
∠
DCE,
∠
D=
∠
ACB
对应边:
AC=CD,AB=CE
填一填
角
角
角
边
边
边
AB=DF
AC=DE
BC=EF
∠A=∠D
∠B=∠F
∠ACB=∠DEF
问题:
?ABC通过怎样的变化得到?DFE?
填一填
角
角
角
边
边
边
AC=BD
MC=MD
AM=BM
∠A=∠B
∠C=∠D
∠AMC=∠BMD
△___≌△___
AMC
BMD
1.请指出图中全等三角形的对应边和对应角
如右图中△
ABD
≌
△CDB,
则AB=
;AD=
;BD=
;
∠ABD=__
;
∠ADB=______
;
∠A=__
;
随堂练习
CD
CB
BD
∠CDB
∠CBD
∠C
AB与CD、AD与CB、BD与DB
∠ABD与∠CDB、
∠ADB与∠CBD、∠A与∠C
请指出下列全等三角形的对应边和对应角
1、
△
ABE
≌
△
ACF
对应角是:
∠A和∠A、
∠ABE和∠ACF、
∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。
2、
△
BCE
≌
△
CBF
对应角是:
∠BCE和
∠CBF、
∠BEC和∠CFB、
∠CBE和
∠BCF。对应边是:CB和BC、CE和BF、CF和BE。
3、
△
BOF
≌
△
COE
对应角是:
∠BOF和COE、
∠BFO
和∠CEO、
∠
FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。
右图是一个等边三角形,你能把它分成两个全等的三角形吗?你能把它分成三个、四个全等的三角形吗?
议一议
例2、已知:如图,△ABD≌△
ACE,
∠B=
∠
C,指出其他的对应角和对应边;
又知△
OBE≌△
OCD,指出这一对全等三角形中所有的对应角和对应边。
A
E
B
O
D
C
解
△ABD≌△ACE,
∠B=
∠C时
对应角:∠A=
∠A,
∠ADB=
∠AEC
对应边:AD=AE,CE=BD,AB=AC
回忆这节课,学习了全等三角形的哪些知识?
小结
1、全等三角形的定义和表示
2、全等三角形的性质
3、全等三角形对应边、角的识别
4、应用举例
达标测试
1、能够
的两个图形叫做全等形.
两个三角形重合时,互相
_的顶点
叫做对应顶点.记两个全等三角形时,
通常把表示
_顶点的字母写在____
的位置上.
A
B
C
D
E
2、如图△ABC≌
△ADE
若∠D=∠B,
∠C=
∠AED,
则∠DAE=
;
∠DAB=
。
重合
重合
重合
相对应
∠BAC
∠EAC
3、如图△
ABD
≌
△CDB,
若AB=4,AD=5,BD=6,则BC=
,CD=______,
达标测试
5
4
4、如图△ABD≌
△EBC,AB=3cm,BC=5cm,求DE的长
达标测试
解:
∵△ABD≌
△EBC
∴AB=EB、BD=BC
∵BD=DE+EB
∴DE=BD-EB
=BC-AB
=5-3=2cm
5.如图,矩形ABCD沿AM折叠,使D点落在BC上的N点处,如果AD=7cm,DM=5cm,
∠DAM=39°,则AN=___cm,
NM=___cm,
∠NAB=___.
M
D
A
N
B
C
7cm
5
cm
)39°
6.如图:已知△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠ACB=105?,∠CAD=10?,∠D=25?。
求
∠EAC,∠DFG,∠DGF的度数。
D
G
E
A
C
F
B
A
B
C
D
E
7.
如图所示,在△ABC中,D、E分别是边AC、BC上的点,若△EAB≌
△EDB≌
△EDC,则∠C的度数是(
)0
(A)15
(B)20
(C)25
(D)30
8.如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边,
∠BAC
与∠
EAD对应角,且∠BAC=25°,
∠B=35°,AB=3cm,BC=1cm,求出∠E,
∠
ADE的度数和线段DE,AE
的长度。
B
C
E
D
A
解:∵
△ABC≌△AED,(已知)
∴∠E=
∠B=
35°(全等三角形对应角相等)
∠ADE=∠ACB=18O°-
25°-
35°
=120
°
(全等三角形对应角相等)
DE=BC=1cm,
AE=AB=3cm
(全等三角形对应边相等)
如图,已知△
AOC
≌
△BOD
求证:AC∥BD
能力提高
14.1全等三角形
1、全等三角形的定义和表示
2、全等三角形的性质
3、全等三角形对应边、角的识别
4、应用举例
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
(5)
思考:他们能完全重合吗?
能够完全重合的两个图形叫做全等形
定义
:
你能举出现实生活中全等形的例子吗?
A
B
C
E
D
F
1、能够完全重合的两个三角形,叫做
全等三角形.
E
D
F
2、把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角
你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?
一、定义及表示
A
B
C
E
D
F
“全等”用符号“≌
”,表示图中的△ABC和△DEF全等,
3、全等三角形的表示法
记作△ABC≌
△DEF,读作△ABC全等于△DEF
注意
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
例:图中的全等三角形应该怎么表示
A
B
C
D
E
F
D
C
O
A
B
N
M
S
O
T
图中有相等的边或角吗?
三种语言
A
B
C
E
D
F
∵△ABC≌△DEF(已知)
∴AB=DE,
AC=DF,BC=EF(全等三角形对应边相等)
∠A=∠D,
∠B=∠E,
∠C=∠F(全等三角形对应角相等)
全等三角形的对应边相等
全等三角形的对应角相等
二、全等的性质
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA=
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
请填空
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
请你利用自制的一对全等三角形拼出有公共顶点或公共边或公共角的图形。试用全等符号表示它们,分析每个图形,找准对应边、对应角
寻找对应边、对应角有什么规律?
1
有公共边,则公共边为对应边
2
有公共角(对顶角),则公共角(对顶角)为对应角
3
最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角
4
对应角的对边为对应边;对应边的对角为对应角。
例1、已知:如图,△ABC
≌△
CED,
∠
B和∠
DEC是对应角,BC与ED是对应边,说出另两组对应角和对应边。
A
B
C
E
D
解:
对应角:
∠
A=
∠
DCE,
∠
D=
∠
ACB
对应边:
AC=CD,AB=CE
填一填
角
角
角
边
边
边
AB=DF
AC=DE
BC=EF
∠A=∠D
∠B=∠F
∠ACB=∠DEF
问题:
?ABC通过怎样的变化得到?DFE?
填一填
角
角
角
边
边
边
AC=BD
MC=MD
AM=BM
∠A=∠B
∠C=∠D
∠AMC=∠BMD
△___≌△___
AMC
BMD
1.请指出图中全等三角形的对应边和对应角
如右图中△
ABD
≌
△CDB,
则AB=
;AD=
;BD=
;
∠ABD=__
;
∠ADB=______
;
∠A=__
;
随堂练习
CD
CB
BD
∠CDB
∠CBD
∠C
AB与CD、AD与CB、BD与DB
∠ABD与∠CDB、
∠ADB与∠CBD、∠A与∠C
请指出下列全等三角形的对应边和对应角
1、
△
ABE
≌
△
ACF
对应角是:
∠A和∠A、
∠ABE和∠ACF、
∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。
2、
△
BCE
≌
△
CBF
对应角是:
∠BCE和
∠CBF、
∠BEC和∠CFB、
∠CBE和
∠BCF。对应边是:CB和BC、CE和BF、CF和BE。
3、
△
BOF
≌
△
COE
对应角是:
∠BOF和COE、
∠BFO
和∠CEO、
∠
FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。
右图是一个等边三角形,你能把它分成两个全等的三角形吗?你能把它分成三个、四个全等的三角形吗?
议一议
例2、已知:如图,△ABD≌△
ACE,
∠B=
∠
C,指出其他的对应角和对应边;
又知△
OBE≌△
OCD,指出这一对全等三角形中所有的对应角和对应边。
A
E
B
O
D
C
解
△ABD≌△ACE,
∠B=
∠C时
对应角:∠A=
∠A,
∠ADB=
∠AEC
对应边:AD=AE,CE=BD,AB=AC
回忆这节课,学习了全等三角形的哪些知识?
小结
1、全等三角形的定义和表示
2、全等三角形的性质
3、全等三角形对应边、角的识别
4、应用举例
达标测试
1、能够
的两个图形叫做全等形.
两个三角形重合时,互相
_的顶点
叫做对应顶点.记两个全等三角形时,
通常把表示
_顶点的字母写在____
的位置上.
A
B
C
D
E
2、如图△ABC≌
△ADE
若∠D=∠B,
∠C=
∠AED,
则∠DAE=
;
∠DAB=
。
重合
重合
重合
相对应
∠BAC
∠EAC
3、如图△
ABD
≌
△CDB,
若AB=4,AD=5,BD=6,则BC=
,CD=______,
达标测试
5
4
4、如图△ABD≌
△EBC,AB=3cm,BC=5cm,求DE的长
达标测试
解:
∵△ABD≌
△EBC
∴AB=EB、BD=BC
∵BD=DE+EB
∴DE=BD-EB
=BC-AB
=5-3=2cm
5.如图,矩形ABCD沿AM折叠,使D点落在BC上的N点处,如果AD=7cm,DM=5cm,
∠DAM=39°,则AN=___cm,
NM=___cm,
∠NAB=___.
M
D
A
N
B
C
7cm
5
cm
)39°
6.如图:已知△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠ACB=105?,∠CAD=10?,∠D=25?。
求
∠EAC,∠DFG,∠DGF的度数。
D
G
E
A
C
F
B
A
B
C
D
E
7.
如图所示,在△ABC中,D、E分别是边AC、BC上的点,若△EAB≌
△EDB≌
△EDC,则∠C的度数是(
)0
(A)15
(B)20
(C)25
(D)30
8.如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边,
∠BAC
与∠
EAD对应角,且∠BAC=25°,
∠B=35°,AB=3cm,BC=1cm,求出∠E,
∠
ADE的度数和线段DE,AE
的长度。
B
C
E
D
A
解:∵
△ABC≌△AED,(已知)
∴∠E=
∠B=
35°(全等三角形对应角相等)
∠ADE=∠ACB=18O°-
25°-
35°
=120
°
(全等三角形对应角相等)
DE=BC=1cm,
AE=AB=3cm
(全等三角形对应边相等)
如图,已知△
AOC
≌
△BOD
求证:AC∥BD
能力提高
