人教版八年级数学上册 14.1.4 同底数幂相除 课件(17张)
文档属性
| 名称 | 人教版八年级数学上册 14.1.4 同底数幂相除 课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 17:32:51 | ||
图片预览



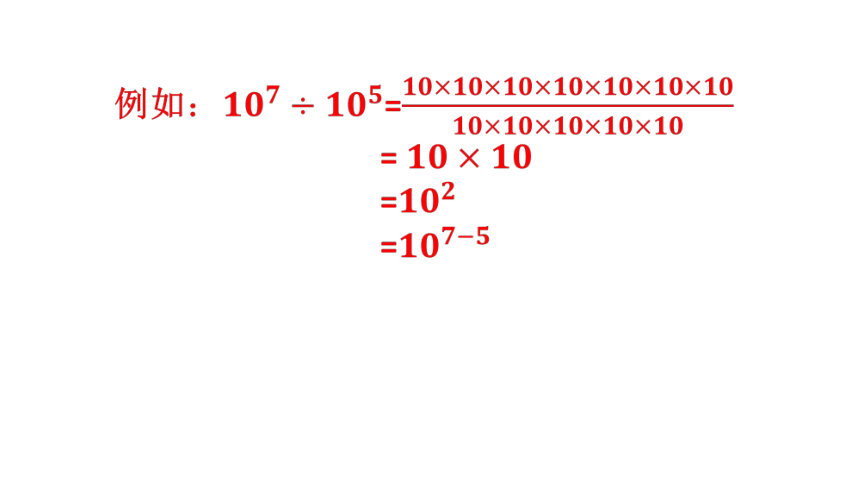

文档简介
(共17张PPT)
中物理
第十四章
整式的乘法与因式分解
14.1.4
同底数幂相除
前言
学习目标
重点
同底数幂的除法的运算性质和零指数幂的意义。
难点
同底数幂的除法的运算中指数的运算。
1、理解同底数幂的除法法则,会进行同底数幂的除法的运算。
2、懂得零指数幂的意义,并会进行相关运算。
3、探索单项式除以单项式及多项式除以单项式运算法则。
复习反馈:
1.同底数幂的乘法公式是什么?怎样用语言描述?
am×an=am+n
(m,n为正整数)
2.推导过程是怎样的?
am×an=
=a×a×.....×a
m+n个a
=am+n
a×a×a×...×a
m个a
×a×a×.....×a
n个a
计算:
(1)(
)·28=216
(2)(
)·53=55
(3)(
)·105=107
(4)(
)·a3=a6
28
52
102
a3
计算:
(1)216÷28=(
)
(2)55÷53=(
)
(3)107÷105=(
)(4)a6÷a3=(
)
28
52
102
a3
通过运算能否发现商与除数、被除数有什么关系?
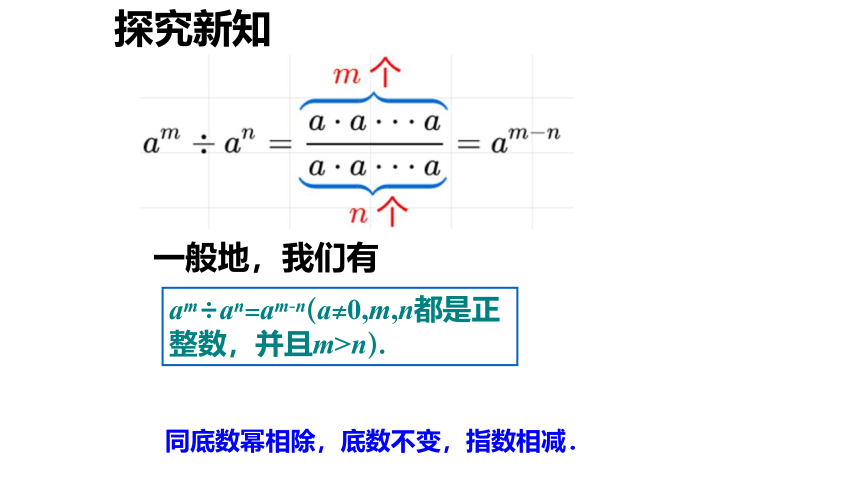
探究新知
?
探究新知
同底数幂相除,底数不变,指数相减.
一般地,我们有
am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
同底数幂的注意事项
1.因为0不能做除数,所以底数a≠0.
2.运用同底数幂法则关键看底数是否相同,而指数相减是指被除式的指数减去除式的指数。
3.注意指数为1的情况,如x8÷x=
x7
,计算时候容易遗漏或将x的指数当做0.
4.多个同底数幂相除时,应按顺序计算。
练习1 下面的计算对不对?若不对,应当怎样改
正?
(1)
(2)
(3)
(4)
不对,改正:a3÷a=a2.
不对,改正:x6÷x2=x4.
对.
不对,改正:(-c)4÷(-c)2=(-c)2=c2.
例题
例1
计算:
(1)x8÷x2
;
(2)
a4
÷a
;
(3)(ab)
5÷(ab)2;
(4)(-a)7÷(-a)5
(5)
(-b)
5÷(-b)2
(5)(-b)5÷(-b)2=(-b)5-2=(-b)3=-b3
解:
(1)
x8
÷x2=x
8-2=x6.
(2)a4
÷a
=a
4-1=a3.
(3)
(ab)
5÷(ab)2=(ab)5-2=(ab)3
=a3b3.
(4)(-a)7÷(-a)5=(-a)7-5=(-a)2=a2
注意结果算到底!
(1)
a9÷a3
(2)
212÷27
=a9-3
=a6.
=212-7=25=32.
(3)
(-x)4÷(-x)
=(-x)4-1=(-x)3=
-x3.
(4)
(-3)11÷(-3)8
=(-3)11-8=(-3)3=-27.
1、计算:
随堂练习
探究新知
猜想:根据除法的意义计算,你能得到什么结论?
?
?
?
1
1
1
?
?
?
?
例2:计算下列各式:
(1)
13690
(2)
(700-42×32)0
(3)
a5÷(a0)8
(4)
(an)0·a2+n÷a3
=1
=1
=
a5
=1
·
a2+n
÷
a3
=
an-1
=a5
÷
1
实践与创新
思维延伸
已知:xa=4,xb=9,求(1)x
a-b;(2)x
3a-2b
am÷an=am-n,
则am-n=am÷an
这种思维叫做逆向思维!
解:
当xa=4,xb=9时,
(1)xa-b=xa÷xb=4÷9=
(2)x3a-2b=x3a÷x2b=(xa)3÷(xb)2
=43÷92=
已学过的幂运算性质:
(1)am·an=
(a≠0
m、n为正整数)
(2)am÷an=
(a≠0
m、n为正整数且m>n)
(3)(am)n=
(a≠0
m、n为正整数)
(4)(ab)n=
(a≠0
m、n为正整数)
(5)a0=
(a≠0)
归纳与梳理
am+n
am-n
amn
anbn
1
课堂小结:
?
1.同底数幂除法
2.零指数幂
?
课堂检测
?
?
3
?
如果x2m-1
÷
x2
=xm+1,求m的值.
解:∵
x2m-1
÷
x2
=xm+1
,
∴2m-1-2=m+1,
解得:m=4.
中物理
第十四章
整式的乘法与因式分解
14.1.4
同底数幂相除
前言
学习目标
重点
同底数幂的除法的运算性质和零指数幂的意义。
难点
同底数幂的除法的运算中指数的运算。
1、理解同底数幂的除法法则,会进行同底数幂的除法的运算。
2、懂得零指数幂的意义,并会进行相关运算。
3、探索单项式除以单项式及多项式除以单项式运算法则。
复习反馈:
1.同底数幂的乘法公式是什么?怎样用语言描述?
am×an=am+n
(m,n为正整数)
2.推导过程是怎样的?
am×an=
=a×a×.....×a
m+n个a
=am+n
a×a×a×...×a
m个a
×a×a×.....×a
n个a
计算:
(1)(
)·28=216
(2)(
)·53=55
(3)(
)·105=107
(4)(
)·a3=a6
28
52
102
a3
计算:
(1)216÷28=(
)
(2)55÷53=(
)
(3)107÷105=(
)(4)a6÷a3=(
)
28
52
102
a3
通过运算能否发现商与除数、被除数有什么关系?
探究新知
?
探究新知
同底数幂相除,底数不变,指数相减.
一般地,我们有
am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
同底数幂的注意事项
1.因为0不能做除数,所以底数a≠0.
2.运用同底数幂法则关键看底数是否相同,而指数相减是指被除式的指数减去除式的指数。
3.注意指数为1的情况,如x8÷x=
x7
,计算时候容易遗漏或将x的指数当做0.
4.多个同底数幂相除时,应按顺序计算。
练习1 下面的计算对不对?若不对,应当怎样改
正?
(1)
(2)
(3)
(4)
不对,改正:a3÷a=a2.
不对,改正:x6÷x2=x4.
对.
不对,改正:(-c)4÷(-c)2=(-c)2=c2.
例题
例1
计算:
(1)x8÷x2
;
(2)
a4
÷a
;
(3)(ab)
5÷(ab)2;
(4)(-a)7÷(-a)5
(5)
(-b)
5÷(-b)2
(5)(-b)5÷(-b)2=(-b)5-2=(-b)3=-b3
解:
(1)
x8
÷x2=x
8-2=x6.
(2)a4
÷a
=a
4-1=a3.
(3)
(ab)
5÷(ab)2=(ab)5-2=(ab)3
=a3b3.
(4)(-a)7÷(-a)5=(-a)7-5=(-a)2=a2
注意结果算到底!
(1)
a9÷a3
(2)
212÷27
=a9-3
=a6.
=212-7=25=32.
(3)
(-x)4÷(-x)
=(-x)4-1=(-x)3=
-x3.
(4)
(-3)11÷(-3)8
=(-3)11-8=(-3)3=-27.
1、计算:
随堂练习
探究新知
猜想:根据除法的意义计算,你能得到什么结论?
?
?
?
1
1
1
?
?
?
?
例2:计算下列各式:
(1)
13690
(2)
(700-42×32)0
(3)
a5÷(a0)8
(4)
(an)0·a2+n÷a3
=1
=1
=
a5
=1
·
a2+n
÷
a3
=
an-1
=a5
÷
1
实践与创新
思维延伸
已知:xa=4,xb=9,求(1)x
a-b;(2)x
3a-2b
am÷an=am-n,
则am-n=am÷an
这种思维叫做逆向思维!
解:
当xa=4,xb=9时,
(1)xa-b=xa÷xb=4÷9=
(2)x3a-2b=x3a÷x2b=(xa)3÷(xb)2
=43÷92=
已学过的幂运算性质:
(1)am·an=
(a≠0
m、n为正整数)
(2)am÷an=
(a≠0
m、n为正整数且m>n)
(3)(am)n=
(a≠0
m、n为正整数)
(4)(ab)n=
(a≠0
m、n为正整数)
(5)a0=
(a≠0)
归纳与梳理
am+n
am-n
amn
anbn
1
课堂小结:
?
1.同底数幂除法
2.零指数幂
?
课堂检测
?
?
3
?
如果x2m-1
÷
x2
=xm+1,求m的值.
解:∵
x2m-1
÷
x2
=xm+1
,
∴2m-1-2=m+1,
解得:m=4.
