人教版八年级数学上册教学课件:14.1.1 同底数幂的乘法(16张)
文档属性
| 名称 | 人教版八年级数学上册教学课件:14.1.1 同底数幂的乘法(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 680.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
14.1.1
同底数幂的乘法
整式的乘法
人教版八年级上册
2.
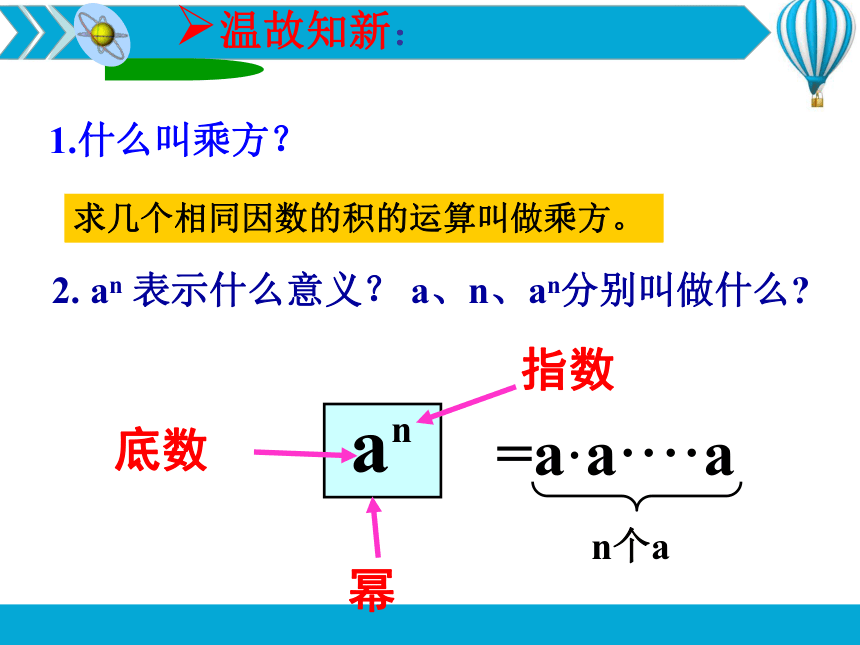
an
表示什么意义?
a、n、an分别叫做什么?
温故知新:
a
n
指数
幂
底数
=a·a····a
n个a
1.什么叫乘方?
求几个相同因数的积的运算叫做乘方。
试试你还会吗?
①
25
=
.
②
10×10×10×10×10
=
.
③
(-2)3底数是
指数是
表示
结果是
。
④(-2)4
底数是
指数是
结果是
。
(乘方的意义)
2×2×2×2×2
105
(乘方的意义)
-2
3
(-2)
×(-2)
×(-2)
4
16
-8
-2
(1)25×22
=
(
)
×(
)
=
=2(
)
;
(2)a3
·
a2
=
(
)
×
(
)
=____________
=
a(
)
;
(3)
5m
·
5n
=(
)
×(
)
2
×
2
×2×2×
2
2
×
2
2×2
×2
×
2×2×2×2
7
a
·
a
·
a
a
·
a
a
·
a
·
a
·
a
·
a
5
m+n
请同学们根据乘方的意义理解,完成下列填空.
5×···×5
m个5
n个5
5×···×5
探究新知
=(
)
=
5(
).
(m+n)个5
5×5×
···×5
×5
25
×22
=
2
a
×a
=
a
5m×
5n
=
5
3
5
m+n
猜想:
am
·
an=
?
(m、n都是正整数)
归纳算法:
请同学们观察:
上面三个同底数幂的乘法算式:
你发现了什么规律?
2
7
验证:
am
·
an=
(当m、n都是正整数)
am+n
am
·
an
=
(aa…a)
m个a
(aa…a)
n个a
(乘方的意义)
=
aa…a
(m+n)个a
(乘法结合律)
=am+n
(乘方的意义)
即
am
·
an
=
am+n
(当m、n都是正整数)
同底数幂的乘法:
am
·
an
=
am+n
(当m、n都是正整数)
那么你能用文字概括一下这个结论吗?
法则:同底数幂相乘,
底数 ,指数 。
不变
相加
运算形式
运算方法
(同底、乘法)
(底不变、指加法)
公式:
想一想:
当三个或三个以上同底数幂相乘时,是否也
具有这一性质呢?
怎样用公式表示?
如
am·an·ap
=
am+n+p
(m、n、p都是正整数)
小试牛刀(口答)
(1)
105×106
=
(2)
a7
·a3
=
(3)
(-2)2×23
=
1011
a10
(4
)(a+b)2
·
=
(a+b)7
(5
)
×3m
=
32+m
(6
)-x2
·x3
·
=
-x7
(a+b)5
32
x2
25
下面的计算对不对?如果不对,怎样改正?
(1)b5
·
b5=
2b5
(
)
(2)b5
+
b5
=
b10
(
)
(3)x5
·x5
=
x25
(
)
(4)y5
·
y5
=
2y10
(
)
(5)c
·
c3
=
c3
(
)
(6)m
+
m3
=
m4
(
)
×
×
×
×
×
×
火眼金睛
例1
计算:
(1)
-a
·
a6
;
(2)
xm
·
x3m+1
;
巩固法则
①单个字母或数字的指数为1;
②底数为负数时要加括号;
注意:
(4)
3x
·
x
-
x3
·
x2
4
(3)-a3·(-a)4·(-a)5
③若底数不相同,应先化相同.
思维拓展
计算:
思考:
把
化为同底数幂,应该怎样变形?
温馨提示:
1.同底数幂相乘时,指数是相加的;
2.底数为负数时,先用同底数幂的乘法法则计算,最后确定结果的正负;并且化简到底
3.不能疏忽指数为1的情况;
4.公式中的a可为一个有理数、单项式或多项式(整体思想)
5.如果底数互为相反数时可先变成同底后再运算
已知
=4,
=3,求
的值。
a
m
a
n
a
m+n
解:
a
m+n
=4×3=12
a
n
?
a
m
=
am+n=am
?an
例3
点拨:同底数幂乘法公式的逆用也很重要.
am
·
an
=am+n(m,n都是正整数).
同底数幂的乘法公式:
本节课,你有哪些收获?
am·
an·
ap
=
am+n+p
(m、n、p都是正整数).
回顾小结
.
(逆运算)
am+n
=
am
·
an
(m、n为正整数)
从特殊到一般和从一般到特殊的重要思想。
布置作业
1.教科书96页练习(2)(4)
2.习题14.1第1(1)(2)题
智慧往往隐藏在一个人每时每刻的思索和学习中。相信有付出就会有收获,加油同学们,你们是最棒的!
寄
语
14.1.1
同底数幂的乘法
整式的乘法
人教版八年级上册
2.
an
表示什么意义?
a、n、an分别叫做什么?
温故知新:
a
n
指数
幂
底数
=a·a····a
n个a
1.什么叫乘方?
求几个相同因数的积的运算叫做乘方。
试试你还会吗?
①
25
=
.
②
10×10×10×10×10
=
.
③
(-2)3底数是
指数是
表示
结果是
。
④(-2)4
底数是
指数是
结果是
。
(乘方的意义)
2×2×2×2×2
105
(乘方的意义)
-2
3
(-2)
×(-2)
×(-2)
4
16
-8
-2
(1)25×22
=
(
)
×(
)
=
=2(
)
;
(2)a3
·
a2
=
(
)
×
(
)
=____________
=
a(
)
;
(3)
5m
·
5n
=(
)
×(
)
2
×
2
×2×2×
2
2
×
2
2×2
×2
×
2×2×2×2
7
a
·
a
·
a
a
·
a
a
·
a
·
a
·
a
·
a
5
m+n
请同学们根据乘方的意义理解,完成下列填空.
5×···×5
m个5
n个5
5×···×5
探究新知
=(
)
=
5(
).
(m+n)个5
5×5×
···×5
×5
25
×22
=
2
a
×a
=
a
5m×
5n
=
5
3
5
m+n
猜想:
am
·
an=
?
(m、n都是正整数)
归纳算法:
请同学们观察:
上面三个同底数幂的乘法算式:
你发现了什么规律?
2
7
验证:
am
·
an=
(当m、n都是正整数)
am+n
am
·
an
=
(aa…a)
m个a
(aa…a)
n个a
(乘方的意义)
=
aa…a
(m+n)个a
(乘法结合律)
=am+n
(乘方的意义)
即
am
·
an
=
am+n
(当m、n都是正整数)
同底数幂的乘法:
am
·
an
=
am+n
(当m、n都是正整数)
那么你能用文字概括一下这个结论吗?
法则:同底数幂相乘,
底数 ,指数 。
不变
相加
运算形式
运算方法
(同底、乘法)
(底不变、指加法)
公式:
想一想:
当三个或三个以上同底数幂相乘时,是否也
具有这一性质呢?
怎样用公式表示?
如
am·an·ap
=
am+n+p
(m、n、p都是正整数)
小试牛刀(口答)
(1)
105×106
=
(2)
a7
·a3
=
(3)
(-2)2×23
=
1011
a10
(4
)(a+b)2
·
=
(a+b)7
(5
)
×3m
=
32+m
(6
)-x2
·x3
·
=
-x7
(a+b)5
32
x2
25
下面的计算对不对?如果不对,怎样改正?
(1)b5
·
b5=
2b5
(
)
(2)b5
+
b5
=
b10
(
)
(3)x5
·x5
=
x25
(
)
(4)y5
·
y5
=
2y10
(
)
(5)c
·
c3
=
c3
(
)
(6)m
+
m3
=
m4
(
)
×
×
×
×
×
×
火眼金睛
例1
计算:
(1)
-a
·
a6
;
(2)
xm
·
x3m+1
;
巩固法则
①单个字母或数字的指数为1;
②底数为负数时要加括号;
注意:
(4)
3x
·
x
-
x3
·
x2
4
(3)-a3·(-a)4·(-a)5
③若底数不相同,应先化相同.
思维拓展
计算:
思考:
把
化为同底数幂,应该怎样变形?
温馨提示:
1.同底数幂相乘时,指数是相加的;
2.底数为负数时,先用同底数幂的乘法法则计算,最后确定结果的正负;并且化简到底
3.不能疏忽指数为1的情况;
4.公式中的a可为一个有理数、单项式或多项式(整体思想)
5.如果底数互为相反数时可先变成同底后再运算
已知
=4,
=3,求
的值。
a
m
a
n
a
m+n
解:
a
m+n
=4×3=12
a
n
?
a
m
=
am+n=am
?an
例3
点拨:同底数幂乘法公式的逆用也很重要.
am
·
an
=am+n(m,n都是正整数).
同底数幂的乘法公式:
本节课,你有哪些收获?
am·
an·
ap
=
am+n+p
(m、n、p都是正整数).
回顾小结
.
(逆运算)
am+n
=
am
·
an
(m、n为正整数)
从特殊到一般和从一般到特殊的重要思想。
布置作业
1.教科书96页练习(2)(4)
2.习题14.1第1(1)(2)题
智慧往往隐藏在一个人每时每刻的思索和学习中。相信有付出就会有收获,加油同学们,你们是最棒的!
寄
语
