人教版七年级数学上册教学课件-3.4 实际问题与一元一次方程(18张)
文档属性
| 名称 | 人教版七年级数学上册教学课件-3.4 实际问题与一元一次方程(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 17:52:24 | ||
图片预览





文档简介
(共18张PPT)
课题:3.4
实际问题与一元一次方程等积变形问题
人教版七年级-上册-第三章
难点名称:等积变形的等量关系
学习目标
1.正确分析等积变形问题中的数量关系,利用一元一次方程解决问题.
2.掌握用一元一次方程解决问题的基本过程.
等积变形问题
◆周长的变形
◆面积的变形
◆体积的变形
等长变形
12米铁丝
变形前的长度=变形后的周长.
长方形
1、小明想用一根长为12米的铁丝围成一个长方形
哪些量发生了变化?哪些量保持不变?
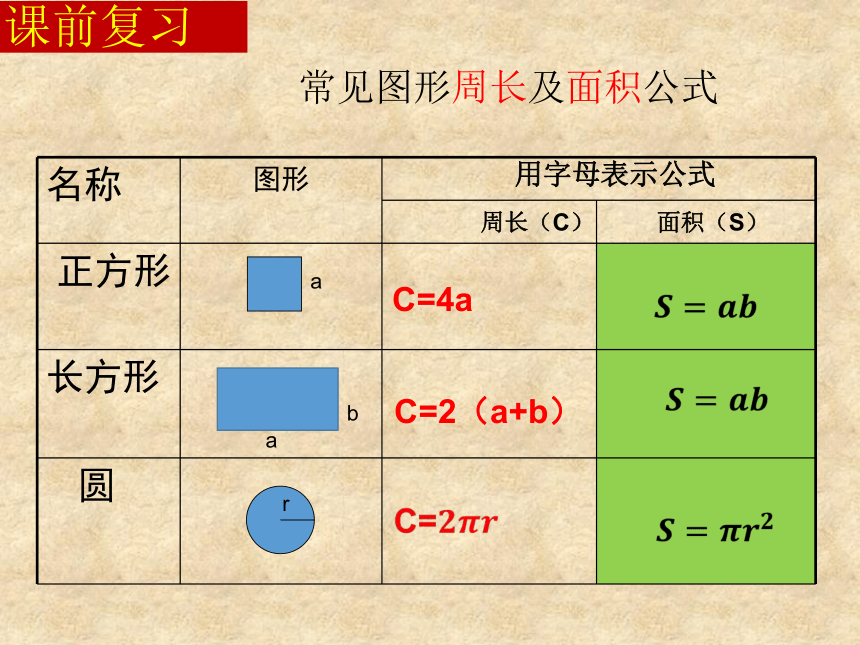
常见图形周长及面积公式
名称
图形
正方形
长方形
圆
a
用字母表示公式
周长(C)
面积(S)
课前复习
r
a
b
C=4a
C=2(a+b)
?
?
?
?
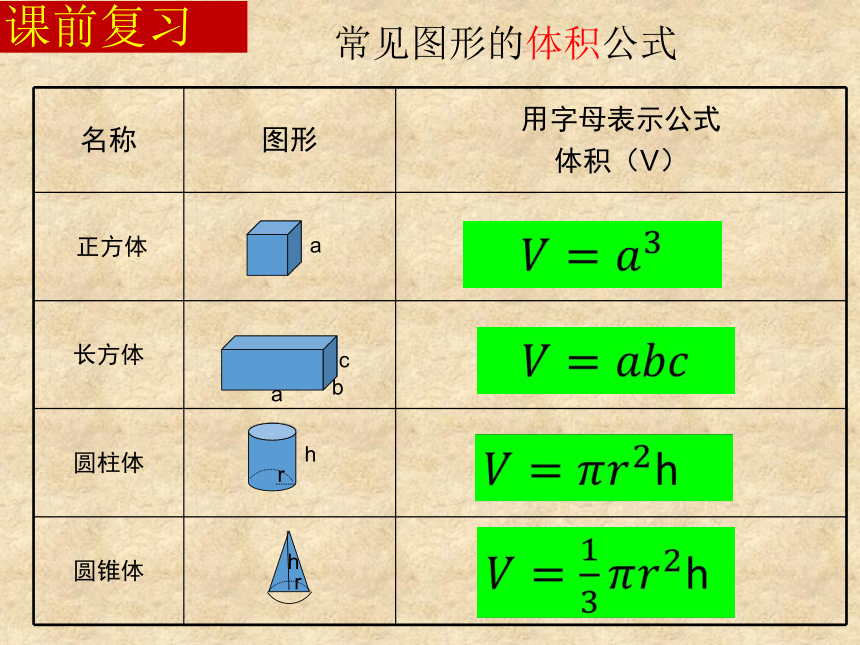
常见图形的体积公式
名称
图形
用字母表示公式
体积(V)
正方体
长方体
圆柱体
圆锥体
a
a
b
c
r
h
r
h
课前复习
?
?
?
?
小明想用一根长为12米的铁丝围成一个长方形.
(1)使得这个长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?
例题讲解(1)
解:设此时长方形的宽为x米,
2(x+x+1.4)=12
4x=9.2
x=2.3
长方形的长为2.3+1.4=3.7
∴长方形的长为3.7米,宽为2.3米
则它的长为(x+1.4)米,
根据题意,得
长=宽+1.4
2(长+宽)=12
(2)使得长方形的长比宽多一倍,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围成的长方形相比、面积有什么变化?
解:设此时长方形的宽为x米,
2(x+2x)=12
x=2
长方形的长2x
=4
则它的长为2x米,
根据题意,得
∴长方形的长为4米,宽为2米,
S=4×2=8米2,
(1)中的长方形围成的面积:3.7×2.3=8.51米2
比(1)中面积减少了8.51-8=0.51米2
2x
例题讲解(2)
小明想用一根长为12米的铁丝围成一个长方形.
周长相等的长方形面积不定
长=宽+宽
2(长+宽)=12
(3)使得围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中相比又有什么变化?
解:设此时正方形的边长为x米,根据题意,得
4x=12
x=3
比(2)中面积增大8-8=1
米2
X
正方形的边长为3米,
S=3×3=9米2
同样长的铁丝围成怎样的四边形面积最大呢?
例题讲解(3)
小明想用一根长为12米的铁丝围成一个长方形.
长=宽
?
面积:
3.7×2.3=
8.51
面积:
2
×4=8
面积:
3
×3=9
围成正方形时四边形面积最大
小结
(4)在墙边围成一个菜地,使长比宽大4米,问小明围成的菜地的长和宽各是多少呢?(墙面足够长)
例题讲解(4)
小明想用一根长为12米的铁丝围成一个长方形.
铁丝
墙面
x
x+4
解:设此时长方形的宽为x米,
2(2x+x+4)=12
则它的长为(x+4)米,
根据题意,得
长=宽+4
2宽+长=12
用一元一次方程解决实际问题的基本过程和步骤:
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x
=
a)
实际问题的答案
检
验
关键:找出等量关系,将实际问题抽象为方程这一数学模型
归纳总结
审
设
列
解
答
验
等体积变形
?
200
x
80
300
30
200
x
80
300
300
分
析
1:等量关系
2:用字母(未知数x)表示圆钢和长方体的体积
3:根据等量关系列出方程
4:解方程
锻造前圆柱的体积=锻造后长方体的体积
?
?
?
解:设截取圆钢的长度为x厘米,则填写下表
圆柱体
长方体
底面积
高(长)
体积
?
?
?
?
?
?
200
x
80
300
30
解:设截取圆钢的长度为x厘米,则由题意得
?
化简得:3.14x=720,
x≈230。
答:设截取圆钢的长度为230厘米,
1、等积变形问题的等量关系
变形前的体积(周长)=变形后的体积(周长)
小结
2、用方程解决实际问题的基本过程和步骤
再见
人生变幻莫测,但有不变的规则
事件一成不变,却有可变的态度
课题:3.4
实际问题与一元一次方程等积变形问题
人教版七年级-上册-第三章
难点名称:等积变形的等量关系
学习目标
1.正确分析等积变形问题中的数量关系,利用一元一次方程解决问题.
2.掌握用一元一次方程解决问题的基本过程.
等积变形问题
◆周长的变形
◆面积的变形
◆体积的变形
等长变形
12米铁丝
变形前的长度=变形后的周长.
长方形
1、小明想用一根长为12米的铁丝围成一个长方形
哪些量发生了变化?哪些量保持不变?
常见图形周长及面积公式
名称
图形
正方形
长方形
圆
a
用字母表示公式
周长(C)
面积(S)
课前复习
r
a
b
C=4a
C=2(a+b)
?
?
?
?
常见图形的体积公式
名称
图形
用字母表示公式
体积(V)
正方体
长方体
圆柱体
圆锥体
a
a
b
c
r
h
r
h
课前复习
?
?
?
?
小明想用一根长为12米的铁丝围成一个长方形.
(1)使得这个长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?
例题讲解(1)
解:设此时长方形的宽为x米,
2(x+x+1.4)=12
4x=9.2
x=2.3
长方形的长为2.3+1.4=3.7
∴长方形的长为3.7米,宽为2.3米
则它的长为(x+1.4)米,
根据题意,得
长=宽+1.4
2(长+宽)=12
(2)使得长方形的长比宽多一倍,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围成的长方形相比、面积有什么变化?
解:设此时长方形的宽为x米,
2(x+2x)=12
x=2
长方形的长2x
=4
则它的长为2x米,
根据题意,得
∴长方形的长为4米,宽为2米,
S=4×2=8米2,
(1)中的长方形围成的面积:3.7×2.3=8.51米2
比(1)中面积减少了8.51-8=0.51米2
2x
例题讲解(2)
小明想用一根长为12米的铁丝围成一个长方形.
周长相等的长方形面积不定
长=宽+宽
2(长+宽)=12
(3)使得围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中相比又有什么变化?
解:设此时正方形的边长为x米,根据题意,得
4x=12
x=3
比(2)中面积增大8-8=1
米2
X
正方形的边长为3米,
S=3×3=9米2
同样长的铁丝围成怎样的四边形面积最大呢?
例题讲解(3)
小明想用一根长为12米的铁丝围成一个长方形.
长=宽
?
面积:
3.7×2.3=
8.51
面积:
2
×4=8
面积:
3
×3=9
围成正方形时四边形面积最大
小结
(4)在墙边围成一个菜地,使长比宽大4米,问小明围成的菜地的长和宽各是多少呢?(墙面足够长)
例题讲解(4)
小明想用一根长为12米的铁丝围成一个长方形.
铁丝
墙面
x
x+4
解:设此时长方形的宽为x米,
2(2x+x+4)=12
则它的长为(x+4)米,
根据题意,得
长=宽+4
2宽+长=12
用一元一次方程解决实际问题的基本过程和步骤:
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x
=
a)
实际问题的答案
检
验
关键:找出等量关系,将实际问题抽象为方程这一数学模型
归纳总结
审
设
列
解
答
验
等体积变形
?
200
x
80
300
30
200
x
80
300
300
分
析
1:等量关系
2:用字母(未知数x)表示圆钢和长方体的体积
3:根据等量关系列出方程
4:解方程
锻造前圆柱的体积=锻造后长方体的体积
?
?
?
解:设截取圆钢的长度为x厘米,则填写下表
圆柱体
长方体
底面积
高(长)
体积
?
?
?
?
?
?
200
x
80
300
30
解:设截取圆钢的长度为x厘米,则由题意得
?
化简得:3.14x=720,
x≈230。
答:设截取圆钢的长度为230厘米,
1、等积变形问题的等量关系
变形前的体积(周长)=变形后的体积(周长)
小结
2、用方程解决实际问题的基本过程和步骤
再见
人生变幻莫测,但有不变的规则
事件一成不变,却有可变的态度
