2020-2021学年北师大版八年级数学第四章4.1函数 同步练习(word有答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学第四章4.1函数 同步练习(word有答案) | 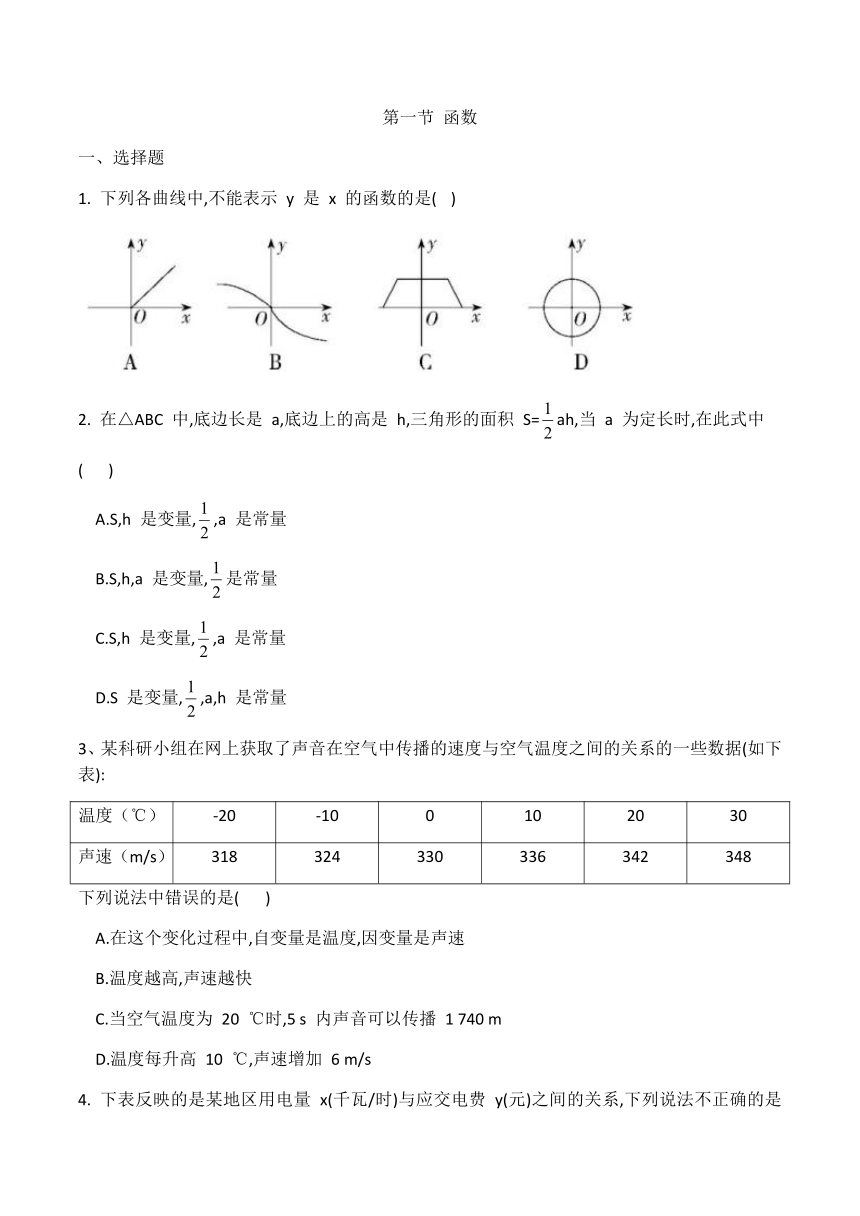 | |
| 格式 | zip | ||
| 文件大小 | 187.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 10:15:27 | ||
图片预览



文档简介
第一节
函数
一、选择题
1.
下列各曲线中,不能表示
y
是
x
的函数的是(
)
2.
在△ABC
中,底边长是
a,底边上的高是
h,三角形的面积
S=ah,当
a
为定长时,在此式中
(
)
A.S,h
是变量,,a
是常量
B.S,h,a
是变量,是常量
C.S,h
是变量,,a
是常量
D.S
是变量,,a,h
是常量
3、某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
温度(℃)
-20
-10
0
10
20
30
声速(m/s)
318
324
330
336
342
348
下列说法中错误的是(
)
A.在这个变化过程中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为
20
℃时,5
s
内声音可以传播
1
740
m
D.温度每升高
10
℃,声速增加
6
m/s
4.
下表反映的是某地区用电量
x(千瓦/时)与应交电费
y(元)之间的关系,下列说法不正确的是(
)
用电量
x(千瓦/时)
1
2
3
4
...
应交电费
y(元)
0.55
1.1
1.65
2.2
...
A.x
与
y
都是变量,且
x
是自变量,y
是
x
的函数
B.用电量每增加
1
千瓦/时,电费增加
0.55
元
C.若用电量为
8
千瓦/时,则应交电费
4.4
元
D.y
不是
x
的函数
5.如图,在矩形
ABCD
中,AB=1,AD=2,M
是
AD
的中点,点
P
在矩形的边上,从点
A
出发,沿
A→B→C→D
运动,到达点
D
后运动终止.设△APM
的面积为
y,点
P
经过的路程为
x,那么能正确表示
y
与
x
之间的函数关系的图象是(
)
6.
甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行
2400
米,先到终点的人原地休息.已知甲先出发
4
分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间
t(分)之间的关系如图所示,下列结论:
①甲步行的速度为
60
米/分;②乙走完全程用了
32
分钟;
③乙用
16
分钟追上甲;④乙到达终点时,甲离终点还有
300
米.其中正确的结论有(
)
A.1
个
B.2
个
C.3
个
D.4
个
7.
已知点
P
为某个封闭图形边界上一定点,动点
M
从点
P
出发,沿其边界顺时针匀速运动一周,设点
M
的运动时间为
x,线段
PM
的长度为
y,y
与
x
之间的函数图象如图所示,则该封闭图形可能是(
)
8.
小鸣和爸爸计划开车从保定到天津去参观“瓷房子”建筑.已知两地相距180千米,且匀速行驶,则汽车行驶时间t(h)与行驶速度v(km/h)之间的函数关系式是?( )
A.t=? ????B.t=180v
C.t=? ????D.t=
9.
已知汽车油箱内有油40
L,每行驶100
km耗油10
L,则汽车行驶过程中油箱内剩余的油量Q(L)与行驶路程s(km)之间的函数表达式是?( )
A.Q=40-? ????B.Q=40+?
C.Q=40-? ????D.Q=40+
二、填空题
10.
某市为鼓励市民节约使用燃气,对燃气进行分段收费,每月使用11立方米以内(包括11立方米)每立方米收费2元,超过部分按每立方米2.4元收取.如果某户使用9立方米燃气,那么燃气费为 ????元;如果某户的燃气使用量是x立方米(x大于11),那么燃气费y与x的函数关系式是 ????.
11.
收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:
波长l(m)
300
500
600
1000
1500
频率f(kHz)
1000
600
500
300
200
观察上表回答:
(1)波长l和频率f数值之间有什么关系?
(2)波长l越大,频率f就越 ????.
12.
下列各式
:①y=0.5x-2;②y=|2x|;③3x+5=y;④y2=2x+8,
其中y是x的函数的有
(只填序号).
13.
在函数
y=中,当
x=-3
时,y=
.
14.
根据如图所示的计算程序计算变量
y
的对应值,若输入变量
x的值为
-,则输出的结果为
.
15.
某机器工作时,油箱中的余油量Q(升)与工作时间t(小时)的关系式为Q=40-6t.当t=3时,Q= ????.
16.
汽车由北京驶往相距840千米的沈阳,汽车的平均速度为每小时70千米,t小时后,汽车距沈阳s千米.
(1)求s与t的函数表达式,并写出自变量t的取值范围;
(2)经过2小时后,汽车距沈阳多少千米?
(3)经过多少小时,汽车距沈阳140千米?
17.
一台拖拉机工作时,每小时耗油6
L,已知油箱中有40
L油.
(1)设拖拉机的工作时间为t(h),油箱中的剩余油量为Q(L),求出Q(L)与t(h)之间的函数关系式,并画出函数图象;
(2)当油箱内剩余10
L油时,这台拖拉机已经工作了几个小时?
答案
1.D
2.A
3.C
4.D
5.A
6.A
7.A
8.A
9.C
10.
18
y=2.4x-4.4
11.
(1)l与f的乘积是一个定值,即lf=300
000,或f=.
(2)波长l越大,频率f就越小.
12.
①②③
13.
14.
-32
15.
22
16.
(1)由题意得s=840-70t(0≤t≤12).
(2)把t=2代入得,s=840-70×2=700.
答:经过2小时后,汽车距沈阳700千米.
(3)把s=140代入得,140=840-70t,解得t=10.
答:经过10小时后,汽车距沈阳140千米.
17.
(1)因为油箱中原有油量为40
L,t小时耗油量为6t
L,所以剩余油量Q(L)与拖拉机工作时间t(h)之间的函数关系式为Q=40-6t.又因为拖拉机工作的最长时间为=h,所以自变量t的取值范围是0≤t≤,所以Q与t之间的函数关系式为Q=40-6t(0≤t≤).
在0≤t≤这个范围内,列表如下:
t
0
2
5
6
Q
40
28
10
4
0
描点、画出函数Q=40-6t(0≤t≤)的图象如图所示.
(2)当Q=10时,10=40-6t,解得t=5,所以当油箱内剩余10
L油时,这台拖拉机已经工作了5个小时.
函数
一、选择题
1.
下列各曲线中,不能表示
y
是
x
的函数的是(
)
2.
在△ABC
中,底边长是
a,底边上的高是
h,三角形的面积
S=ah,当
a
为定长时,在此式中
(
)
A.S,h
是变量,,a
是常量
B.S,h,a
是变量,是常量
C.S,h
是变量,,a
是常量
D.S
是变量,,a,h
是常量
3、某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
温度(℃)
-20
-10
0
10
20
30
声速(m/s)
318
324
330
336
342
348
下列说法中错误的是(
)
A.在这个变化过程中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为
20
℃时,5
s
内声音可以传播
1
740
m
D.温度每升高
10
℃,声速增加
6
m/s
4.
下表反映的是某地区用电量
x(千瓦/时)与应交电费
y(元)之间的关系,下列说法不正确的是(
)
用电量
x(千瓦/时)
1
2
3
4
...
应交电费
y(元)
0.55
1.1
1.65
2.2
...
A.x
与
y
都是变量,且
x
是自变量,y
是
x
的函数
B.用电量每增加
1
千瓦/时,电费增加
0.55
元
C.若用电量为
8
千瓦/时,则应交电费
4.4
元
D.y
不是
x
的函数
5.如图,在矩形
ABCD
中,AB=1,AD=2,M
是
AD
的中点,点
P
在矩形的边上,从点
A
出发,沿
A→B→C→D
运动,到达点
D
后运动终止.设△APM
的面积为
y,点
P
经过的路程为
x,那么能正确表示
y
与
x
之间的函数关系的图象是(
)
6.
甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行
2400
米,先到终点的人原地休息.已知甲先出发
4
分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间
t(分)之间的关系如图所示,下列结论:
①甲步行的速度为
60
米/分;②乙走完全程用了
32
分钟;
③乙用
16
分钟追上甲;④乙到达终点时,甲离终点还有
300
米.其中正确的结论有(
)
A.1
个
B.2
个
C.3
个
D.4
个
7.
已知点
P
为某个封闭图形边界上一定点,动点
M
从点
P
出发,沿其边界顺时针匀速运动一周,设点
M
的运动时间为
x,线段
PM
的长度为
y,y
与
x
之间的函数图象如图所示,则该封闭图形可能是(
)
8.
小鸣和爸爸计划开车从保定到天津去参观“瓷房子”建筑.已知两地相距180千米,且匀速行驶,则汽车行驶时间t(h)与行驶速度v(km/h)之间的函数关系式是?( )
A.t=? ????B.t=180v
C.t=? ????D.t=
9.
已知汽车油箱内有油40
L,每行驶100
km耗油10
L,则汽车行驶过程中油箱内剩余的油量Q(L)与行驶路程s(km)之间的函数表达式是?( )
A.Q=40-? ????B.Q=40+?
C.Q=40-? ????D.Q=40+
二、填空题
10.
某市为鼓励市民节约使用燃气,对燃气进行分段收费,每月使用11立方米以内(包括11立方米)每立方米收费2元,超过部分按每立方米2.4元收取.如果某户使用9立方米燃气,那么燃气费为 ????元;如果某户的燃气使用量是x立方米(x大于11),那么燃气费y与x的函数关系式是 ????.
11.
收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:
波长l(m)
300
500
600
1000
1500
频率f(kHz)
1000
600
500
300
200
观察上表回答:
(1)波长l和频率f数值之间有什么关系?
(2)波长l越大,频率f就越 ????.
12.
下列各式
:①y=0.5x-2;②y=|2x|;③3x+5=y;④y2=2x+8,
其中y是x的函数的有
(只填序号).
13.
在函数
y=中,当
x=-3
时,y=
.
14.
根据如图所示的计算程序计算变量
y
的对应值,若输入变量
x的值为
-,则输出的结果为
.
15.
某机器工作时,油箱中的余油量Q(升)与工作时间t(小时)的关系式为Q=40-6t.当t=3时,Q= ????.
16.
汽车由北京驶往相距840千米的沈阳,汽车的平均速度为每小时70千米,t小时后,汽车距沈阳s千米.
(1)求s与t的函数表达式,并写出自变量t的取值范围;
(2)经过2小时后,汽车距沈阳多少千米?
(3)经过多少小时,汽车距沈阳140千米?
17.
一台拖拉机工作时,每小时耗油6
L,已知油箱中有40
L油.
(1)设拖拉机的工作时间为t(h),油箱中的剩余油量为Q(L),求出Q(L)与t(h)之间的函数关系式,并画出函数图象;
(2)当油箱内剩余10
L油时,这台拖拉机已经工作了几个小时?
答案
1.D
2.A
3.C
4.D
5.A
6.A
7.A
8.A
9.C
10.
18
y=2.4x-4.4
11.
(1)l与f的乘积是一个定值,即lf=300
000,或f=.
(2)波长l越大,频率f就越小.
12.
①②③
13.
14.
-32
15.
22
16.
(1)由题意得s=840-70t(0≤t≤12).
(2)把t=2代入得,s=840-70×2=700.
答:经过2小时后,汽车距沈阳700千米.
(3)把s=140代入得,140=840-70t,解得t=10.
答:经过10小时后,汽车距沈阳140千米.
17.
(1)因为油箱中原有油量为40
L,t小时耗油量为6t
L,所以剩余油量Q(L)与拖拉机工作时间t(h)之间的函数关系式为Q=40-6t.又因为拖拉机工作的最长时间为=h,所以自变量t的取值范围是0≤t≤,所以Q与t之间的函数关系式为Q=40-6t(0≤t≤).
在0≤t≤这个范围内,列表如下:
t
0
2
5
6
Q
40
28
10
4
0
描点、画出函数Q=40-6t(0≤t≤)的图象如图所示.
(2)当Q=10时,10=40-6t,解得t=5,所以当油箱内剩余10
L油时,这台拖拉机已经工作了5个小时.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
