沪科版(2012)初中数学八年级上册 11.2 用坐标表示平移 教案
文档属性
| 名称 | 沪科版(2012)初中数学八年级上册 11.2 用坐标表示平移 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 430.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 00:00:00 | ||
图片预览

文档简介
课题:用坐标表示平移
教学任务分析
教学目标
知识与技能
1、掌握坐标变化与图形平移的关系;2、会根据图形上点的坐标的变化,来判定图形的移动过程。
过程与方法
发展学生的形象思维能力和数形结合的意识,增强几何直观认知能力。
重点
掌握坐标变化与图形平移的关系。
难点
利用坐标变化与图形平移的关系解决实际问题。
教材分析
本节课是强化学生对坐标系的认识的实践案例,也是数形结合思想运用的实践案例,对后续的数学学习起铺垫作用。
学情分析
培养学生探究的兴趣和归纳概括的能力,发展学生的形象思维能力,解决“用坐标表示平移”的初步应用。
教法
讲授法、演示法、练习法
教具
PPT幻灯片、实物投影仪
教学过程设计
问题与情境
师生行为
设计意图
[体验回顾]1.什么叫做平移?把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。2.平移后得到的新图形与原图形有什么关系?平移后图形的位置改变,形状、大小不变。3.投影两个平移过程。
1、回忆平移等知识点;2、投影两个平移过程。
引入本课。
[探究一]从“点的平移”到
“坐标的变化”。(图一)将A点向右分别平移3个单位长、5个单位长度后,点的坐标是什么?
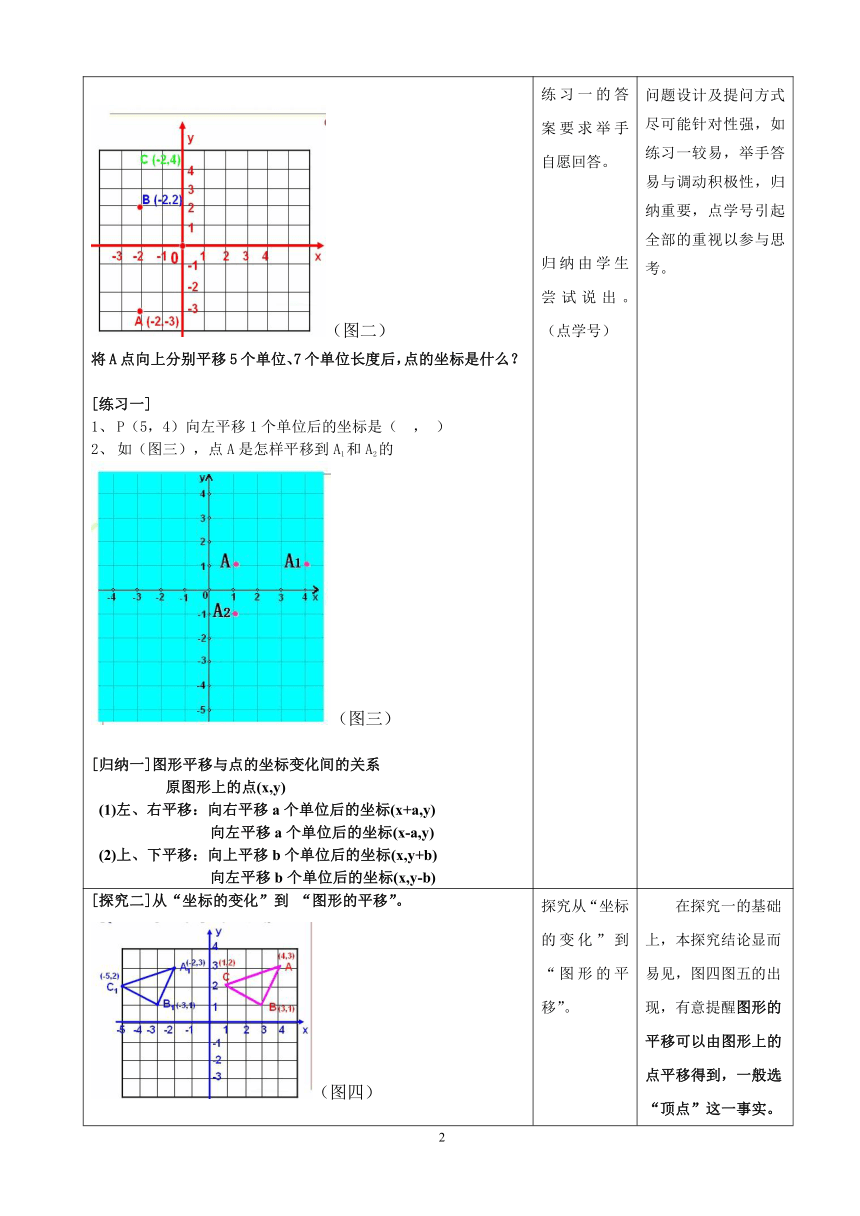
(图二)将A点向上分别平移5个单位、7个单位长度后,点的坐标是什么?
[练习一]P(5,4)向左平移1个单位后的坐标是(
,
)如(图三),点A是怎样平移到A1和A2的(图三)[归纳一]图形平移与点的坐标变化间的关系原图形上的点(x,y)
(1)左、右平移:向右平移a个单位后的坐标(x+a,y)向左平移a个单位后的坐标(x-a,y)
(2)上、下平移:向上平移b个单位后的坐标(x,y+b)向左平移b个单位后的坐标(x,y-b)
探究从“点的平移”到
“坐标的变化”,图一图二分别向右及上方平移,练习一则考虑向左及下方平移的情形。练习一的答案要求举手自愿回答。归纳由学生尝试说出。(点学号)
由简洁入手,让学生了解目标,清晰方向。
问题设计及提问方式尽可能针对性强,如练习一较易,举手答易与调动积极性,归纳重要,点学号引起全部的重视以参与思考。
[探究二]从“坐标的变化”到
“图形的平移”。(图四)从△
ABC到△
A1B2C3,顶点坐标分别发生了什么变化,可以看成图形怎样地变化得到?例1、将△ABC三个顶点的纵坐标都减去5,横坐标不变。写出变化后各顶点坐标,并画出新的图形。此图可以看是由原图怎样变化得到?(图五)注意:图形的平移可以由图形上的点平移得到,一般选“顶点”[练习二]如(图六),三个顶点的横坐标都减去6,纵坐标都减去5。写出变化后各顶点坐标,并画出新的图形。此图是由原图怎样变化得到?(图六)[归纳二]
点的坐标变化与图形平移间的关系原图形上的点(x,y)
(1)横变纵不变:坐标为(x+a,y)点是由原来的点向右平移a个单位而得。(2)纵变横不变:坐标为(x,y+a)点是由原来的点向上平移a个单位而得。(3)坐标系中任何平移,可归结到上下左右的综合情况。
探究从“坐标的变化”到
“图形的平移”。练习二综合横纵都变的情况。选学生作业投影之。归纳可以由个别掌握得好的学生叙述。
在探究一的基础上,本探究结论显而易见,图四图五的出现,有意提醒图形的平移可以由图形上的点平移得到,一般选“顶点”这一事实。
[巩固与提高]快乐之旅线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。有相距5个单位的两点
A(-3,a),B(b,4),AB//x轴,则a=
___
,b=
___
。
(图七)3、如图八△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移到△A1B1C1。求A1、B1、C1的坐标
(图八)4、如图九,图中直角三角形的顶点坐标分别有了什么变化?
本段是学生掌握情况的反馈与提高,调整上课的节奏改变授课的形式,以调动提高课堂参与度。
PAGE
1
教学任务分析
教学目标
知识与技能
1、掌握坐标变化与图形平移的关系;2、会根据图形上点的坐标的变化,来判定图形的移动过程。
过程与方法
发展学生的形象思维能力和数形结合的意识,增强几何直观认知能力。
重点
掌握坐标变化与图形平移的关系。
难点
利用坐标变化与图形平移的关系解决实际问题。
教材分析
本节课是强化学生对坐标系的认识的实践案例,也是数形结合思想运用的实践案例,对后续的数学学习起铺垫作用。
学情分析
培养学生探究的兴趣和归纳概括的能力,发展学生的形象思维能力,解决“用坐标表示平移”的初步应用。
教法
讲授法、演示法、练习法
教具
PPT幻灯片、实物投影仪
教学过程设计
问题与情境
师生行为
设计意图
[体验回顾]1.什么叫做平移?把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。2.平移后得到的新图形与原图形有什么关系?平移后图形的位置改变,形状、大小不变。3.投影两个平移过程。
1、回忆平移等知识点;2、投影两个平移过程。
引入本课。
[探究一]从“点的平移”到
“坐标的变化”。(图一)将A点向右分别平移3个单位长、5个单位长度后,点的坐标是什么?
(图二)将A点向上分别平移5个单位、7个单位长度后,点的坐标是什么?
[练习一]P(5,4)向左平移1个单位后的坐标是(
,
)如(图三),点A是怎样平移到A1和A2的(图三)[归纳一]图形平移与点的坐标变化间的关系原图形上的点(x,y)
(1)左、右平移:向右平移a个单位后的坐标(x+a,y)向左平移a个单位后的坐标(x-a,y)
(2)上、下平移:向上平移b个单位后的坐标(x,y+b)向左平移b个单位后的坐标(x,y-b)
探究从“点的平移”到
“坐标的变化”,图一图二分别向右及上方平移,练习一则考虑向左及下方平移的情形。练习一的答案要求举手自愿回答。归纳由学生尝试说出。(点学号)
由简洁入手,让学生了解目标,清晰方向。
问题设计及提问方式尽可能针对性强,如练习一较易,举手答易与调动积极性,归纳重要,点学号引起全部的重视以参与思考。
[探究二]从“坐标的变化”到
“图形的平移”。(图四)从△
ABC到△
A1B2C3,顶点坐标分别发生了什么变化,可以看成图形怎样地变化得到?例1、将△ABC三个顶点的纵坐标都减去5,横坐标不变。写出变化后各顶点坐标,并画出新的图形。此图可以看是由原图怎样变化得到?(图五)注意:图形的平移可以由图形上的点平移得到,一般选“顶点”[练习二]如(图六),三个顶点的横坐标都减去6,纵坐标都减去5。写出变化后各顶点坐标,并画出新的图形。此图是由原图怎样变化得到?(图六)[归纳二]
点的坐标变化与图形平移间的关系原图形上的点(x,y)
(1)横变纵不变:坐标为(x+a,y)点是由原来的点向右平移a个单位而得。(2)纵变横不变:坐标为(x,y+a)点是由原来的点向上平移a个单位而得。(3)坐标系中任何平移,可归结到上下左右的综合情况。
探究从“坐标的变化”到
“图形的平移”。练习二综合横纵都变的情况。选学生作业投影之。归纳可以由个别掌握得好的学生叙述。
在探究一的基础上,本探究结论显而易见,图四图五的出现,有意提醒图形的平移可以由图形上的点平移得到,一般选“顶点”这一事实。
[巩固与提高]快乐之旅线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。有相距5个单位的两点
A(-3,a),B(b,4),AB//x轴,则a=
___
,b=
___
。
(图七)3、如图八△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移到△A1B1C1。求A1、B1、C1的坐标
(图八)4、如图九,图中直角三角形的顶点坐标分别有了什么变化?
本段是学生掌握情况的反馈与提高,调整上课的节奏改变授课的形式,以调动提高课堂参与度。
PAGE
1
