人教版数学九年级上册24.2.2切线的判定 课件(共21张ppt)
文档属性
| 名称 | 人教版数学九年级上册24.2.2切线的判定 课件(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 221.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 07:09:45 | ||
图片预览




文档简介
(共21张PPT)
切线的判定
.O
l
.O
叫做直线和圆相离
.
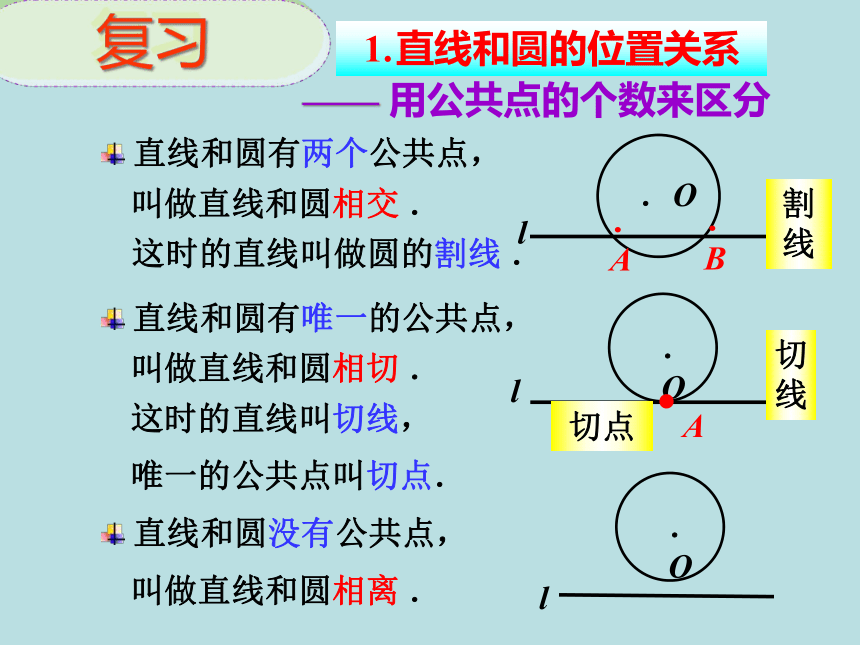
直线和圆没有公共点,
l
直线和圆有唯一的公共点,
叫做直线和圆相切
.
唯一的公共点叫切点.
.O
l
直线和圆有两个公共点,
叫做直线和圆相交
.
这时的直线叫做圆的割线
.
直线和圆的位置关系
.A
.B
切点
割线
——
用公共点的个数来区分
切线
这时的直线叫切线,
A
复习
除了用公共点的个数来区分直线与圆的位置关系外,能否像点和圆的位置关系一样用数量关系的方法来判断直线和圆的位置关系?
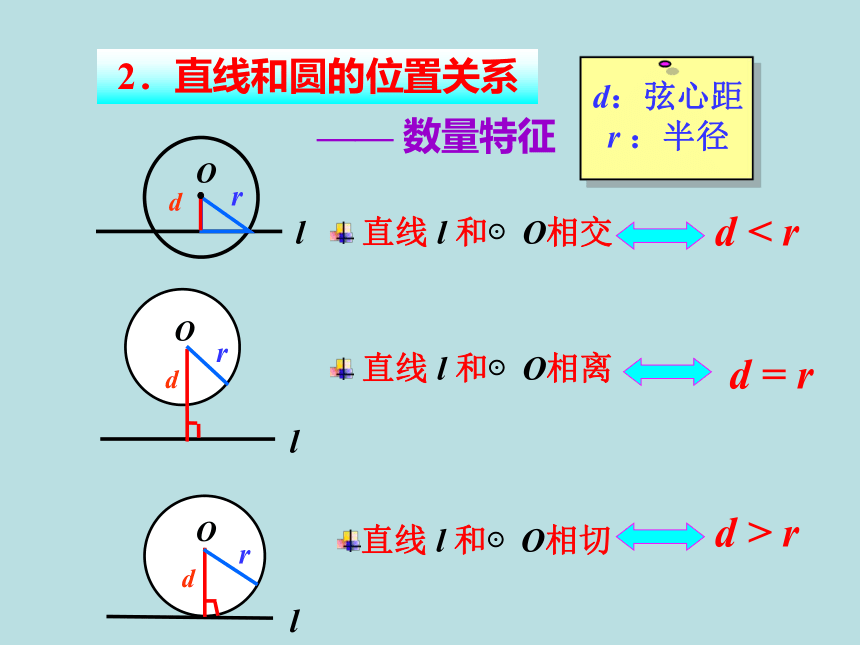
2.直线和圆的位置关系
——
数量特征
r
d
直线
l
和⊙O相交
O
d
r
直线
l
和⊙O相离
d
r
直线
l
和⊙O相切
O
O
l
l
l
d
<
r
d
=
r
d
>
r
d:弦心距
r
:半径
1、已知圆的直径为13cm,设直线和圆心的距离为d
:
3)若d=
8
cm
,则直线与圆______,
直线与圆有____个公共点.
2)若d=6.5cm
,则直线与圆______,
直线与圆有____个公共点.
1)若d=4.5cm
,则直线与圆 ,
直线与圆有____个公共点.
3)若AB和⊙O相交,则
.
2、已知⊙O的半径为5cm,
圆心O与直线AB的距离为d,
根据
条件填写d的范围:
1)若AB和⊙O相离,
则
;
2)若AB和⊙O相切,
则
;
相交
相切
相离
d
>
5cm
d
=
5cm
d
<
5cm
小试牛刀
0cm≤
2
1
0
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质,由_______________________的关系来判断.
(在实际应用中,常采用第二种方法判定)
两
直线
与圆的公共点
圆心到直线的距离与半径
3.知识要点
.
d
r
O
l
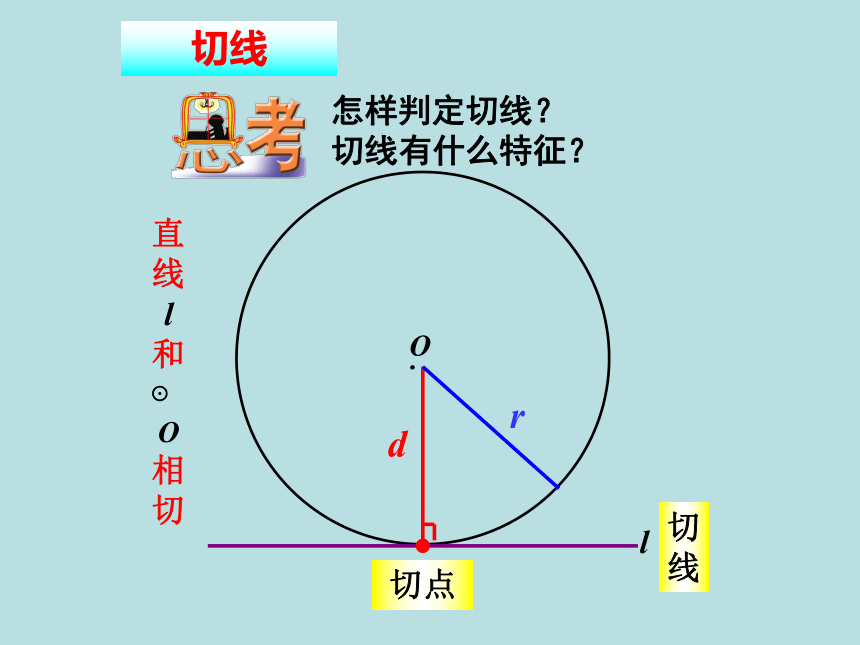
直线
l
和⊙O相切
切线
切点
怎样判定切线?
切线有什么特征?
切线
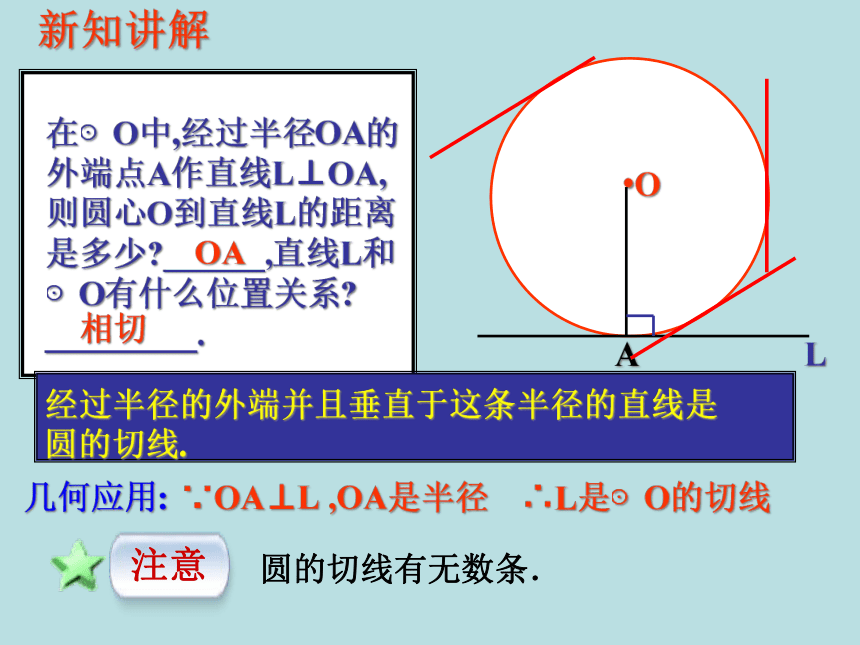
在⊙O中,经过半径OA的
外端点A作直线L⊥OA,
则圆心O到直线L的距离
是多少?______,直线L和
⊙O有什么位置关系?
_________.
新知讲解
.
O
A
OA
相切
L
经过半径的外端并且垂直于这条半径的直线是
圆的切线.
几何应用:
∵OA⊥L
,OA是半径
∴L是⊙O的切线
注意
圆的切线有无数条.
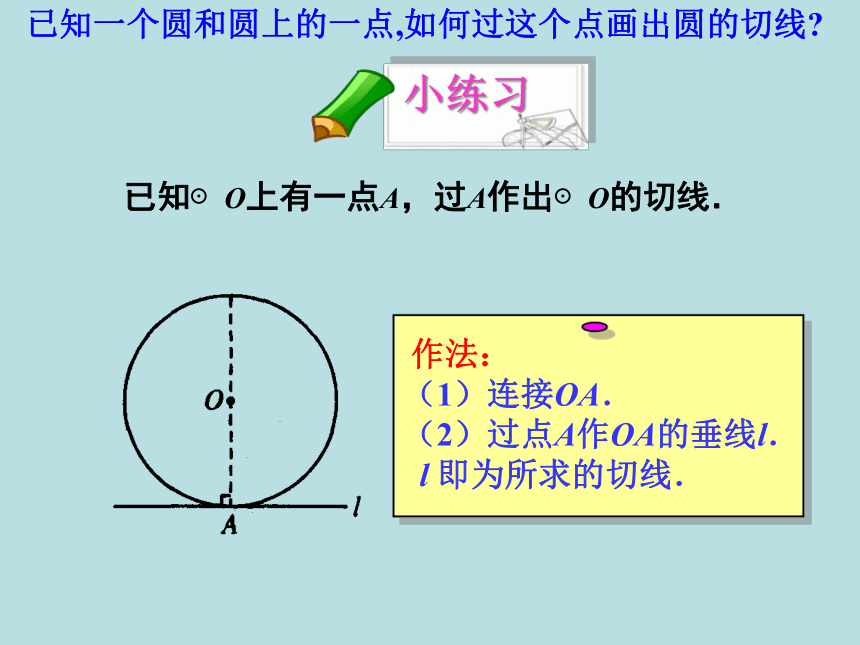
已知⊙O上有一点A,过A作出⊙O的切线.
作法:
(1)连接OA.
(2)过点A作OA的垂线l.
l
即为所求的切线.
小练习
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
判
断
1.
过半径的外端的直线是圆的切线(
)
2.
与半径垂直的的直线是圆的切线(
)
3.
过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。
判断一条直线是圆的切线,你现在会有多少种方法?
有以下三种方法:
1.利用切线的定义:与圆有唯一公共点的直线是圆的切线。
2.利用d与r的关系作判断:当d=r时直线是圆的切线。
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
想一想
〖例1〗
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。
证明:连结OC(如图)。
∵
OA=OB,CA=CB,
∴
OC是等腰三角形OAB底边AB上的中线。
∴
AB⊥OC。
∵
OC是⊙O的半径
∴
AB是⊙O的切线。
有交点,连半径,证垂直
〖例2〗
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
证明:过O作OE⊥AC于E。
∵
AO平分∠BAC,OD⊥AB
∴
OE=OD
∵
OD是⊙O的半径
∴
AC是⊙O的切线。
无交点,作垂直,证半径
O
B
A
C
O
A
B
C
E
D
归纳:
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直.简记为:有交点,连半径,证垂直.
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长.简记为:无交点,作垂直,证半径.
1、如图,△ABC中,AB=AC,AO⊥BC于O,OE⊥AC于E,以O为圆心,OE为半径作⊙O.
求证:AB是⊙O的切线.
F
E
C
O
B
A
巩固:
无交点,作垂直,证半径
2、如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上,
∠CAB=30°.
求证:DC是⊙O的切线.
A
B
C
D
O
有交点,连半径,证垂直
证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C。
∴OP∥AC。
∵PE⊥AC,
∴PE⊥OP。
∴PE为⊙0的切线。
3.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P
PE⊥AC于E。
求证:PE是⊙O的切线。
巩固
O
A
B
C
E
P
(P98)1.
已知:AB是⊙O的直径,∠ABT=45°,
AT=AB.
求证:AT是⊙O的切线.
证明:∵AB=AT,∠ABT=45°
∴∠ATB=∠ABT=45°
∴∠TAB=180°-∠ABT-∠ATB=90°
∴AT⊥AB,
即AT是⊙O的切线.
课堂小结
1.
判定切线的方法有哪些?
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是圆的切线
2.
常用的添辅助线方法?
⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)
l是圆的切线
l是圆的切线
?? 本讲着重介绍了“切线的判定定理”利用此定理判定一条直线是否为
圆的切线时,必须注意直线是否符合题设的两个条件,二者缺一不可.
课堂小结:
??要判定一条直线是圆的切线,我们已学过三种方法.
判定方法
根据
方法1
和圆有唯一公共点的直线是圆的切线
切线定义
方法2
和圆心距离d等于圆的半径r的直线是圆的切线
直线l和⊙O相切
?
?d=r
方法3
过半径外端且和半径垂直的直线是圆的切线
切线判定定理
?在证明一条直线是圆的切线时,常常要添加辅助线,一般有以下两种情况:
(1)如果已知直线过圆上某一点,则可作出过这点的半径,并证明直线与这条半径垂直。
(2)若已知直线和圆的公共点没有确定,这时应过圆心作已知直线的垂线,再证明圆心到直线的距离等于半径。
同圆的切线垂直于经过切点的半径,若题中有切线,就有直角三角形存在。因此解直角三角形与解切线有关的问题有着直接的联系和应用应予以关注。
切线的判定
.O
l
.O
叫做直线和圆相离
.
直线和圆没有公共点,
l
直线和圆有唯一的公共点,
叫做直线和圆相切
.
唯一的公共点叫切点.
.O
l
直线和圆有两个公共点,
叫做直线和圆相交
.
这时的直线叫做圆的割线
.
直线和圆的位置关系
.A
.B
切点
割线
——
用公共点的个数来区分
切线
这时的直线叫切线,
A
复习
除了用公共点的个数来区分直线与圆的位置关系外,能否像点和圆的位置关系一样用数量关系的方法来判断直线和圆的位置关系?
2.直线和圆的位置关系
——
数量特征
r
d
直线
l
和⊙O相交
O
d
r
直线
l
和⊙O相离
d
r
直线
l
和⊙O相切
O
O
l
l
l
d
<
r
d
=
r
d
>
r
d:弦心距
r
:半径
1、已知圆的直径为13cm,设直线和圆心的距离为d
:
3)若d=
8
cm
,则直线与圆______,
直线与圆有____个公共点.
2)若d=6.5cm
,则直线与圆______,
直线与圆有____个公共点.
1)若d=4.5cm
,则直线与圆 ,
直线与圆有____个公共点.
3)若AB和⊙O相交,则
.
2、已知⊙O的半径为5cm,
圆心O与直线AB的距离为d,
根据
条件填写d的范围:
1)若AB和⊙O相离,
则
;
2)若AB和⊙O相切,
则
;
相交
相切
相离
d
>
5cm
d
=
5cm
d
<
5cm
小试牛刀
0cm≤
2
1
0
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质,由_______________________的关系来判断.
(在实际应用中,常采用第二种方法判定)
两
直线
与圆的公共点
圆心到直线的距离与半径
3.知识要点
.
d
r
O
l
直线
l
和⊙O相切
切线
切点
怎样判定切线?
切线有什么特征?
切线
在⊙O中,经过半径OA的
外端点A作直线L⊥OA,
则圆心O到直线L的距离
是多少?______,直线L和
⊙O有什么位置关系?
_________.
新知讲解
.
O
A
OA
相切
L
经过半径的外端并且垂直于这条半径的直线是
圆的切线.
几何应用:
∵OA⊥L
,OA是半径
∴L是⊙O的切线
注意
圆的切线有无数条.
已知⊙O上有一点A,过A作出⊙O的切线.
作法:
(1)连接OA.
(2)过点A作OA的垂线l.
l
即为所求的切线.
小练习
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
判
断
1.
过半径的外端的直线是圆的切线(
)
2.
与半径垂直的的直线是圆的切线(
)
3.
过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。
判断一条直线是圆的切线,你现在会有多少种方法?
有以下三种方法:
1.利用切线的定义:与圆有唯一公共点的直线是圆的切线。
2.利用d与r的关系作判断:当d=r时直线是圆的切线。
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
想一想
〖例1〗
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。
证明:连结OC(如图)。
∵
OA=OB,CA=CB,
∴
OC是等腰三角形OAB底边AB上的中线。
∴
AB⊥OC。
∵
OC是⊙O的半径
∴
AB是⊙O的切线。
有交点,连半径,证垂直
〖例2〗
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
证明:过O作OE⊥AC于E。
∵
AO平分∠BAC,OD⊥AB
∴
OE=OD
∵
OD是⊙O的半径
∴
AC是⊙O的切线。
无交点,作垂直,证半径
O
B
A
C
O
A
B
C
E
D
归纳:
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直.简记为:有交点,连半径,证垂直.
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长.简记为:无交点,作垂直,证半径.
1、如图,△ABC中,AB=AC,AO⊥BC于O,OE⊥AC于E,以O为圆心,OE为半径作⊙O.
求证:AB是⊙O的切线.
F
E
C
O
B
A
巩固:
无交点,作垂直,证半径
2、如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上,
∠CAB=30°.
求证:DC是⊙O的切线.
A
B
C
D
O
有交点,连半径,证垂直
证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C。
∴OP∥AC。
∵PE⊥AC,
∴PE⊥OP。
∴PE为⊙0的切线。
3.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P
PE⊥AC于E。
求证:PE是⊙O的切线。
巩固
O
A
B
C
E
P
(P98)1.
已知:AB是⊙O的直径,∠ABT=45°,
AT=AB.
求证:AT是⊙O的切线.
证明:∵AB=AT,∠ABT=45°
∴∠ATB=∠ABT=45°
∴∠TAB=180°-∠ABT-∠ATB=90°
∴AT⊥AB,
即AT是⊙O的切线.
课堂小结
1.
判定切线的方法有哪些?
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是圆的切线
2.
常用的添辅助线方法?
⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)
l是圆的切线
l是圆的切线
?? 本讲着重介绍了“切线的判定定理”利用此定理判定一条直线是否为
圆的切线时,必须注意直线是否符合题设的两个条件,二者缺一不可.
课堂小结:
??要判定一条直线是圆的切线,我们已学过三种方法.
判定方法
根据
方法1
和圆有唯一公共点的直线是圆的切线
切线定义
方法2
和圆心距离d等于圆的半径r的直线是圆的切线
直线l和⊙O相切
?
?d=r
方法3
过半径外端且和半径垂直的直线是圆的切线
切线判定定理
?在证明一条直线是圆的切线时,常常要添加辅助线,一般有以下两种情况:
(1)如果已知直线过圆上某一点,则可作出过这点的半径,并证明直线与这条半径垂直。
(2)若已知直线和圆的公共点没有确定,这时应过圆心作已知直线的垂线,再证明圆心到直线的距离等于半径。
同圆的切线垂直于经过切点的半径,若题中有切线,就有直角三角形存在。因此解直角三角形与解切线有关的问题有着直接的联系和应用应予以关注。
同课章节目录
