五年级上册数学教案-6.3 梯形面积冀教版
文档属性
| 名称 | 五年级上册数学教案-6.3 梯形面积冀教版 |

|
|
| 格式 | doc | ||
| 文件大小 | 56.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 00:00:00 | ||
图片预览

文档简介
梯形面积 教学设计
教学设计思想:
复习阶段通过让学生把四边形剪去一角,引出各种梯形,既调动了学生学习的积极性,发展学生的思维,又为新课中把一个梯形转化为两个三角形做了铺垫。
在推导梯形面积计算公式时,放手让学生自己将梯形转化为学过的图形,使全体学生处于课堂教学的主体地位,激发学生学习的主动性和创造性。
思考题的设计使梯形的面积计算公式得以广泛的应用,同时也建立了知识之间的联系。
教学目标:
1.知识与技能
理解梯形面积的计算方法,能运用公式正确地计算梯形的面积;
2.过程与方法
通过学生亲自动手拼摆,培养学生的空间观念,发展学生的思维能力;
3.情感态度价值观
通过梯形面积公式的探索过程,进一步感受转化的数学思想;
教学重点:
使学生掌握梯形面积的计算公式;
教学难点:
理解梯形面积计算公式的推导过程;
教具准备:
教具:各种图形的投影片;用吹塑纸剪好两个完全相同的直角梯形、等腰梯形或一般梯形;渠道横截面的实物教具;电脑课件;
学具:每人制做两个完全一样的梯形(直角梯形、等腰梯形或一般梯形)。
教学过程:
教学环节 设计意图 教学预设
一、复习准备 通过让学生动手剪正方形、长方形、平行四边形,激发学生的学习兴趣,在亲自实验中感受图形的变化。 1.出示下列图形
2.提问:
(1)这些分别是什么图形?有什么共同的特征?(都是四边形,都有四个角。)
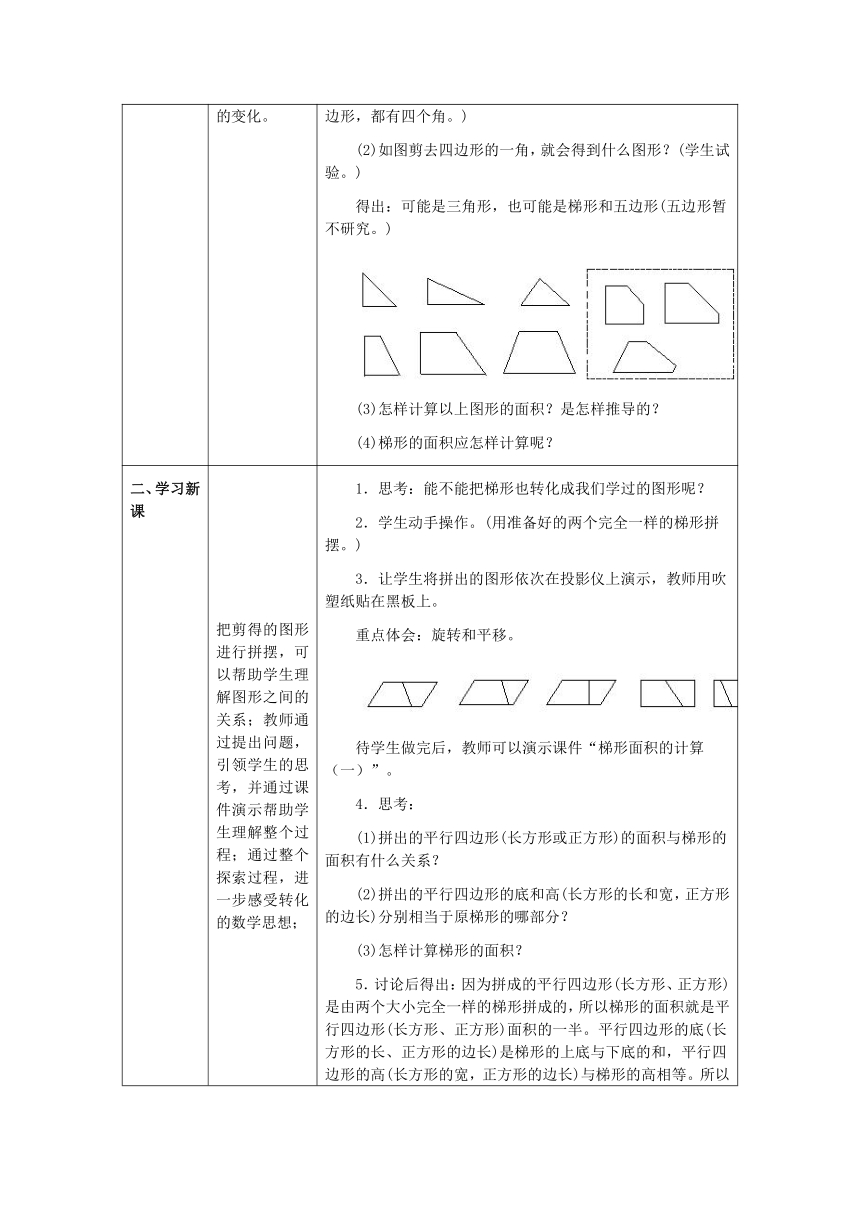
(2)如图剪去四边形的一角,就会得到什么图形?(学生试验。)
得出:可能是三角形,也可能是梯形和五边形(五边形暂不研究。)
(3)怎样计算以上图形的面积?是怎样推导的?
(4)梯形的面积应怎样计算呢?
二、学习新课 把剪得的图形进行拼摆,可以帮助学生理解图形之间的关系;教师通过提出问题,引领学生的思考,并通过课件演示帮助学生理解整个过程;通过整个探索过程,进一步感受转化的数学思想; 1.思考:能不能把梯形也转化成我们学过的图形呢?
2.学生动手操作。(用准备好的两个完全一样的梯形拼摆。)
3.让学生将拼出的图形依次在投影仪上演示,教师用吹塑纸贴在黑板上。
重点体会:旋转和平移。
待学生做完后,教师可以演示课件“梯形面积的计算(一)”。
4.思考:
(1)拼出的平行四边形(长方形或正方形)的面积与梯形的面积有什么关系?
(2)拼出的平行四边形的底和高(长方形的长和宽,正方形的边长)分别相当于原梯形的哪部分?
(3)怎样计算梯形的面积?
5.讨论后得出:因为拼成的平行四边形(长方形、正方形)是由两个大小完全一样的梯形拼成的,所以梯形的面积就是平行四边形(长方形、正方形)面积的一半。平行四边形的底(长方形的长、正方形的边长)是梯形的上底与下底的和,平行四边形的高(长方形的宽,正方形的边长)与梯形的高相等。所以梯形的面积等于上底与下底的和乘以高除以2。
教师板书:
一个梯形的面积=(上底+下底)×高÷2
两个梯形的面积=(上底+下底)×高
平行四边形的面积=底×高
长方形的面积=长×宽
正方形的面积=边长×边长
6.如果用S表示梯形的面积,用a,b和h分别表示梯形的上底、下底和高,那么梯形面积的计算公式应怎样表示?
S=(a+b)h÷2
7.计算梯形的面积。
(1)用面积公式计算。
(3+5)×4÷2
=8×4÷2
=32÷2
=16(平方厘米)
分别说出每步求出的是什么?
为什么要除以2?
3×4÷2+5×4÷2
=(3×4+5×4)÷2
=(3+5)×4÷2
与梯形面积计算公式相符。
三、巩固反馈 通过两个例题,锻炼学生对所学知识的应用能力,发展学生的思维能力;
思考题的设计使梯形的面积计算公式得以广泛的应用,同时也建立了知识之间的联系。 1.出示例题。
一条新挖的渠道,横截面是梯形(如图)。渠口宽2.8米,渠底宽1.4米,渠深1.2米。它的横截面的面积是多少平方米?
(1)出示渠道横截面实物教具,使学生理解渠道横截面是一个梯形,渠口宽就是梯形的上底,渠底宽就是梯形的下底,渠深就是梯形的高。
(2)出示平面图,请学生分别标出梯形的上底,下底和高。
(3)学生试做。
(4)订正。
(2.8+1.4)×1.2÷2
=4.2×1.2÷2
=2.52(平方米)
答:它的横截面的面积是2.52米2。
2.我们经常见到圆木,钢管等堆成下图的形状。求图中圆木的总根数。你有几种解答方法?
学生讨论讲解。
(1)2+3+4+5+6=20(根);
(2)(2+6)+(3+5)+4=8+8+4=20(根);
(3)(2+6)×5÷2=8×5÷2=20(根)。
重点理解解法(3)的算理:
把另外一堆同样形状的钢管倒过来,同原来的一堆接在一起,结果每层的根数就变成同样多,即都等于上下底根数的和。这个和乘以层数得到的根数正好是原来一堆的根数的2倍,所以原来一堆的根数正好是它的一半,即
总根数=(顶层根数+底层根数)×层数÷2
如果把它的横截面看成是梯形,顶层根数相当于上底的长,底层根数相当于下底的长,层数就是梯形的高,求总根数就相当于求梯形的面积。
3.用简便方法计算(思考题)。
(1)小朋友们做游戏,第一排5人,以后每排比前一排多1人,一共排了15排,共有多少小朋友?
(2)计算:1+2+3+…+98+99+100=________。
四、课堂小结 梳理本节课知识。 这节课你收获了哪些知识,还有什么不明白的地方,大家相互说一说。
五、课后作业 教材P103“练一练”2、3题;
教材P107练习五第7、8题。
板书设计:
课题:梯形面积
S=(a+b)h÷2
两个梯形的面积=(上底+下底)×高
(一个)梯形的面积=(上底+下底)×高÷2
平行四边形的面积=底×高
长方形的面积=长×宽
正方形的面积=边长×边长
教学设计思想:
复习阶段通过让学生把四边形剪去一角,引出各种梯形,既调动了学生学习的积极性,发展学生的思维,又为新课中把一个梯形转化为两个三角形做了铺垫。
在推导梯形面积计算公式时,放手让学生自己将梯形转化为学过的图形,使全体学生处于课堂教学的主体地位,激发学生学习的主动性和创造性。
思考题的设计使梯形的面积计算公式得以广泛的应用,同时也建立了知识之间的联系。
教学目标:
1.知识与技能
理解梯形面积的计算方法,能运用公式正确地计算梯形的面积;
2.过程与方法
通过学生亲自动手拼摆,培养学生的空间观念,发展学生的思维能力;
3.情感态度价值观
通过梯形面积公式的探索过程,进一步感受转化的数学思想;
教学重点:
使学生掌握梯形面积的计算公式;
教学难点:
理解梯形面积计算公式的推导过程;
教具准备:
教具:各种图形的投影片;用吹塑纸剪好两个完全相同的直角梯形、等腰梯形或一般梯形;渠道横截面的实物教具;电脑课件;
学具:每人制做两个完全一样的梯形(直角梯形、等腰梯形或一般梯形)。
教学过程:
教学环节 设计意图 教学预设
一、复习准备 通过让学生动手剪正方形、长方形、平行四边形,激发学生的学习兴趣,在亲自实验中感受图形的变化。 1.出示下列图形
2.提问:
(1)这些分别是什么图形?有什么共同的特征?(都是四边形,都有四个角。)
(2)如图剪去四边形的一角,就会得到什么图形?(学生试验。)
得出:可能是三角形,也可能是梯形和五边形(五边形暂不研究。)
(3)怎样计算以上图形的面积?是怎样推导的?
(4)梯形的面积应怎样计算呢?
二、学习新课 把剪得的图形进行拼摆,可以帮助学生理解图形之间的关系;教师通过提出问题,引领学生的思考,并通过课件演示帮助学生理解整个过程;通过整个探索过程,进一步感受转化的数学思想; 1.思考:能不能把梯形也转化成我们学过的图形呢?
2.学生动手操作。(用准备好的两个完全一样的梯形拼摆。)
3.让学生将拼出的图形依次在投影仪上演示,教师用吹塑纸贴在黑板上。
重点体会:旋转和平移。
待学生做完后,教师可以演示课件“梯形面积的计算(一)”。
4.思考:
(1)拼出的平行四边形(长方形或正方形)的面积与梯形的面积有什么关系?
(2)拼出的平行四边形的底和高(长方形的长和宽,正方形的边长)分别相当于原梯形的哪部分?
(3)怎样计算梯形的面积?
5.讨论后得出:因为拼成的平行四边形(长方形、正方形)是由两个大小完全一样的梯形拼成的,所以梯形的面积就是平行四边形(长方形、正方形)面积的一半。平行四边形的底(长方形的长、正方形的边长)是梯形的上底与下底的和,平行四边形的高(长方形的宽,正方形的边长)与梯形的高相等。所以梯形的面积等于上底与下底的和乘以高除以2。
教师板书:
一个梯形的面积=(上底+下底)×高÷2
两个梯形的面积=(上底+下底)×高
平行四边形的面积=底×高
长方形的面积=长×宽
正方形的面积=边长×边长
6.如果用S表示梯形的面积,用a,b和h分别表示梯形的上底、下底和高,那么梯形面积的计算公式应怎样表示?
S=(a+b)h÷2
7.计算梯形的面积。
(1)用面积公式计算。
(3+5)×4÷2
=8×4÷2
=32÷2
=16(平方厘米)
分别说出每步求出的是什么?
为什么要除以2?
3×4÷2+5×4÷2
=(3×4+5×4)÷2
=(3+5)×4÷2
与梯形面积计算公式相符。
三、巩固反馈 通过两个例题,锻炼学生对所学知识的应用能力,发展学生的思维能力;
思考题的设计使梯形的面积计算公式得以广泛的应用,同时也建立了知识之间的联系。 1.出示例题。
一条新挖的渠道,横截面是梯形(如图)。渠口宽2.8米,渠底宽1.4米,渠深1.2米。它的横截面的面积是多少平方米?
(1)出示渠道横截面实物教具,使学生理解渠道横截面是一个梯形,渠口宽就是梯形的上底,渠底宽就是梯形的下底,渠深就是梯形的高。
(2)出示平面图,请学生分别标出梯形的上底,下底和高。
(3)学生试做。
(4)订正。
(2.8+1.4)×1.2÷2
=4.2×1.2÷2
=2.52(平方米)
答:它的横截面的面积是2.52米2。
2.我们经常见到圆木,钢管等堆成下图的形状。求图中圆木的总根数。你有几种解答方法?
学生讨论讲解。
(1)2+3+4+5+6=20(根);
(2)(2+6)+(3+5)+4=8+8+4=20(根);
(3)(2+6)×5÷2=8×5÷2=20(根)。
重点理解解法(3)的算理:
把另外一堆同样形状的钢管倒过来,同原来的一堆接在一起,结果每层的根数就变成同样多,即都等于上下底根数的和。这个和乘以层数得到的根数正好是原来一堆的根数的2倍,所以原来一堆的根数正好是它的一半,即
总根数=(顶层根数+底层根数)×层数÷2
如果把它的横截面看成是梯形,顶层根数相当于上底的长,底层根数相当于下底的长,层数就是梯形的高,求总根数就相当于求梯形的面积。
3.用简便方法计算(思考题)。
(1)小朋友们做游戏,第一排5人,以后每排比前一排多1人,一共排了15排,共有多少小朋友?
(2)计算:1+2+3+…+98+99+100=________。
四、课堂小结 梳理本节课知识。 这节课你收获了哪些知识,还有什么不明白的地方,大家相互说一说。
五、课后作业 教材P103“练一练”2、3题;
教材P107练习五第7、8题。
板书设计:
课题:梯形面积
S=(a+b)h÷2
两个梯形的面积=(上底+下底)×高
(一个)梯形的面积=(上底+下底)×高÷2
平行四边形的面积=底×高
长方形的面积=长×宽
正方形的面积=边长×边长
