人教版七年级上册数学 3.1.2 等式的性质课件(20张)
文档属性
| 名称 | 人教版七年级上册数学 3.1.2 等式的性质课件(20张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 15:09:38 | ||
图片预览








文档简介
一元一次方程
?
第三章
3.1.2 等式的性质
核心目标
……………..…
2
1
课前学案
……………..…
3
课堂导案
……………..…
4
5
课后练案
……………..…
能力培优
……………..…
核心目标
掌握等式的性质,会用等式的性质解简单的一元一次方程.
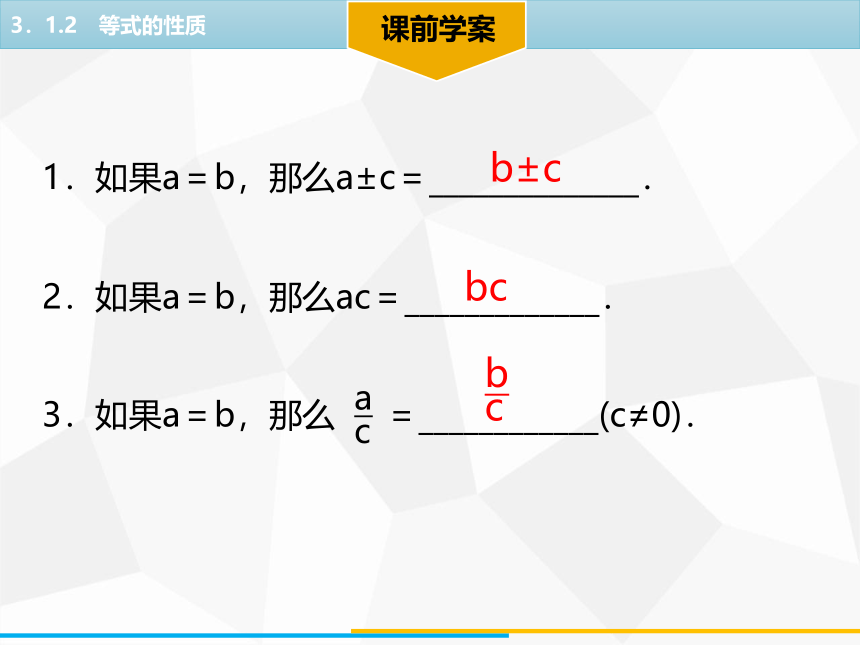
课前学案
1.如果a=b,那么a±c=______________.
2.如果a=b,那么ac=_____________.
a
c
3.如果a=b,那么 =____________(c≠0).
bc
b±c
b
c
课堂导案
【答案】D
【解析】利用等式的性质对每个等式进行变形即可得答案.
【点拔】此题考查了等式的基本性质,正确把握等式的基本性质是解题关键.
知识点1:等式的性质
【例1】若a=b,那么下列各式不一定成立的是( )
A.a-3=b-3 B.-4a=-4b
C.3a-1=3b-1 D. =
a
c
b
c
D
课堂导案
D
对点训练一
1.已知a=b,则下列变形不正确的是( )
A.a+2=b+2 B.-3a=-3b
C. = D.a+5=b-5
a
7
b
7
2.已知ax=ay,下列变形不正确的是( )
A.x=y B.ax+1=ay+1
C.2ax=2ay D.3-ax=3-ay
A
课堂导案
3.用适当的数或式子填空:
(1)若2x-3=4,则2x=__________;
(2)若2a+b=3,则2a=3__________;
(3)若3x=6,则x=__________;
7
-b
2
1
3
(4)若 x+2=1,则x+6=__________.
3
课堂导案
知识点2:利用等式性质解方程
【例2】解方程:- x+2=4.
1
2
【答案】解:两边减2,得- +2-2=4-2,
即- x=2.两边乘以-2,得x=-4.
1
2
1
2
【点拔】利用等式性质解方程,应设法使方程两边化为“ax=b”的形式,然后化为“x= ”的形式,从而得出方程的解.
b
a
【解析】先把未知项单独放在左边,两边都减去2,再由于- x=2求x,两边乘以-2.
1
2
课堂导案
对点训练二
4.利用等式性质解方程:
(1)x-5=6; (2)3x-4=5;
x=6+5 ? 3x=5+4
x=11 x=9÷3
x= 3
课堂导案
1
2
(3) x+3=7.
x =7-3
x =4?2
x=8
1
2
课后练案
C
5.下列变形符合等式的性质的是( )
A.由 =0,得x=3
B.由-2x=6,得x=3
C.由x-1=3,得x=4
D.由x=2x,得1=2
x
3
课后练案
B
a
c
6.下列变形中,正确的是( )
A.若ac=bc,则a=b
B.若 = ,则a=b
C.若a2=b2,则a=b
D.若 -x=6,则x=-2
b
c
1
3
课后练案
C
7.下列变形不一定成立的是( )
A.由x=y,则x+5=y+5
B.由a=b,得ac=bc
C.由x=y,则 =
D.由 = ,得x=y
x
a
y
a
x
a
y
a
课后练案
D
8.下列变形正确的是( )
A. x=0变形得x=3
B.3x=2x-2变形得3x-2x=2
C.3x=2变形得x=
D. x-1=x变形得2x-3=3x
1
3
3
2
2
3
课后练案
9.(1)已知2x-1=4,两边同时_________,得2x=5.
(2)已知-5x=-5y,两边同时_________________,得x=y.
乘以-4
加1
除以-5
1
4
(3)已知- x=2y,两边同时__________________,得x=-8y.
课后练案
10.用适当的数或式子填空:
(1)若2x-1=7,则2x=7+__________;
(2)若2x+3=5,则2x=5-__________;
(3)若3x=5x-8则-2x=__________;
5
1
3
-8
1
5
(4)若 x+2=1,则x+10=__________.
课后练案
11.(1)若3x+5=2,则3x=2-________,这是根据等式性质________.
1
5
2
-
1
12
12.利用等式性质解下列方程.
(1)3x+4=10
3x =10-4
x =6÷3
x=2
?
1
3
(2)若-4x= ,则x=________,这是根据等式性质_________.
课后练案
? (2) x-2=1
1
3
? (3)- x-10=2.
1
3
x =3
x =3?3
x=9
1
3
- x =12
x =12?(-3)
x=-36
1
3
能力培优
13.对于任意有理数a、b、c、d,我们规定| |
=ad-bc,如| |=1×4-2×3,若| | =-2,试用等式的基本性质求x的值.
a b
c d
1 2
3 4
x-2
3-4
由题意,得-4x+6=-2.
方程两边同时减6,得-4x=-8.
方程两边同时除以-4,得x=2.
感谢聆听
?
第三章
3.1.2 等式的性质
核心目标
……………..…
2
1
课前学案
……………..…
3
课堂导案
……………..…
4
5
课后练案
……………..…
能力培优
……………..…
核心目标
掌握等式的性质,会用等式的性质解简单的一元一次方程.
课前学案
1.如果a=b,那么a±c=______________.
2.如果a=b,那么ac=_____________.
a
c
3.如果a=b,那么 =____________(c≠0).
bc
b±c
b
c
课堂导案
【答案】D
【解析】利用等式的性质对每个等式进行变形即可得答案.
【点拔】此题考查了等式的基本性质,正确把握等式的基本性质是解题关键.
知识点1:等式的性质
【例1】若a=b,那么下列各式不一定成立的是( )
A.a-3=b-3 B.-4a=-4b
C.3a-1=3b-1 D. =
a
c
b
c
D
课堂导案
D
对点训练一
1.已知a=b,则下列变形不正确的是( )
A.a+2=b+2 B.-3a=-3b
C. = D.a+5=b-5
a
7
b
7
2.已知ax=ay,下列变形不正确的是( )
A.x=y B.ax+1=ay+1
C.2ax=2ay D.3-ax=3-ay
A
课堂导案
3.用适当的数或式子填空:
(1)若2x-3=4,则2x=__________;
(2)若2a+b=3,则2a=3__________;
(3)若3x=6,则x=__________;
7
-b
2
1
3
(4)若 x+2=1,则x+6=__________.
3
课堂导案
知识点2:利用等式性质解方程
【例2】解方程:- x+2=4.
1
2
【答案】解:两边减2,得- +2-2=4-2,
即- x=2.两边乘以-2,得x=-4.
1
2
1
2
【点拔】利用等式性质解方程,应设法使方程两边化为“ax=b”的形式,然后化为“x= ”的形式,从而得出方程的解.
b
a
【解析】先把未知项单独放在左边,两边都减去2,再由于- x=2求x,两边乘以-2.
1
2
课堂导案
对点训练二
4.利用等式性质解方程:
(1)x-5=6; (2)3x-4=5;
x=6+5 ? 3x=5+4
x=11 x=9÷3
x= 3
课堂导案
1
2
(3) x+3=7.
x =7-3
x =4?2
x=8
1
2
课后练案
C
5.下列变形符合等式的性质的是( )
A.由 =0,得x=3
B.由-2x=6,得x=3
C.由x-1=3,得x=4
D.由x=2x,得1=2
x
3
课后练案
B
a
c
6.下列变形中,正确的是( )
A.若ac=bc,则a=b
B.若 = ,则a=b
C.若a2=b2,则a=b
D.若 -x=6,则x=-2
b
c
1
3
课后练案
C
7.下列变形不一定成立的是( )
A.由x=y,则x+5=y+5
B.由a=b,得ac=bc
C.由x=y,则 =
D.由 = ,得x=y
x
a
y
a
x
a
y
a
课后练案
D
8.下列变形正确的是( )
A. x=0变形得x=3
B.3x=2x-2变形得3x-2x=2
C.3x=2变形得x=
D. x-1=x变形得2x-3=3x
1
3
3
2
2
3
课后练案
9.(1)已知2x-1=4,两边同时_________,得2x=5.
(2)已知-5x=-5y,两边同时_________________,得x=y.
乘以-4
加1
除以-5
1
4
(3)已知- x=2y,两边同时__________________,得x=-8y.
课后练案
10.用适当的数或式子填空:
(1)若2x-1=7,则2x=7+__________;
(2)若2x+3=5,则2x=5-__________;
(3)若3x=5x-8则-2x=__________;
5
1
3
-8
1
5
(4)若 x+2=1,则x+10=__________.
课后练案
11.(1)若3x+5=2,则3x=2-________,这是根据等式性质________.
1
5
2
-
1
12
12.利用等式性质解下列方程.
(1)3x+4=10
3x =10-4
x =6÷3
x=2
?
1
3
(2)若-4x= ,则x=________,这是根据等式性质_________.
课后练案
? (2) x-2=1
1
3
? (3)- x-10=2.
1
3
x =3
x =3?3
x=9
1
3
- x =12
x =12?(-3)
x=-36
1
3
能力培优
13.对于任意有理数a、b、c、d,我们规定| |
=ad-bc,如| |=1×4-2×3,若| | =-2,试用等式的基本性质求x的值.
a b
c d
1 2
3 4
x-2
3-4
由题意,得-4x+6=-2.
方程两边同时减6,得-4x=-8.
方程两边同时除以-4,得x=2.
感谢聆听
