人教版八年级上册数学 15.1.2 分式的基本性质课件(24张)
文档属性
| 名称 | 人教版八年级上册数学 15.1.2 分式的基本性质课件(24张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 15:38:55 | ||
图片预览








文档简介
分式
?
第十五章
15.1.2 分式的基本性质
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
了解分式的基本性质,掌握分式的约分与通分.
课前学案
1.分式的分子与分母同乘(或除以)同一个不等于0的整式,分式的值__________.
2.利用分式的基本性质,约去分式的分子和分母的公因式,不改变分式的值,这种分式变形叫做_________.
不变
约分
课前学案
3.一般取各分母的所有因式______________的积作为公分母,它叫做最简公分母.
4.把几个异分母的分式分别化为与原来的分式相等的同分母的分式,这样的分式变形叫做__________.
最高次幂
通分
课堂导案
【例1】下列式子从左到右的变形一定正确的是( )
C
课堂导案
【解析】分式的基本性质是分式的分子、分母同时乘以或除以同一个非0的数或式子,分式的值不变.而如果分式的分子、分母同时加上或减去同一个非0的数或式子,分式的值改变.
【答案】C
【点拔】此题主要考查了分式的性质.注意约分是约去分子、分母的公因式,并且分子与分母相同时约分结果应是1,而不是0.
课堂导案
1.下列各式从左到右的变形正确的是( )
D
A
课堂导案
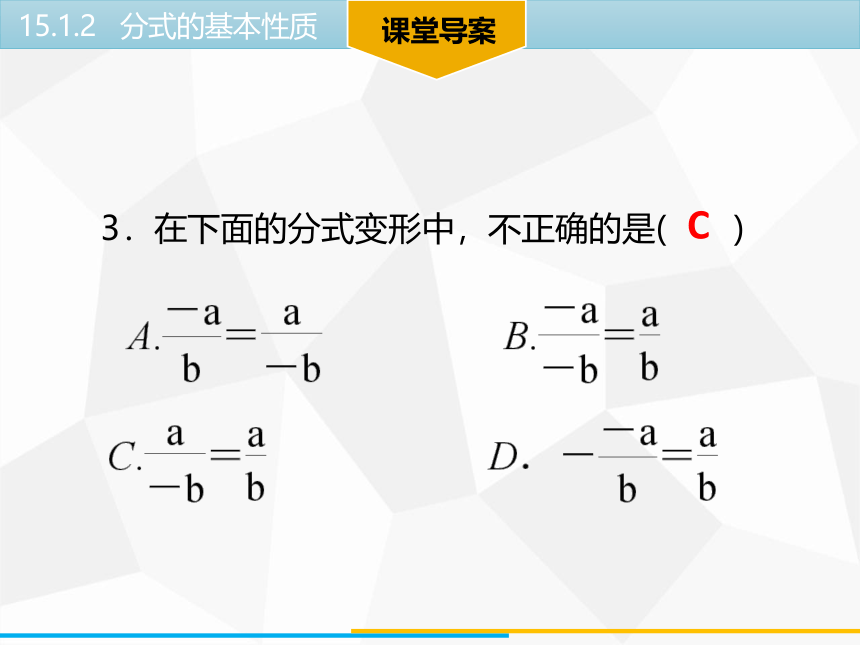
3.在下面的分式变形中,不正确的是( )
C
课堂导案
B
课堂导案
【答案】B
【点拔】此题考查了约分,把要求的式子进行变形,再分子与分母进行约分是解题的关键,注意约分时一定约到最简.
课堂导案
②
2a
课堂导案
课堂导案
【答案】解:最简公分母是2(x+3)(x-3).
课堂导案
【点拔】通分的关键是确定最简公分母,最简公分母的系数取各分母系数的最小公倍数,最简公分母的字母因式取各分母所有字母的最高次幂的积.
【解析】找到最简公分母,分子、分母同时乘以分母中缺少的项,即可通分.
课堂导案
课后练案
9.下列等式中,正确的是( )
A. = B. =
C. = D. =
a
b
2a
2b
a
b
a-1
b-1
a
b
a+1
b+1
a
b
a2
b2
10.若把分式 中x、y都扩大3倍,
那么分式的值( )
A.扩大3倍 B.不变
C.缩小3倍 D.缩小6倍
5xy
x+y
A
A
课后练案
11.下列分式是最简分式的是( )
A. B.
C. D.
2a
3a2b
a+b
a2+b2
a
a2-3a
a2-ab
a2-b2
12.分式 , , 的最简公分母是( )
A.24a2b3 B.24ab2
C.12ab2 D.12a2b3
b
2a
x
3b2
1
4ab
B
C
14.约分: =_________, =______.
3a2b
6ab2c
x+2
xy+2y
15.化简: =_______, =_______.
x2-x
1-x
xy-2y
x2-4x+4
课后练案
13.不改变分式的值,使分式的分子与分母都不含负号: =_________,- =_________.
-5x
2y
2x
-3y
5x
2y
-
2x
3y
a
2bc
1
y
-x
y
x-2
课后练案
16.通分:
(1) 与 ;
2c
a2b
c
3ab
课后练案
a-1
a2+2a+1
3
a2-1
(2) 与 .
课后练案
17.先化简再求值: ,其中m=2,n=1.
2m2-4mn+2n2
m2-n2
能力培优
18.若abc≠0,求m= + + 的值.
a
|a|
|b|
b
c
|c|
(1)当a>0,b>0,c>0时,原式= + + =3.
(2)当a>0,b>0,c<0时,原式= + - =1.
(3)当a>0,b<0,c<0时,原式= - - =-1.
(4) 当a<0,b<0,c<0时,原式=- - - =-3.
a
a
b
b
c
c
a
a
b
b
c
c
a
a
b
b
c
c
a
a
b
b
c
c
感谢聆听
?
第十五章
15.1.2 分式的基本性质
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
了解分式的基本性质,掌握分式的约分与通分.
课前学案
1.分式的分子与分母同乘(或除以)同一个不等于0的整式,分式的值__________.
2.利用分式的基本性质,约去分式的分子和分母的公因式,不改变分式的值,这种分式变形叫做_________.
不变
约分
课前学案
3.一般取各分母的所有因式______________的积作为公分母,它叫做最简公分母.
4.把几个异分母的分式分别化为与原来的分式相等的同分母的分式,这样的分式变形叫做__________.
最高次幂
通分
课堂导案
【例1】下列式子从左到右的变形一定正确的是( )
C
课堂导案
【解析】分式的基本性质是分式的分子、分母同时乘以或除以同一个非0的数或式子,分式的值不变.而如果分式的分子、分母同时加上或减去同一个非0的数或式子,分式的值改变.
【答案】C
【点拔】此题主要考查了分式的性质.注意约分是约去分子、分母的公因式,并且分子与分母相同时约分结果应是1,而不是0.
课堂导案
1.下列各式从左到右的变形正确的是( )
D
A
课堂导案
3.在下面的分式变形中,不正确的是( )
C
课堂导案
B
课堂导案
【答案】B
【点拔】此题考查了约分,把要求的式子进行变形,再分子与分母进行约分是解题的关键,注意约分时一定约到最简.
课堂导案
②
2a
课堂导案
课堂导案
【答案】解:最简公分母是2(x+3)(x-3).
课堂导案
【点拔】通分的关键是确定最简公分母,最简公分母的系数取各分母系数的最小公倍数,最简公分母的字母因式取各分母所有字母的最高次幂的积.
【解析】找到最简公分母,分子、分母同时乘以分母中缺少的项,即可通分.
课堂导案
课后练案
9.下列等式中,正确的是( )
A. = B. =
C. = D. =
a
b
2a
2b
a
b
a-1
b-1
a
b
a+1
b+1
a
b
a2
b2
10.若把分式 中x、y都扩大3倍,
那么分式的值( )
A.扩大3倍 B.不变
C.缩小3倍 D.缩小6倍
5xy
x+y
A
A
课后练案
11.下列分式是最简分式的是( )
A. B.
C. D.
2a
3a2b
a+b
a2+b2
a
a2-3a
a2-ab
a2-b2
12.分式 , , 的最简公分母是( )
A.24a2b3 B.24ab2
C.12ab2 D.12a2b3
b
2a
x
3b2
1
4ab
B
C
14.约分: =_________, =______.
3a2b
6ab2c
x+2
xy+2y
15.化简: =_______, =_______.
x2-x
1-x
xy-2y
x2-4x+4
课后练案
13.不改变分式的值,使分式的分子与分母都不含负号: =_________,- =_________.
-5x
2y
2x
-3y
5x
2y
-
2x
3y
a
2bc
1
y
-x
y
x-2
课后练案
16.通分:
(1) 与 ;
2c
a2b
c
3ab
课后练案
a-1
a2+2a+1
3
a2-1
(2) 与 .
课后练案
17.先化简再求值: ,其中m=2,n=1.
2m2-4mn+2n2
m2-n2
能力培优
18.若abc≠0,求m= + + 的值.
a
|a|
|b|
b
c
|c|
(1)当a>0,b>0,c>0时,原式= + + =3.
(2)当a>0,b>0,c<0时,原式= + - =1.
(3)当a>0,b<0,c<0时,原式= - - =-1.
(4) 当a<0,b<0,c<0时,原式=- - - =-3.
a
a
b
b
c
c
a
a
b
b
c
c
a
a
b
b
c
c
a
a
b
b
c
c
感谢聆听
