人教版七年级上册数学 4.3.2 角的比较与运算课件(25张)
文档属性
| 名称 | 人教版七年级上册数学 4.3.2 角的比较与运算课件(25张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 18:17:36 | ||
图片预览



文档简介
几何图形初步
?
第四章
4.3.2 角的比较与运算
核心目标
……………..…
2
1
课前学案
……………..…
3
课堂导案
……………..…
4
5
课后练案
……………..…
能力培优
……………..…
核心目标
进会比较角的大小,认识角的平分线,会根据几何图形进行角的和、差、倍、分等运算.
课前学案
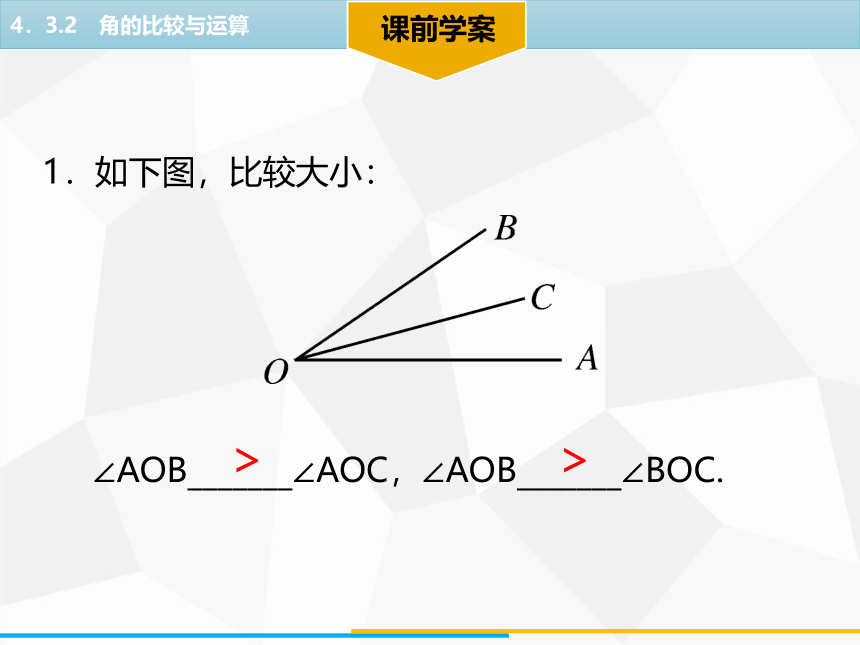
1.如下图,比较大小:
∠AOB_______∠AOC,∠AOB_______∠BOC.
>
>
课前学案
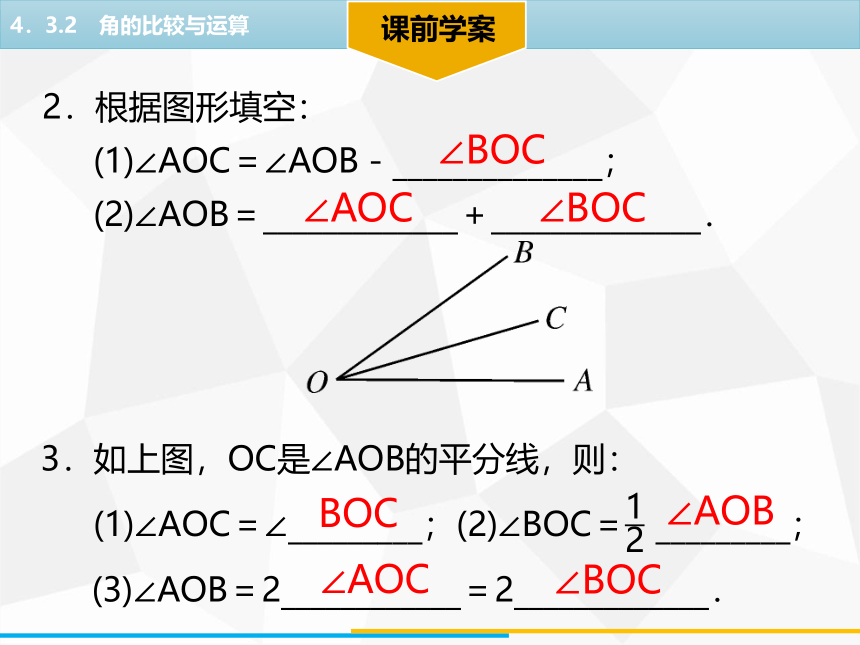
2.根据图形填空:
(1)∠AOC=∠AOB-______________;
(2)∠AOB=_____________+______________.
3.如上图,OC是∠AOB的平分线,则:
(1)∠AOC=∠_________;(2)∠BOC= _________;
(3)∠AOB=2____________=2_____________.
1
2
∠BOC
BOC
∠AOB
∠AOC
∠BOC
∠AOC
∠BOC
课堂导案
知识点1:角的和差与大小比较
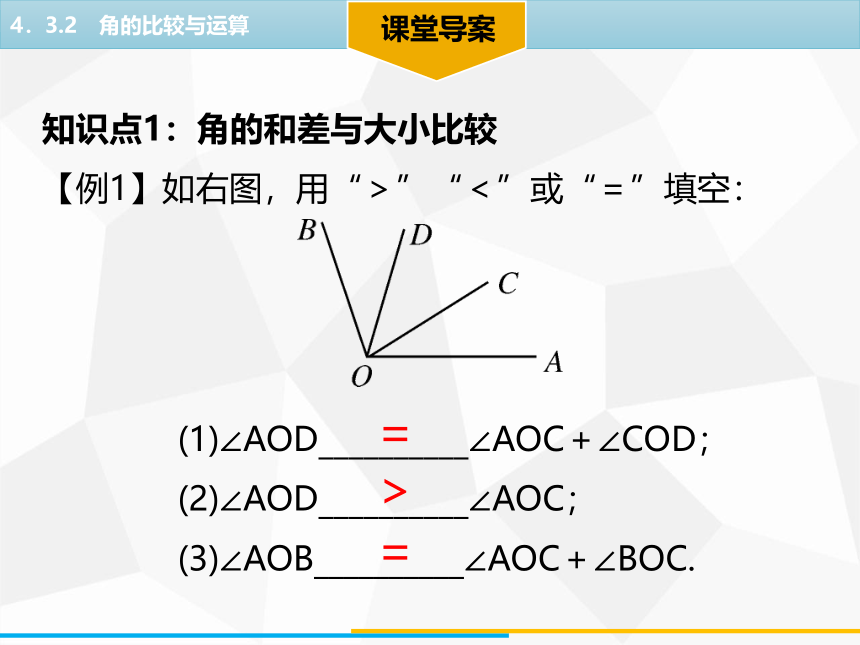
【例1】如右图,用“>”“<”或“=”填空:
?
(1)∠AOD__________∠AOC+∠COD;
(2)∠AOD__________∠AOC;
(3)∠AOB__________∠AOC+∠BOC.
=
>
=
课堂导案
【答案】(1)= (2)> (3)=
【解析】由图形中的角的关系易得出结果.
【点拔】充分利用图形中角的和差关系来确定角的大小数量关系.
课堂导案
对点训练一
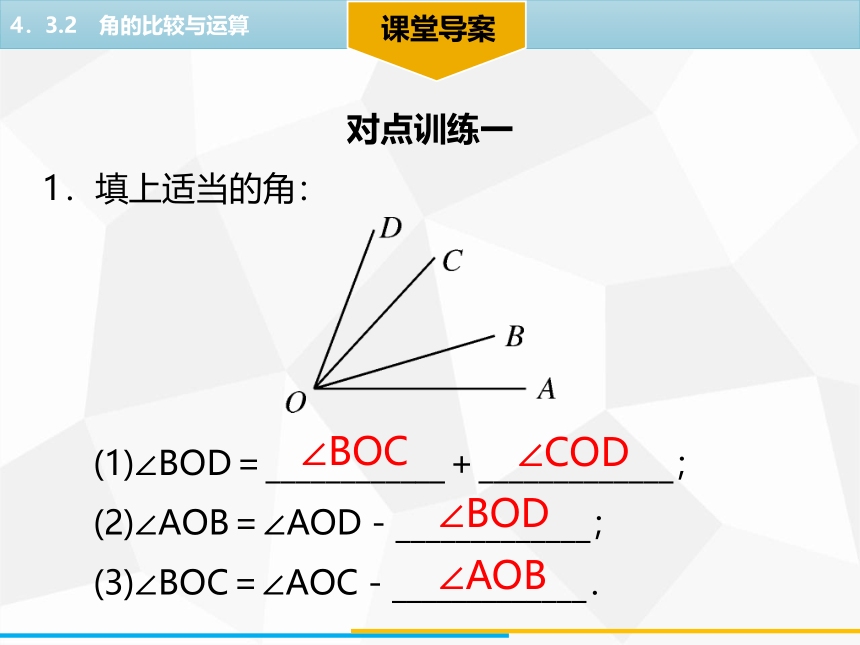
1.填上适当的角:
(1)∠BOD=____________+_____________;
(2)∠AOB=∠AOD-_____________;
(3)∠BOC=∠AOC-_____________.
∠BOC
∠BOD
∠COD
∠AOB
课堂导案
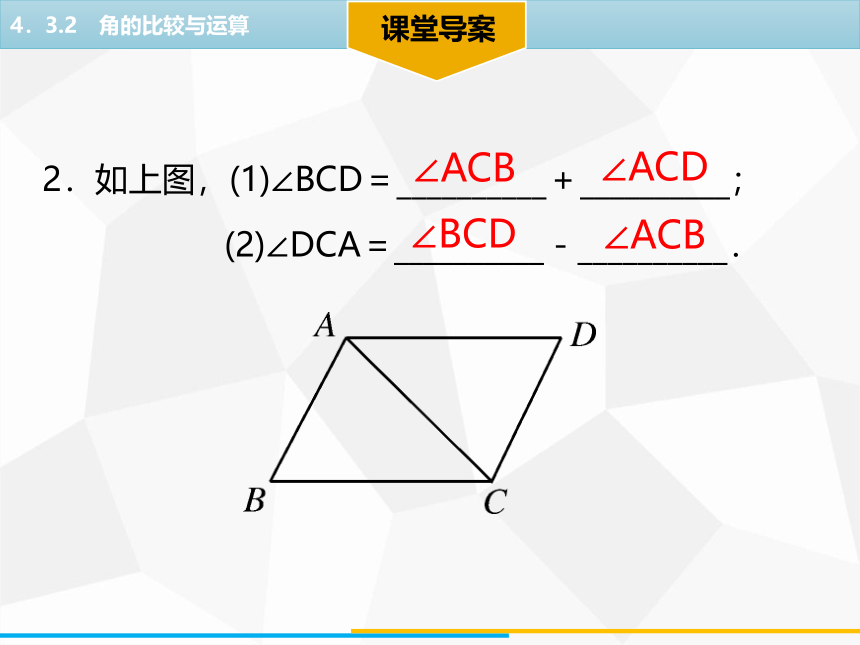
2.如上图,(1)∠BCD=__________+__________;
(2)∠DCA=__________-__________.
∠ACB
∠BCD
∠ACD
∠ACB
课堂导案
知识点2:角平分线的应用及角的综合计算
【例2】如右图所示,∠ABC=80°,
80°,∠CBD=30°,BE平
分∠ABD.求∠CBE的度数.
【答案】解:∵∠ABC=80°,∠CBD=30°,
∠ABD=∠ABC+∠CBD=110°.
∵BE是∠ABD的平分线,
∴∠EBD= ∠ABD=55°,
∴∠CBE=∠EBD-∠CBD=25°.
1
2
课堂导案
【点拔】本题考查了角度的计算,正确理解题目中的角的关系是关键.
【解析】首先求得∠ABD的度数,然后根据角平分线的定义求得∠EBD的度数,然后根据∠CBE=∠EBD-∠CBD求解.
课堂导案
对点训练二
3.如下图,OC平分∠AOB,
OD平分∠BOC,∠AOB=
120°,则∠COD=______度.
30
4.如上图,OD平分∠AOB,
∠BOD=40°,∠AOC=10°,
则∠COD=________度.
30
课堂导案
5.如下图,OC是∠AOD的平分线,∠AOD=110°,∠BOC=35°,求∠AOB的度数.
?
∵OC是∠AOD的平分线,∠AOD=100°,
∴∠AOC= ∠AOD=55°,
∠AOB=∠AOC-∠BOC=20°
1
2
课堂导案
6.如下图,已知∠BOC=2
∠AOC,OD平分∠AOB,
且∠AOC=40°,求∠COD
的度数.
∵∠BOC=2∠AOC,∠AOC=40°,
∴∠BOC=2×40°=80°,
∴∠AOB=∠BOC+∠AOC=80°+40°=120°,∵OD平分∠AOB,∴∠AOD= ∠AOB=60°,
∴∠COD=∠AOD-∠AOC=60°-40°=20°.
1
2
课后练案
7.如下图,已知OB是∠AOC的角平分线,OD是∠COE的角平分线,
(1)若∠BOE=110°,∠AOB
=30°,求∠COE的度数;
?
∵∠AOB=30°,OB是∠AOC的角平分线, ∠BOE=110°,∴∠BOC=∠AOB=30°,∴∠COE=∠BOE-∠BOC=110°-30°=80°;
课后练案
7.如下图,已知OB是∠AOC的角平分线,OD是∠COE的角平分线,
(2)若∠AOE=140°,∠AOC
=60°,求∠DOE的度数.
?
∵∠AOE=140°,∠AOC=60°,
∴∠EOC=∠AOE-∠AOC=140°-60°=80°,∵OD是∠COE的角平分线,
∴∠DOE= ∠COE=40°.
1
2
课后练案
8.如下图所示 , OC是∠AOD的平分线 , OE是∠BOD的平分线.
(1)若∠AOB=120°,则∠COE是多少度?
∵OC是∠AOD的平分线,
∴∠DOC= ∠AOD,
∵OE是∠BOD的平分线,∴∠DOE= ∠BOD,
∴∠COE=∠COD+∠DOE= ∠AOD+ ∠BOD
= (∠AOD+∠BOD)= ∠AOB=60°;
1
2
1
2
1
2
1
2
1
2
1
2
课后练案
8.如下图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
(2)若∠EOC=65°,∠DOC=25°,
则∠BOE是多少度?
∵∠EOC=65°,∠DOC=25°,
∴∠DOE=∠COE-∠DOC=65°-25°=40°,∵OE是∠BOD的平分线,∴∠BOE=∠DOE=40°.
课后练案
9.如下图,已知A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠COE.
(1)若∠AOB=35°,求∠DOE;?
?
OB平分∠AOC,
∴∠AOC=2∠AOB=70°,
∴∠COE=110°
∵OD平分∠COE,∴∠DOE= ∠COE=55°;
1
2
课后练案
9.如下图,已知A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠COE.
(2)试求∠BOD的度数.
?
?
∵OB平分∠AOC,
OD平分∠COE,
∴∠COB= ∠AOC,∠COD= ∠COE,
∴∠BOD=∠COB+∠COD= (∠AOC+∠COE)=90°.
1
2
1
2
1
2
课后练案
10.如下图,O为直线AB上一点,∠AOC=58°,OD平分∠AOC,∠DOE=90°.
(1)求出∠BOD的度数;
∵∠AOC=58°,OD平分∠AOC,
∴∠AOD=29°,∴∠BOD=180°-29°=151°.
课后练案
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
OE是∠BOC的平分线.理由如下:
∵∠AOC=58°,∴∠BOC=122°.
∵OD平分∠AOC,∴∠DOC= ∠AOC=29°.
∵∠DOE=90°,∴∠COE=∠DOE-∠DOC=61°,
∴∠COE= ∠BOC,即OE是∠BOC的平分线.
1
2
1
2
能力培优
11.如下图,已知:∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小;
∵∠AOB是直角,∠AOC=40°,
∴∠AOB=∠AOC=90°=40°=130°,
∵OM是∠BOC的平分线,ON是∠AOC的平分线,∴∠MOC= ∠BOC=65°,∠NOC= ∠AOC=20°
∴∠MON=∠MOC-∠NOC=65°-20°=45°,
1
2
1
2
能力培优
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.
∵∠MON=∠MOC-∠NOC= ∠BOC- ∠AOC
= (∠BOC-∠AOC)= ∠AOB
又∠AOB是直角,不改变,
∴∠MON= ∠AOB=45°.
1
2
1
2
1
2
1
2
1
2
感谢聆听
?
第四章
4.3.2 角的比较与运算
核心目标
……………..…
2
1
课前学案
……………..…
3
课堂导案
……………..…
4
5
课后练案
……………..…
能力培优
……………..…
核心目标
进会比较角的大小,认识角的平分线,会根据几何图形进行角的和、差、倍、分等运算.
课前学案
1.如下图,比较大小:
∠AOB_______∠AOC,∠AOB_______∠BOC.
>
>
课前学案
2.根据图形填空:
(1)∠AOC=∠AOB-______________;
(2)∠AOB=_____________+______________.
3.如上图,OC是∠AOB的平分线,则:
(1)∠AOC=∠_________;(2)∠BOC= _________;
(3)∠AOB=2____________=2_____________.
1
2
∠BOC
BOC
∠AOB
∠AOC
∠BOC
∠AOC
∠BOC
课堂导案
知识点1:角的和差与大小比较
【例1】如右图,用“>”“<”或“=”填空:
?
(1)∠AOD__________∠AOC+∠COD;
(2)∠AOD__________∠AOC;
(3)∠AOB__________∠AOC+∠BOC.
=
>
=
课堂导案
【答案】(1)= (2)> (3)=
【解析】由图形中的角的关系易得出结果.
【点拔】充分利用图形中角的和差关系来确定角的大小数量关系.
课堂导案
对点训练一
1.填上适当的角:
(1)∠BOD=____________+_____________;
(2)∠AOB=∠AOD-_____________;
(3)∠BOC=∠AOC-_____________.
∠BOC
∠BOD
∠COD
∠AOB
课堂导案
2.如上图,(1)∠BCD=__________+__________;
(2)∠DCA=__________-__________.
∠ACB
∠BCD
∠ACD
∠ACB
课堂导案
知识点2:角平分线的应用及角的综合计算
【例2】如右图所示,∠ABC=80°,
80°,∠CBD=30°,BE平
分∠ABD.求∠CBE的度数.
【答案】解:∵∠ABC=80°,∠CBD=30°,
∠ABD=∠ABC+∠CBD=110°.
∵BE是∠ABD的平分线,
∴∠EBD= ∠ABD=55°,
∴∠CBE=∠EBD-∠CBD=25°.
1
2
课堂导案
【点拔】本题考查了角度的计算,正确理解题目中的角的关系是关键.
【解析】首先求得∠ABD的度数,然后根据角平分线的定义求得∠EBD的度数,然后根据∠CBE=∠EBD-∠CBD求解.
课堂导案
对点训练二
3.如下图,OC平分∠AOB,
OD平分∠BOC,∠AOB=
120°,则∠COD=______度.
30
4.如上图,OD平分∠AOB,
∠BOD=40°,∠AOC=10°,
则∠COD=________度.
30
课堂导案
5.如下图,OC是∠AOD的平分线,∠AOD=110°,∠BOC=35°,求∠AOB的度数.
?
∵OC是∠AOD的平分线,∠AOD=100°,
∴∠AOC= ∠AOD=55°,
∠AOB=∠AOC-∠BOC=20°
1
2
课堂导案
6.如下图,已知∠BOC=2
∠AOC,OD平分∠AOB,
且∠AOC=40°,求∠COD
的度数.
∵∠BOC=2∠AOC,∠AOC=40°,
∴∠BOC=2×40°=80°,
∴∠AOB=∠BOC+∠AOC=80°+40°=120°,∵OD平分∠AOB,∴∠AOD= ∠AOB=60°,
∴∠COD=∠AOD-∠AOC=60°-40°=20°.
1
2
课后练案
7.如下图,已知OB是∠AOC的角平分线,OD是∠COE的角平分线,
(1)若∠BOE=110°,∠AOB
=30°,求∠COE的度数;
?
∵∠AOB=30°,OB是∠AOC的角平分线, ∠BOE=110°,∴∠BOC=∠AOB=30°,∴∠COE=∠BOE-∠BOC=110°-30°=80°;
课后练案
7.如下图,已知OB是∠AOC的角平分线,OD是∠COE的角平分线,
(2)若∠AOE=140°,∠AOC
=60°,求∠DOE的度数.
?
∵∠AOE=140°,∠AOC=60°,
∴∠EOC=∠AOE-∠AOC=140°-60°=80°,∵OD是∠COE的角平分线,
∴∠DOE= ∠COE=40°.
1
2
课后练案
8.如下图所示 , OC是∠AOD的平分线 , OE是∠BOD的平分线.
(1)若∠AOB=120°,则∠COE是多少度?
∵OC是∠AOD的平分线,
∴∠DOC= ∠AOD,
∵OE是∠BOD的平分线,∴∠DOE= ∠BOD,
∴∠COE=∠COD+∠DOE= ∠AOD+ ∠BOD
= (∠AOD+∠BOD)= ∠AOB=60°;
1
2
1
2
1
2
1
2
1
2
1
2
课后练案
8.如下图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
(2)若∠EOC=65°,∠DOC=25°,
则∠BOE是多少度?
∵∠EOC=65°,∠DOC=25°,
∴∠DOE=∠COE-∠DOC=65°-25°=40°,∵OE是∠BOD的平分线,∴∠BOE=∠DOE=40°.
课后练案
9.如下图,已知A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠COE.
(1)若∠AOB=35°,求∠DOE;?
?
OB平分∠AOC,
∴∠AOC=2∠AOB=70°,
∴∠COE=110°
∵OD平分∠COE,∴∠DOE= ∠COE=55°;
1
2
课后练案
9.如下图,已知A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠COE.
(2)试求∠BOD的度数.
?
?
∵OB平分∠AOC,
OD平分∠COE,
∴∠COB= ∠AOC,∠COD= ∠COE,
∴∠BOD=∠COB+∠COD= (∠AOC+∠COE)=90°.
1
2
1
2
1
2
课后练案
10.如下图,O为直线AB上一点,∠AOC=58°,OD平分∠AOC,∠DOE=90°.
(1)求出∠BOD的度数;
∵∠AOC=58°,OD平分∠AOC,
∴∠AOD=29°,∴∠BOD=180°-29°=151°.
课后练案
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
OE是∠BOC的平分线.理由如下:
∵∠AOC=58°,∴∠BOC=122°.
∵OD平分∠AOC,∴∠DOC= ∠AOC=29°.
∵∠DOE=90°,∴∠COE=∠DOE-∠DOC=61°,
∴∠COE= ∠BOC,即OE是∠BOC的平分线.
1
2
1
2
能力培优
11.如下图,已知:∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小;
∵∠AOB是直角,∠AOC=40°,
∴∠AOB=∠AOC=90°=40°=130°,
∵OM是∠BOC的平分线,ON是∠AOC的平分线,∴∠MOC= ∠BOC=65°,∠NOC= ∠AOC=20°
∴∠MON=∠MOC-∠NOC=65°-20°=45°,
1
2
1
2
能力培优
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.
∵∠MON=∠MOC-∠NOC= ∠BOC- ∠AOC
= (∠BOC-∠AOC)= ∠AOB
又∠AOB是直角,不改变,
∴∠MON= ∠AOB=45°.
1
2
1
2
1
2
1
2
1
2
感谢聆听
