人教版七上数学周周卷(九): 4.1-4.2直线、射线、线段 习题课件(28张PPT)
文档属性
| 名称 | 人教版七上数学周周卷(九): 4.1-4.2直线、射线、线段 习题课件(28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 00:00:00 | ||
图片预览





文档简介
周周卷(九) 几何图形及直线、射线、线段
测试范围:4.1~4.2
选择题
填空题
解答题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
一、选择题(每小题3分,共30分)
1.下面几种几何图形中,属于平面图形的是( )
①三角形;②长方形;③正方体;④圆;⑤四棱锥;⑥圆柱.
A.①②④ B.①②③ C.①②⑥ D.④⑤⑥
A
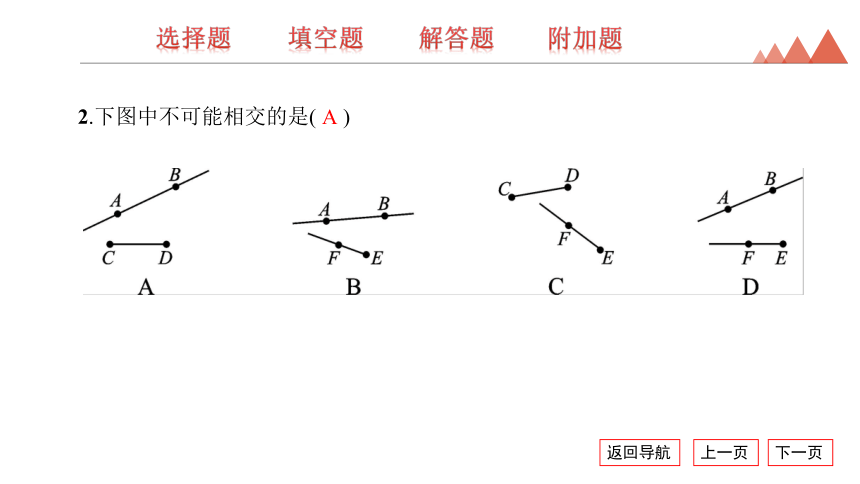
2.下图中不可能相交的是( )
A
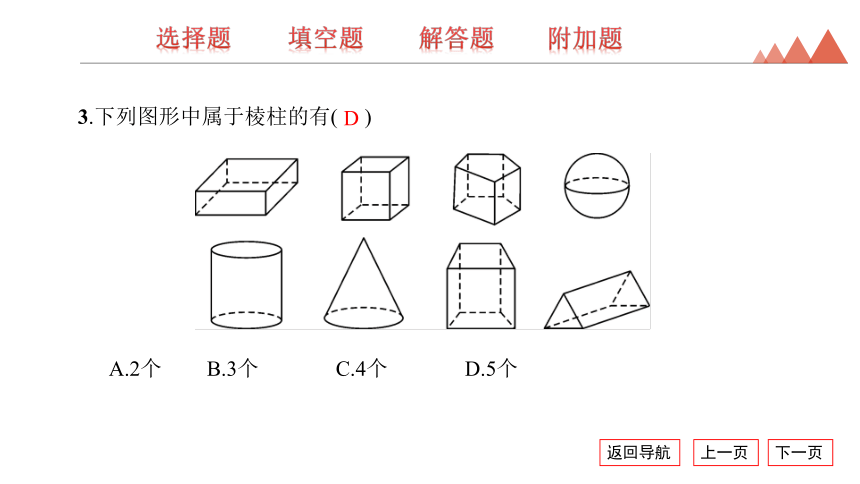
3.下列图形中属于棱柱的有( )
A.2个 B.3个 C.4个 D.5个
D
4.以下给出的几何体中,从正面看是圆的是( )
C
5.植树时,为了使同一行树坑在一条直线上,只需定出两个树坑的位置,其中蕴含的数学原理是( )
A.两点之间,线段最短 B.两点之间,直线最短
C.两点确定一条射线 D.两点确定一条直线
6.下列数学语言中,不正确的是( )
A.画直线MN,在直线MN上任取一点P
B.以点M为端点画射线MA
C.直线a,b相交于点m
D.延长线段MN到点P,使NP=MN
D
C
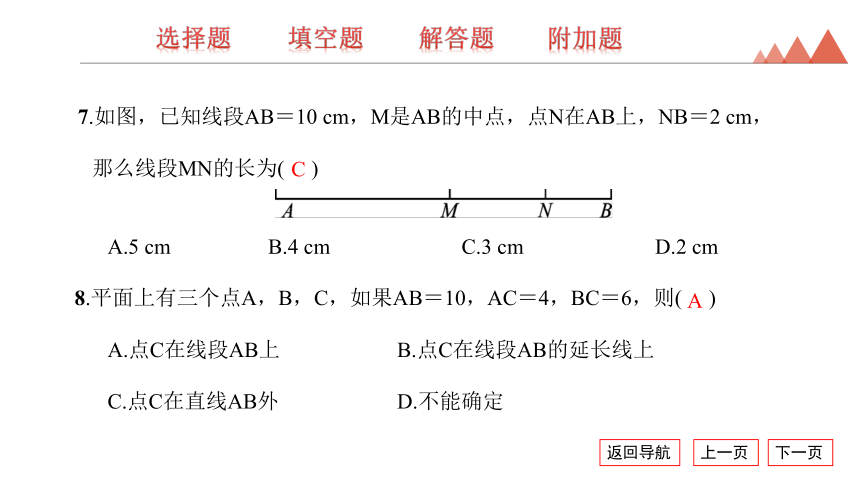
7.如图,已知线段AB=10 cm,M是AB的中点,点N在AB上,NB=2 cm,那么线段MN的长为( )
A.5 cm B.4 cm C.3 cm D.2 cm
8.平面上有三个点A,B,C,如果AB=10,AC=4,BC=6,则( )
A.点C在线段AB上 B.点C在线段AB的延长线上
C.点C在直线AB外 D.不能确定
C
A
9.由绵阳出发到成都的某次列车,运行途中停靠的车站依次是:绵阳→罗江→黄许→德阳→广汉→清白江→新都→成都.那么要为这次列车制作的车票一共有( )
A.7种 B.8种 C.56种 D.28种
D
10.如图是一个正方体,线段AB,BC,CA是它的三个面的对角线,下列图形中是该正方体的表面展开图的是( )
C
二、填空题(每小题3分,共24分)
11.修路时,通常把弯曲的公路改直,这样可以缩短路程,其蕴涵的数学道理是____________________________.
12.根据图中几何体的平面展开图,填写几何体的名称.
(1)____________________,(2)_______,(3)_______.
两点之间,线段最短
长方体(或四棱柱)
圆锥
圆柱
13.如图,可以用字母表示的直线有_______条;可以用字母表示的线段有_______条;在直线EF上的射线有_______条.
第13题图 第14题图
14.看图填空:如图,直线上有四点A,B,C,D,AC=_______+BC;CD=AD-_______;AC+BD-BC=_______.
3
6
6
AB
AC
AD
15.某正方体的平面展开图如图所示,由此可知,原正方体“中”字所在面的对面的汉字是_______.
第15题图 第16题图
16.如图,AB=24,C为AB的中点,点D在线段AC上,且AD= CB,则DB的长度为_______.
的
20
17.已知点A,B,C在同一条直线上,AB=10 cm,AC=8 cm,M,N分别是AB,AC的中点,那么线段MN的长度为_______cm.
18.某公司员工分别住在A,B,C三个住宅区,A区有30人,B区有15人,C区有10人,三个住宅区在一直线上,各住宅区之间的距离如图所示.公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在_______区.
1或9
A
解析:当停靠点在A区时,所有员工步行到停靠点的路程和是15×100+10×300=4500(m);当停靠点在B区时,所有员工步行到停靠点的路程和是30×100+10×200=5000(m);当停靠点在C区时,所有员工步行到停靠点的路程和是30×300+15×200=12000(m),因为4500<5000<12000,所以当停靠点在A区时,所有员工步行到停靠点的路程和最小.
三、解答题(共66分)
19.(8分)如图,第一排中的图形绕虚线旋转一周,能形成第二排中的某个几何体,请你把第一排与第二排中相应的图用线连接起来.
解:如图所示.
20.(8分)如图,已知A,B,C,D四点,根据下列语句画图:
(1)画直线AB;
(2)连接AC,BD,相交于点O;
(3)画射线AD,BC,交于点P.
解:(1)如图所示,直线AB即为所求.
(2)如图所示,线段AC,BD即为所求.
(3)如图所示,射线AD,BC即为所求.
21.(8分)如图,若图中平面展开图折叠成正方体后,相对面上的两个数字之和为5,求x+y+z的值.
解:由题意可知,与x相对的是-1,
所以-1+x=5,解得x=6.与y相对的是8,
所以8+y=5,解得y=-3.与2z相对的是3,
所以3+2z=5,解得z=1,
所以x+y+z=6+(-3)+1=4.
22.(10分)如图,已知线段AB,a,b.
(1)请用尺规按下列要求作图:(不要求写作法,但要保留作图痕迹)
①延长线段AB到点C,使BC=a;
②反向延长线段AB到点D,使AD=b;
解:(1)①如图所示,线段BC即为所求.
②如图所示,线段AD即为所求.
(2)在(1)的条件下,如果AB=8 cm,a=6 cm,b=10 cm,且E为CD的中点,求线段AE的长度.
(2)因为AB=8 cm,a=6 cm,b=10 cm,所以CD=8+6+10=24(cm).
因为E为CD的中点,所以DE= DC=12 cm,
所以AE=DE-AD=12-10=2(cm).
23.(10分)如图,已知线段AB上有两点C,D且AC∶CD∶DB=2∶3∶4,E,F分别为线段AC,DB的中点,EF=3.6 cm.求AB的长.
解:设AC=2x cm,则CD=3x cm,DB=4x cm.
因为E,F分别是线段AC,DB的中点,
所以EC= AC=x cm,DF= DB=2x cm.
因为EF=EC+CD+DF,
所以x+3x+2x=3.6,解得x=0.6,
所以AB=9x=9×0.6=5.4(cm).
24.(10分)用若干个相同的小立方体搭成的几何体,从正面看到的图形和从上面看到的图形如图所示,问这样的几何体有几种可能?它最多需要几个小立方体?最少需要几个小立方体?画出最多、最少时从左面看到的图形.(答案不唯一时,画出一种即可)
解:共有3种可能,最多需要8个小立方体,最少需要7个小立方体.最多时从左边看到的图形如图1所示,最少时从左面看到的图形如图2或如图3所示.
25.(12分)(1)如图,已知点C在线段AB上,AC=6 cm,且BC=4 cm,M,N分别是AC,BC的中点,求线段MN的长度;
解:(1)因为AC=6 cm,M是AC的中点,所以CM= AC=3 cm.
因为BC=4 cm,N是BC的中点,所以CN= BC=2 cm,
所以MN=CM+CN=5 cm,所以线段MN的长度为5 cm.
(2)在(1)题中,如果AC=a cm,BC=b cm,其他条件不变,求MN的长度.请你用一句简洁的话表达你发现的规律;
(2)因为M,N分别是AC,BC的中点,
所以CM= AC,CN= BC,
所以MN= (AC+BC)= cm.
规律:直线上相邻两线段中点间的距离为两线段长度和的一半
(3)对于(1)题,当点C在BA的延长线上时,且AB=m cm,其他条件不变,求MN的长度.
(3)如图,当点C在BA的延长线上时,MN=CN-CM= (BC-AC)= AB= cm.
附加题(10分)
观察图形找出规律,并解答下列问题:
(1)5条直线相交,有_______个交点,平面被分成_______块;
10
16
(2)n条直线相交,有__________个交点,平面被分成____________块;
(3)一张圆饼切10刀(不许重叠),最多可得到多少块饼?
解:(3)将圆饼切10刀,即n=10,最多可得饼 =56(块).
测试范围:4.1~4.2
选择题
填空题
解答题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
一、选择题(每小题3分,共30分)
1.下面几种几何图形中,属于平面图形的是( )
①三角形;②长方形;③正方体;④圆;⑤四棱锥;⑥圆柱.
A.①②④ B.①②③ C.①②⑥ D.④⑤⑥
A
2.下图中不可能相交的是( )
A
3.下列图形中属于棱柱的有( )
A.2个 B.3个 C.4个 D.5个
D
4.以下给出的几何体中,从正面看是圆的是( )
C
5.植树时,为了使同一行树坑在一条直线上,只需定出两个树坑的位置,其中蕴含的数学原理是( )
A.两点之间,线段最短 B.两点之间,直线最短
C.两点确定一条射线 D.两点确定一条直线
6.下列数学语言中,不正确的是( )
A.画直线MN,在直线MN上任取一点P
B.以点M为端点画射线MA
C.直线a,b相交于点m
D.延长线段MN到点P,使NP=MN
D
C
7.如图,已知线段AB=10 cm,M是AB的中点,点N在AB上,NB=2 cm,那么线段MN的长为( )
A.5 cm B.4 cm C.3 cm D.2 cm
8.平面上有三个点A,B,C,如果AB=10,AC=4,BC=6,则( )
A.点C在线段AB上 B.点C在线段AB的延长线上
C.点C在直线AB外 D.不能确定
C
A
9.由绵阳出发到成都的某次列车,运行途中停靠的车站依次是:绵阳→罗江→黄许→德阳→广汉→清白江→新都→成都.那么要为这次列车制作的车票一共有( )
A.7种 B.8种 C.56种 D.28种
D
10.如图是一个正方体,线段AB,BC,CA是它的三个面的对角线,下列图形中是该正方体的表面展开图的是( )
C
二、填空题(每小题3分,共24分)
11.修路时,通常把弯曲的公路改直,这样可以缩短路程,其蕴涵的数学道理是____________________________.
12.根据图中几何体的平面展开图,填写几何体的名称.
(1)____________________,(2)_______,(3)_______.
两点之间,线段最短
长方体(或四棱柱)
圆锥
圆柱
13.如图,可以用字母表示的直线有_______条;可以用字母表示的线段有_______条;在直线EF上的射线有_______条.
第13题图 第14题图
14.看图填空:如图,直线上有四点A,B,C,D,AC=_______+BC;CD=AD-_______;AC+BD-BC=_______.
3
6
6
AB
AC
AD
15.某正方体的平面展开图如图所示,由此可知,原正方体“中”字所在面的对面的汉字是_______.
第15题图 第16题图
16.如图,AB=24,C为AB的中点,点D在线段AC上,且AD= CB,则DB的长度为_______.
的
20
17.已知点A,B,C在同一条直线上,AB=10 cm,AC=8 cm,M,N分别是AB,AC的中点,那么线段MN的长度为_______cm.
18.某公司员工分别住在A,B,C三个住宅区,A区有30人,B区有15人,C区有10人,三个住宅区在一直线上,各住宅区之间的距离如图所示.公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在_______区.
1或9
A
解析:当停靠点在A区时,所有员工步行到停靠点的路程和是15×100+10×300=4500(m);当停靠点在B区时,所有员工步行到停靠点的路程和是30×100+10×200=5000(m);当停靠点在C区时,所有员工步行到停靠点的路程和是30×300+15×200=12000(m),因为4500<5000<12000,所以当停靠点在A区时,所有员工步行到停靠点的路程和最小.
三、解答题(共66分)
19.(8分)如图,第一排中的图形绕虚线旋转一周,能形成第二排中的某个几何体,请你把第一排与第二排中相应的图用线连接起来.
解:如图所示.
20.(8分)如图,已知A,B,C,D四点,根据下列语句画图:
(1)画直线AB;
(2)连接AC,BD,相交于点O;
(3)画射线AD,BC,交于点P.
解:(1)如图所示,直线AB即为所求.
(2)如图所示,线段AC,BD即为所求.
(3)如图所示,射线AD,BC即为所求.
21.(8分)如图,若图中平面展开图折叠成正方体后,相对面上的两个数字之和为5,求x+y+z的值.
解:由题意可知,与x相对的是-1,
所以-1+x=5,解得x=6.与y相对的是8,
所以8+y=5,解得y=-3.与2z相对的是3,
所以3+2z=5,解得z=1,
所以x+y+z=6+(-3)+1=4.
22.(10分)如图,已知线段AB,a,b.
(1)请用尺规按下列要求作图:(不要求写作法,但要保留作图痕迹)
①延长线段AB到点C,使BC=a;
②反向延长线段AB到点D,使AD=b;
解:(1)①如图所示,线段BC即为所求.
②如图所示,线段AD即为所求.
(2)在(1)的条件下,如果AB=8 cm,a=6 cm,b=10 cm,且E为CD的中点,求线段AE的长度.
(2)因为AB=8 cm,a=6 cm,b=10 cm,所以CD=8+6+10=24(cm).
因为E为CD的中点,所以DE= DC=12 cm,
所以AE=DE-AD=12-10=2(cm).
23.(10分)如图,已知线段AB上有两点C,D且AC∶CD∶DB=2∶3∶4,E,F分别为线段AC,DB的中点,EF=3.6 cm.求AB的长.
解:设AC=2x cm,则CD=3x cm,DB=4x cm.
因为E,F分别是线段AC,DB的中点,
所以EC= AC=x cm,DF= DB=2x cm.
因为EF=EC+CD+DF,
所以x+3x+2x=3.6,解得x=0.6,
所以AB=9x=9×0.6=5.4(cm).
24.(10分)用若干个相同的小立方体搭成的几何体,从正面看到的图形和从上面看到的图形如图所示,问这样的几何体有几种可能?它最多需要几个小立方体?最少需要几个小立方体?画出最多、最少时从左面看到的图形.(答案不唯一时,画出一种即可)
解:共有3种可能,最多需要8个小立方体,最少需要7个小立方体.最多时从左边看到的图形如图1所示,最少时从左面看到的图形如图2或如图3所示.
25.(12分)(1)如图,已知点C在线段AB上,AC=6 cm,且BC=4 cm,M,N分别是AC,BC的中点,求线段MN的长度;
解:(1)因为AC=6 cm,M是AC的中点,所以CM= AC=3 cm.
因为BC=4 cm,N是BC的中点,所以CN= BC=2 cm,
所以MN=CM+CN=5 cm,所以线段MN的长度为5 cm.
(2)在(1)题中,如果AC=a cm,BC=b cm,其他条件不变,求MN的长度.请你用一句简洁的话表达你发现的规律;
(2)因为M,N分别是AC,BC的中点,
所以CM= AC,CN= BC,
所以MN= (AC+BC)= cm.
规律:直线上相邻两线段中点间的距离为两线段长度和的一半
(3)对于(1)题,当点C在BA的延长线上时,且AB=m cm,其他条件不变,求MN的长度.
(3)如图,当点C在BA的延长线上时,MN=CN-CM= (BC-AC)= AB= cm.
附加题(10分)
观察图形找出规律,并解答下列问题:
(1)5条直线相交,有_______个交点,平面被分成_______块;
10
16
(2)n条直线相交,有__________个交点,平面被分成____________块;
(3)一张圆饼切10刀(不许重叠),最多可得到多少块饼?
解:(3)将圆饼切10刀,即n=10,最多可得饼 =56(块).
