人教版七上数学周周卷(六):2.2 整式的加减 习题课件(27张PPT)
文档属性
| 名称 | 人教版七上数学周周卷(六):2.2 整式的加减 习题课件(27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 19:10:31 | ||
图片预览







文档简介
周周卷(六) 整式的加减
测试范围:2.2
选择题
填空题
解答题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
一、选择题(每小题3分,共30分)
1.计算2a-3a,结果正确的是( )
A.-1 B.1 C.-a D.a
2.下列各式中,与3x2y3是同类项的是( )
A.2x5 B.3x3y2 C.- x2y3 D.- y5
C
C
3.下列计算正确的是( )
A.3a+2b=5ab B.2ab-ba=ab
C.5y2-2y2=3 D.3x2y-5xy2=2x2y
4.下列去括号正确的是( )
A.3(x+8)=3x+8
B.-(5x-3y)-(2x-y)=-5x+3y-2x+y
C.y-2(x-1)=y-2x-2
D.3(2x-1)-2(x-1)=6x-3-2x-2
B
B
5.若 x3yn+1与-3xm-1y5是同类项,则( )
A.m=4,n=4 B.m=2,n=4
C.m=-4,n=4 D.m=4,n=-4
6.已知M=x2+2xy+y2,N=x2-2xy+y2,则M-N等于( )
A.4xy B.-4xy C.2y2 D.4xy+2y2
A
A
7.如果a2-ab=8,ab+b2=2,那么a2+b2的值是( )
A.10 B.6 C.-6 D.-10
8.已知A=2x2+3mx-x,B=-x2+mx+1,其中m为常数,若A+2B的值与x的取值无关,则m的值为( )
A.0 B.5 C. D.-
A
C
9.某学校七年级学生有m人,八年级人数比七年级人数的 多10人,九年级人数比八年级人数的2倍少50人,用含m的式子表示七、八、九三个年级的总人数为( )
A.3m B. m-40 C.3m-40 D.3m-20
D
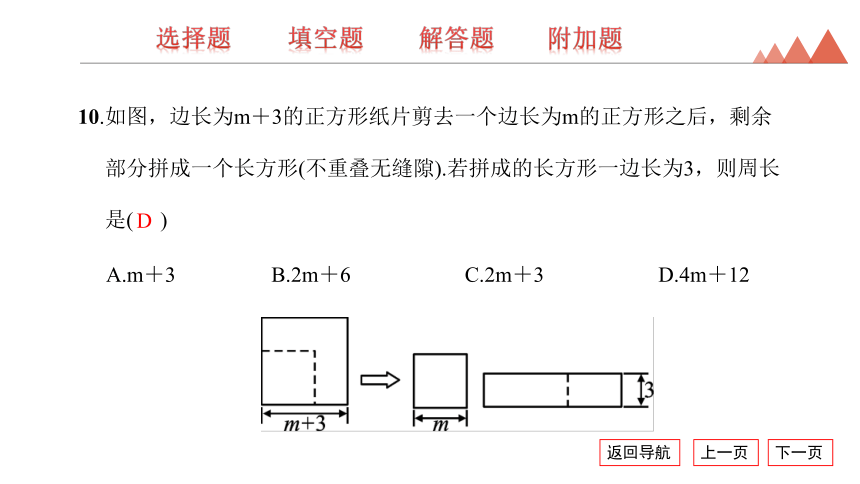
10.如图,边长为m+3的正方形纸片剪去一个边长为m的正方形之后,剩余部分拼成一个长方形(不重叠无缝隙).若拼成的长方形一边长为3,则周长是( )
A.m+3 B.2m+6 C.2m+3 D.4m+12
D
二、填空题(每小题3分,共24分)
11.计算3a-2(a-b)的结果是_______.
12.把x+y看作是一个整体,合并同类项:5(x+y)-(x+y)-3(x+y)=_______.
13.若-3xay3与5x2yb的和仍为单项式,则这两个单项式的和为_______.
14.如图,阴影部分的面积是_______.
a+2b
x+y
2x2y3
15.已知多项式A=x2+2y2,B=-4x2+3y2,且A+B+C=0,则C为____________.
16.若多项式4x3+2x2-(kx2+17x-6)中不含x2的项,则k的值为______________.
17.已知a-b=2,d-b=-2,则(a-d)2的值为_______.
3x2-5y2
2
16
18.如图1所示的是从长方形中剪掉一个较小的长方形,使得剩余两端的宽度相等,用5个这样的图形紧密地拼成如图2所示的图形,则它的长为______________.(用含m,n的式子表示)
m+4n
解析:由图可得,用5个这样的图形紧密地拼成如图2所示的图形,则它的长为3m+2[n-(m-n)]=3m+2(n-m+n)=3m+4n-2m=m+4n.
三、解答题(共66分)
19.(8分)化简下列各式:
(1)3a-2x+6a+3x; (2)5an+(-2an)-8an+1+6an-an+1.
解:(1)原式=(3+6)a+(-2+3)x=9a+x.
(2)原式=(5-2+6)an+(-8-1)an+1=9an-9an+1.
20.(8分)已知 +|y+3|=0,求多项式3(x2-2xy)-[3x2-2y-2(xy+y)-17]的值.
解:因为 +|y+3|=0,
所以x+ =0,y+3=0,所以x=- ,y=-3.
原式=3x2-6xy-(3x2-2y-2xy-2y-17)=3x2-6xy-(3x2-4y-2xy-17)=3x2-6xy-3x2+4y+2xy+17=-4xy+4y+17.
当x=- ,y=-3时,
原式=-4× ×(-3)+4×(-3)+17=-6-12+17=-1.
21.(8分)若关于x,y的多项式mx3+nxy2-2x3-xy2+y+5中不含三次项,求2m+5n的值.
解:mx3+nxy2-2x3-xy2+y+5=(m-2)x3+(n-1)xy2+y+5,
因为多项式中不含三次项,
所以m-2=0,n-1=0,
解得m=2,n=1,则2m+5n=4+5=9.
22.(10分)有理数a,b,c在数轴上对应点的位置如图所示.
(1)填空:a+b_______0,b-1_______0,a-c_______0,1-c_______0;(填“>”“<”或“=”)
<
<
<
>
(2)计算:|a+b|-|b-1|-|a-c|-|1-c|.
(2)|a+b|-|b-1|-|a-c|-|1-c|=(-a-b)-(1-b)-(c-a)-(1-c)=-a-b-1+b-c+a-1+c=-2.
23.(10分)甲、乙、丙三位同学给希望工程捐款.已知甲同学捐款x元,乙同学的捐款金额比甲同学捐款金额的3倍少8元,丙同学的捐款金额是甲、乙两同学捐款总金额的 ,用含x的式子表示甲、乙、丙三位同学的捐款总金额.
解:由题意,可得乙同学捐款(3x-8)元,丙同学的捐款金额是 (x+3x-8)=(3x-6)(元),
故甲、乙、丙三位同学的捐款总金额为x+3x-8+3x-6=(7x-14)(元).答:甲、乙、丙三位同学的捐款总金额为(7x-14)元.
24.(10分)已知A=3a2b-2ab2+abc,小明错将“C=2A-B”看成“C=2A+B”,算得C=4a2b-3ab2+4abc.
(1)求正确的结果;
解:(1)因为2A+B=C,所以B=C-2A=4a2b-3ab2+4abc-2(3a2b-2ab2+abc)=4a2b-3ab2+4abc-6a2b+4ab2-2abc=-2a2b+ab2+2abc,所以2A-B=2(3a2b-2ab2+abc)-(-2a2b+ab2+2abc)=6a2b-4ab2+2abc+2a2b-ab2-2abc=8a2b-5ab2.
(2)小芳说(1)中的结果与c的取值无关,对吗?若a=2,b= ,求(1)中式子的值.
(2)小芳说的对,与c无关.将a=2,b= 代入,得8a2b-5ab2=8×22×
-5×2× =6.
25.(12分)某市居民使用自来水按如下标准收费(水费按月缴纳):
(1)当a=2时,某用户一个月用了18 m3水,求该用户这个月应缴纳的水费;
每月用水量
价格
不超过12 m3的部分
a元/m3
超过12 m3但不超过20 m3的部分
1.5a元/m3
超过20 m3的部分
2a元/m3
解:(1)2×12+2×1.5×(18-12)=42(元).
答:该用户这个月应缴纳42元水费.
(2)设某户某月用水量为n m3,当n>20时,求该用户应缴纳的水费;(用含a,n的整式表示)
(2)a×12+1.5a×8+2a×(n-20)=12a+12a+2na-40a=(2na-16a)(元).答:该用户应缴纳的水费为(2na-16a)元.
(3)当a=2时,甲、乙两用户一个月共用水40 m3.已知甲用户用水量超过了28 m3.设甲用户这个月用水x m3,试求甲、乙两用户这个月共缴纳的水费.(用含x的整式表示)
(3)因为甲、乙两用户一个月共用水40 m3,甲用户用水量超过了28 m3,
所以乙用户用水量不超过12 m3,所以甲用户缴纳的水费为2×12+3×8+4×(x-20)=24+24+4x-80=(4x-32)(元),乙用户缴纳的水费为2×(40-x)=(80-2x)(元),所以甲、乙两用户这个月共缴纳的水费为4x-32+80-2x=(2x+48)(元).答:甲、乙两用户这个月共缴纳的水费为(2x+48)元.
附加题(10分)
将连续偶数2,4,6,…排成如下表格,用十字框框出5个数,解答下列问题:
(1)十字框框出的5个数分别与框中间的数32有什么关系?
解:(1)十字框框出的5个数,上面的数比中间的数32小12,下面的数比中间的数32大12,左边的数比中间的数32小2,右边的数比中间的数32大2,中间的数等于32.
(2)5个数的和与32有什么关系?
(2)因为5个数的和为20+30+32+34+44=160,160=32×5,
所以5个数的和是32的5倍.
(3)如果将十字框上下左右移动,仍框住5个数,这5个数仍有这种规律吗?请通过计算说明.
(3)仍有这种规律.设中间的数为a,则十字框框住的5个数的和为(a-12)+(a-2)+a+(a+2)+(a+12)=5a.因为5a÷5=a,其中a为偶数,所以这5个数的和仍是中间的数的5倍.
测试范围:2.2
选择题
填空题
解答题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
一、选择题(每小题3分,共30分)
1.计算2a-3a,结果正确的是( )
A.-1 B.1 C.-a D.a
2.下列各式中,与3x2y3是同类项的是( )
A.2x5 B.3x3y2 C.- x2y3 D.- y5
C
C
3.下列计算正确的是( )
A.3a+2b=5ab B.2ab-ba=ab
C.5y2-2y2=3 D.3x2y-5xy2=2x2y
4.下列去括号正确的是( )
A.3(x+8)=3x+8
B.-(5x-3y)-(2x-y)=-5x+3y-2x+y
C.y-2(x-1)=y-2x-2
D.3(2x-1)-2(x-1)=6x-3-2x-2
B
B
5.若 x3yn+1与-3xm-1y5是同类项,则( )
A.m=4,n=4 B.m=2,n=4
C.m=-4,n=4 D.m=4,n=-4
6.已知M=x2+2xy+y2,N=x2-2xy+y2,则M-N等于( )
A.4xy B.-4xy C.2y2 D.4xy+2y2
A
A
7.如果a2-ab=8,ab+b2=2,那么a2+b2的值是( )
A.10 B.6 C.-6 D.-10
8.已知A=2x2+3mx-x,B=-x2+mx+1,其中m为常数,若A+2B的值与x的取值无关,则m的值为( )
A.0 B.5 C. D.-
A
C
9.某学校七年级学生有m人,八年级人数比七年级人数的 多10人,九年级人数比八年级人数的2倍少50人,用含m的式子表示七、八、九三个年级的总人数为( )
A.3m B. m-40 C.3m-40 D.3m-20
D
10.如图,边长为m+3的正方形纸片剪去一个边长为m的正方形之后,剩余部分拼成一个长方形(不重叠无缝隙).若拼成的长方形一边长为3,则周长是( )
A.m+3 B.2m+6 C.2m+3 D.4m+12
D
二、填空题(每小题3分,共24分)
11.计算3a-2(a-b)的结果是_______.
12.把x+y看作是一个整体,合并同类项:5(x+y)-(x+y)-3(x+y)=_______.
13.若-3xay3与5x2yb的和仍为单项式,则这两个单项式的和为_______.
14.如图,阴影部分的面积是_______.
a+2b
x+y
2x2y3
15.已知多项式A=x2+2y2,B=-4x2+3y2,且A+B+C=0,则C为____________.
16.若多项式4x3+2x2-(kx2+17x-6)中不含x2的项,则k的值为______________.
17.已知a-b=2,d-b=-2,则(a-d)2的值为_______.
3x2-5y2
2
16
18.如图1所示的是从长方形中剪掉一个较小的长方形,使得剩余两端的宽度相等,用5个这样的图形紧密地拼成如图2所示的图形,则它的长为______________.(用含m,n的式子表示)
m+4n
解析:由图可得,用5个这样的图形紧密地拼成如图2所示的图形,则它的长为3m+2[n-(m-n)]=3m+2(n-m+n)=3m+4n-2m=m+4n.
三、解答题(共66分)
19.(8分)化简下列各式:
(1)3a-2x+6a+3x; (2)5an+(-2an)-8an+1+6an-an+1.
解:(1)原式=(3+6)a+(-2+3)x=9a+x.
(2)原式=(5-2+6)an+(-8-1)an+1=9an-9an+1.
20.(8分)已知 +|y+3|=0,求多项式3(x2-2xy)-[3x2-2y-2(xy+y)-17]的值.
解:因为 +|y+3|=0,
所以x+ =0,y+3=0,所以x=- ,y=-3.
原式=3x2-6xy-(3x2-2y-2xy-2y-17)=3x2-6xy-(3x2-4y-2xy-17)=3x2-6xy-3x2+4y+2xy+17=-4xy+4y+17.
当x=- ,y=-3时,
原式=-4× ×(-3)+4×(-3)+17=-6-12+17=-1.
21.(8分)若关于x,y的多项式mx3+nxy2-2x3-xy2+y+5中不含三次项,求2m+5n的值.
解:mx3+nxy2-2x3-xy2+y+5=(m-2)x3+(n-1)xy2+y+5,
因为多项式中不含三次项,
所以m-2=0,n-1=0,
解得m=2,n=1,则2m+5n=4+5=9.
22.(10分)有理数a,b,c在数轴上对应点的位置如图所示.
(1)填空:a+b_______0,b-1_______0,a-c_______0,1-c_______0;(填“>”“<”或“=”)
<
<
<
>
(2)计算:|a+b|-|b-1|-|a-c|-|1-c|.
(2)|a+b|-|b-1|-|a-c|-|1-c|=(-a-b)-(1-b)-(c-a)-(1-c)=-a-b-1+b-c+a-1+c=-2.
23.(10分)甲、乙、丙三位同学给希望工程捐款.已知甲同学捐款x元,乙同学的捐款金额比甲同学捐款金额的3倍少8元,丙同学的捐款金额是甲、乙两同学捐款总金额的 ,用含x的式子表示甲、乙、丙三位同学的捐款总金额.
解:由题意,可得乙同学捐款(3x-8)元,丙同学的捐款金额是 (x+3x-8)=(3x-6)(元),
故甲、乙、丙三位同学的捐款总金额为x+3x-8+3x-6=(7x-14)(元).答:甲、乙、丙三位同学的捐款总金额为(7x-14)元.
24.(10分)已知A=3a2b-2ab2+abc,小明错将“C=2A-B”看成“C=2A+B”,算得C=4a2b-3ab2+4abc.
(1)求正确的结果;
解:(1)因为2A+B=C,所以B=C-2A=4a2b-3ab2+4abc-2(3a2b-2ab2+abc)=4a2b-3ab2+4abc-6a2b+4ab2-2abc=-2a2b+ab2+2abc,所以2A-B=2(3a2b-2ab2+abc)-(-2a2b+ab2+2abc)=6a2b-4ab2+2abc+2a2b-ab2-2abc=8a2b-5ab2.
(2)小芳说(1)中的结果与c的取值无关,对吗?若a=2,b= ,求(1)中式子的值.
(2)小芳说的对,与c无关.将a=2,b= 代入,得8a2b-5ab2=8×22×
-5×2× =6.
25.(12分)某市居民使用自来水按如下标准收费(水费按月缴纳):
(1)当a=2时,某用户一个月用了18 m3水,求该用户这个月应缴纳的水费;
每月用水量
价格
不超过12 m3的部分
a元/m3
超过12 m3但不超过20 m3的部分
1.5a元/m3
超过20 m3的部分
2a元/m3
解:(1)2×12+2×1.5×(18-12)=42(元).
答:该用户这个月应缴纳42元水费.
(2)设某户某月用水量为n m3,当n>20时,求该用户应缴纳的水费;(用含a,n的整式表示)
(2)a×12+1.5a×8+2a×(n-20)=12a+12a+2na-40a=(2na-16a)(元).答:该用户应缴纳的水费为(2na-16a)元.
(3)当a=2时,甲、乙两用户一个月共用水40 m3.已知甲用户用水量超过了28 m3.设甲用户这个月用水x m3,试求甲、乙两用户这个月共缴纳的水费.(用含x的整式表示)
(3)因为甲、乙两用户一个月共用水40 m3,甲用户用水量超过了28 m3,
所以乙用户用水量不超过12 m3,所以甲用户缴纳的水费为2×12+3×8+4×(x-20)=24+24+4x-80=(4x-32)(元),乙用户缴纳的水费为2×(40-x)=(80-2x)(元),所以甲、乙两用户这个月共缴纳的水费为4x-32+80-2x=(2x+48)(元).答:甲、乙两用户这个月共缴纳的水费为(2x+48)元.
附加题(10分)
将连续偶数2,4,6,…排成如下表格,用十字框框出5个数,解答下列问题:
(1)十字框框出的5个数分别与框中间的数32有什么关系?
解:(1)十字框框出的5个数,上面的数比中间的数32小12,下面的数比中间的数32大12,左边的数比中间的数32小2,右边的数比中间的数32大2,中间的数等于32.
(2)5个数的和与32有什么关系?
(2)因为5个数的和为20+30+32+34+44=160,160=32×5,
所以5个数的和是32的5倍.
(3)如果将十字框上下左右移动,仍框住5个数,这5个数仍有这种规律吗?请通过计算说明.
(3)仍有这种规律.设中间的数为a,则十字框框住的5个数的和为(a-12)+(a-2)+a+(a+2)+(a+12)=5a.因为5a÷5=a,其中a为偶数,所以这5个数的和仍是中间的数的5倍.
