人教版七上数学周周卷(十):4.3 角 习题课件(29张PPT)
文档属性
| 名称 | 人教版七上数学周周卷(十):4.3 角 习题课件(29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 19:14:11 | ||
图片预览

文档简介
周周卷(十) 角
测试范围:4.3
选择题
填空题
解答题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
一、选择题(每小题3分,共30分)
1.已知∠A=55°,则它的补角是( )
A.35° B.55° C.115° D.125°
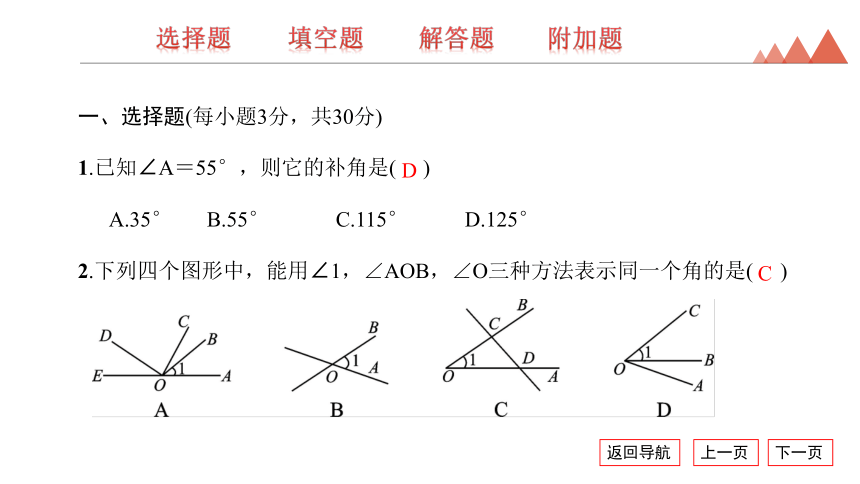
2.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
D
C
3.下列角度换算错误的是( )
A.10.6°=10°36″ B.900″=0.25°
C.1.5°=90′ D.54°16′12″=54.27°
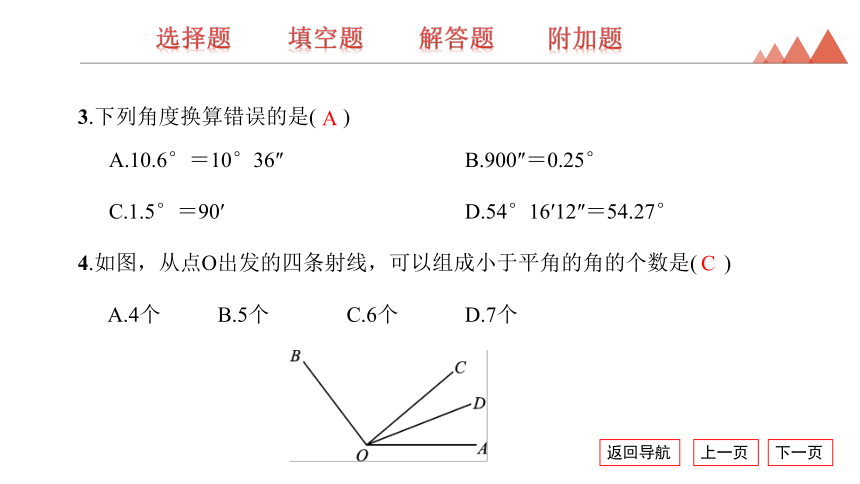
4.如图,从点O出发的四条射线,可以组成小于平角的角的个数是( )
A.4个 B.5个 C.6个 D.7个
A
C
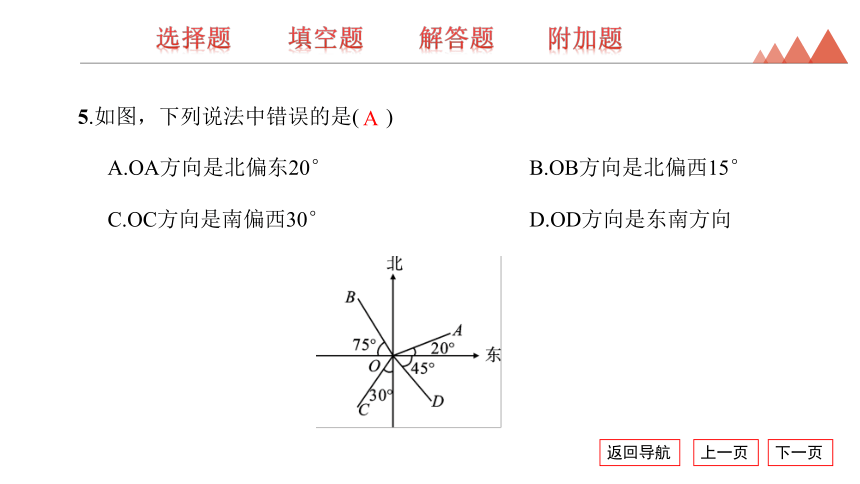
5.如图,下列说法中错误的是( )
A.OA方向是北偏东20° B.OB方向是北偏西15°
C.OC方向是南偏西30° D.OD方向是东南方向
A
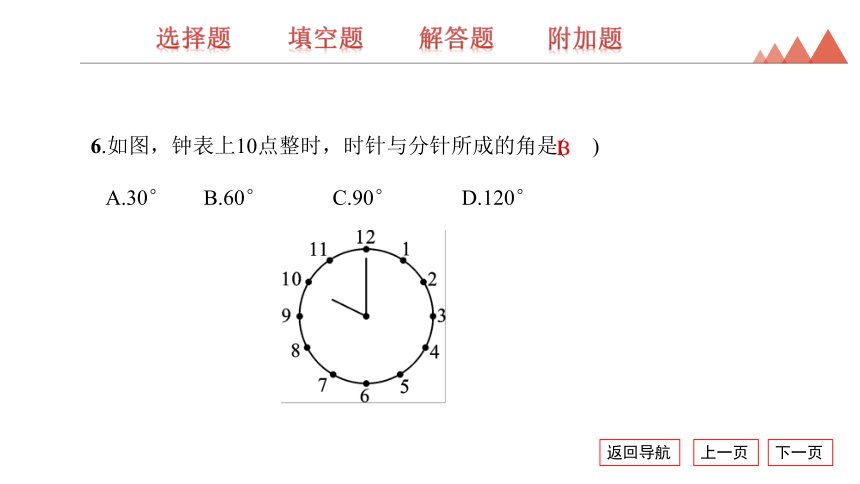
6.如图,钟表上10点整时,时针与分针所成的角是( )
A.30° B.60° C.90° D.120°
B
7.利用三角板工具画角很方便,但是只能画出一些特殊的角,下列角度不能用一副三角板(不再用其他工具)画出的是( )
A.15° B.20° C.75° D.105°
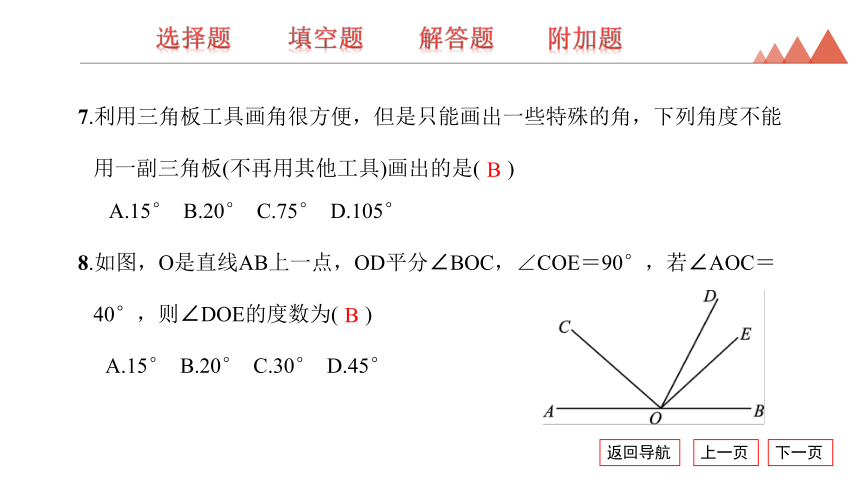
8.如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°,若∠AOC=40°,则∠DOE的度数为( )
A.15° B.20° C.30° D.45°
B
B
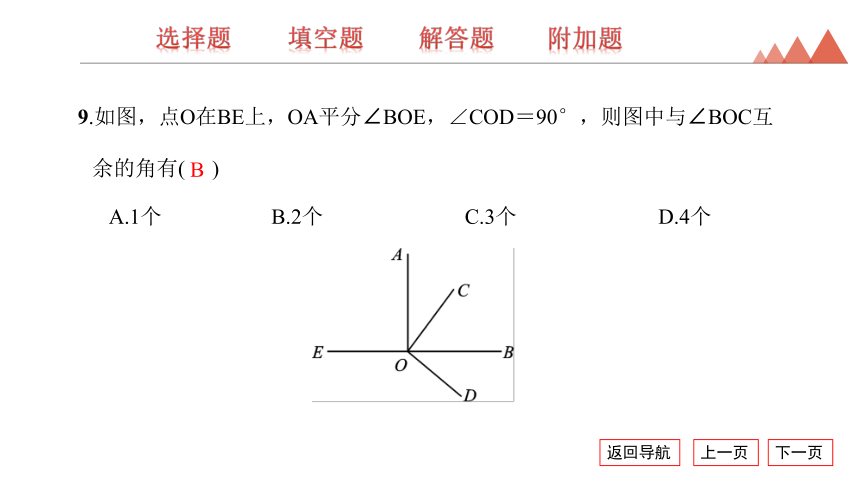
9.如图,点O在BE上,OA平分∠BOE,∠COD=90°,则图中与∠BOC互余的角有( )
A.1个 B.2个 C.3个 D.4个
B
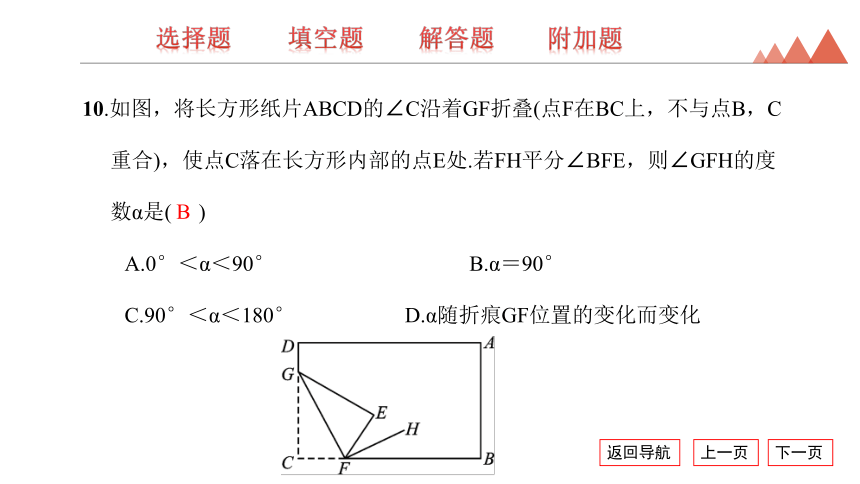
10.如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与点B,C重合),使点C落在长方形内部的点E处.若FH平分∠BFE,则∠GFH的度数α是( )
A.0°<α<90° B.α=90°
C.90°<α<180° D.α随折痕GF位置的变化而变化
B
二、填空题(每小题3分,共24分)
11.如图,∠AOB的大小可由量角器测得,则∠AOB的度数为_______.
12.用“>”“=”或“<”填空:
(1)32.5°_______32°5′;(2)25°12′_______25.2°.
60°
>
=
13.如图,∠AOC=∠COD=∠BOD,则OD平分______________,OC平分______________,∠AOD=______________.
14.一个角的补角比这个角的余角的3倍还大10°,则这个角的余角为_______.
∠BOC
∠AOD
∠BOC
40°
15.如图,点A在点O的北偏西15°方向上,点B在点O的北偏东30°方向上,若∠1=∠AOB,则点C在点O的__________________方向上.
第15题图 第16题图
16.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,若∠1=27°40′,则∠2的度数是_______.
南偏东45°(或东南)
57°40′
17.如图,点A,O,E在同一直线上,∠AOB=40°,∠EOD=28°,OD平分∠COE,则∠COB=_______°.
18.已知∠AOB=3∠BOC,射线OD平分∠AOC,若∠BOD=30°,则∠BOC的度数为___________.
84
15°或30°
解析:当∠BOC在∠AOB内部时,如图1,因为∠AOB=3∠BOC,所以设∠BOC=x,则∠AOB=3x,所以∠AOC=∠AOB-∠BOC=2x.因为OD平分∠AOC,所以∠DOC= ∠AOC=x,所以∠BOD=∠DOC+∠BOC=2x.因为∠BOD=30°,所以2x=30°,所以x=15°,即∠BOC=15°.当∠BOC在∠AOB外部时,如图2,因为∠AOB=3∠BOC,所以设∠BOC=x,则∠AOB=3x,所以∠AOC=∠AOB+∠BOC=4x.因为OD平分∠AOC,所以∠DOC= ∠AOC=2x,所以∠BOD=∠DOC-∠BOC=x.因为∠BOD=30°,所以x=30°,即∠BOC=30°.所以∠BOC的度数为15°或30°.
三、解答题(共66分)
19.(8分)计算:
(1)48°39′+67°31′-21°17′;
(2)23°53′×3-107°43′÷5.
解:(1)48°39′+67°31′-21°17′=116°10′-21°17′=94°53′.
(2)23°53′×3-107°43′÷5=71°39′-21°32′36″=50°6′24″.
20.(8分)已知∠1与∠2互余,且∠1的补角比∠2的2倍多25°,求∠1的大小.
解:设∠1=x°,则∠2=(90-x)°.
根据题意,得180-x=2(90-x)+25,解得x=25,
所以∠1=25°.
21.(8分)如图,∠AOD=120°,∠2=2∠1=60°.
(1)求∠DOC的度数;
(2)求∠BOD的度数.
解:(1)因为∠DOC=∠AOD-∠2,
∠AOD=120°,∠2=60°,
所以∠DOC=120°-60°=60°.
(2)因为∠2=2∠1=60°,所以∠1= ×60°=30°.
因为∠BOD=∠AOD+∠1,所以∠BOD=120°+30°=150°.
22.(10分)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是______________ ;
(2)若射线OE平分∠COD,求∠AOE的度数;
(3)直接写出一对互余的角和一对互补的角.
北偏东70°
解:(2)因为∠AOB=55°,∠AOC=∠AOB,所以∠BOC=110°.
因为射线OD是OB的反向延长线,所以∠BOD=180°,
所以∠COD=180°-110°=70°.
因为OE平分∠COD,所以∠COE=35°.
因为∠AOC=55°,所以∠AOE=∠AOC+∠COE=90°.
(3)答案不唯一,如∠AOC与∠COE互余,∠AOB与∠AOD互补.
23.(10分)如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠BOD的度数.
解:设∠COE=α,则∠BOE=2α,∠BOC=3α.
因为∠FOE=90°,所以∠BOF=90°+2α.
又因为OC平分∠BOF,所以∠BOC= ∠BOF=45°+α,
所以3α=45°+α,解得α=22.5°,
所以∠BOC=67.5°,所以∠BOD=180°-∠BOC=112.5°.
24.(10分)如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,求∠EOF的度数.
解:因为OF平分∠BOC,∠BOC=60°,所以∠COF=30°,所以∠EOF=∠COE-∠COF=∠COE-30°.
因为OE平分∠AOC,所以∠AOC=2∠COE.
又因为∠AOC+∠EOF=156°,
所以2∠COE+∠COE-30°=156°,解得∠COE=62°,
所以∠EOF=62°-30°=32°.
25.(12分)已知∠AOC=∠BOD=α(0°<α<180°).
(1)如图1,若α=90°:
①写出图中一组相等的角(除直角外)_____________________,理由是____________________________;
②试猜想∠COD和∠AOB的数量关系,并说明理由;
∠AOD=∠BOC
同角的余角相等
解:②∠COD和∠AOB互补.理由如下:因为∠AOD=∠BOD-∠AOB=90°-∠AOB,所以∠COD=∠AOD+∠AOC=90°-∠AOB+90°,所以∠AOB+∠COD=180°,所以∠COD和∠AOB互补.
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是___________________________;当α=_______°,
∠COD和∠AOB互余.
∠COD+∠AOB=2∠AOC
45
附加题(10分)
O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图1,当直角三角板MON的一边ON与射线OB重合时,则∠MOC=_______;
25°
(2)如图2,将直角三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线,求旋转角∠BON和∠CON的度数;
解:(2)因为∠BOC=65°,OC是∠MOB的平分线,
所以∠MOB=2∠BOC=130°,
所以∠BON=∠MOB-∠MON=130°-90°=40°,
∠CON=∠COB-∠BON=65°-40°=25°.
(3)因为∠NOC= ∠AOM,所以∠AOM=4∠NOC.
又因为∠BOC=65°,
所以∠AOC=∠AOB-∠BOC=180°-65°=115°.
因为∠MON=90°,
所以∠AOM+∠CON=∠AOC-∠MON=115°-90°=25°,
所以4∠NOC+∠NOC=25°,所以∠NOC=5°,
所以∠NOB=∠NOC+∠BOC=70°.
(3)将直角三角板MON绕点O逆时针旋转至图3所示位置时,∠NOC=
∠AOM,求∠NOB的度数.
测试范围:4.3
选择题
填空题
解答题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
一、选择题(每小题3分,共30分)
1.已知∠A=55°,则它的补角是( )
A.35° B.55° C.115° D.125°
2.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
D
C
3.下列角度换算错误的是( )
A.10.6°=10°36″ B.900″=0.25°
C.1.5°=90′ D.54°16′12″=54.27°
4.如图,从点O出发的四条射线,可以组成小于平角的角的个数是( )
A.4个 B.5个 C.6个 D.7个
A
C
5.如图,下列说法中错误的是( )
A.OA方向是北偏东20° B.OB方向是北偏西15°
C.OC方向是南偏西30° D.OD方向是东南方向
A
6.如图,钟表上10点整时,时针与分针所成的角是( )
A.30° B.60° C.90° D.120°
B
7.利用三角板工具画角很方便,但是只能画出一些特殊的角,下列角度不能用一副三角板(不再用其他工具)画出的是( )
A.15° B.20° C.75° D.105°
8.如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°,若∠AOC=40°,则∠DOE的度数为( )
A.15° B.20° C.30° D.45°
B
B
9.如图,点O在BE上,OA平分∠BOE,∠COD=90°,则图中与∠BOC互余的角有( )
A.1个 B.2个 C.3个 D.4个
B
10.如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与点B,C重合),使点C落在长方形内部的点E处.若FH平分∠BFE,则∠GFH的度数α是( )
A.0°<α<90° B.α=90°
C.90°<α<180° D.α随折痕GF位置的变化而变化
B
二、填空题(每小题3分,共24分)
11.如图,∠AOB的大小可由量角器测得,则∠AOB的度数为_______.
12.用“>”“=”或“<”填空:
(1)32.5°_______32°5′;(2)25°12′_______25.2°.
60°
>
=
13.如图,∠AOC=∠COD=∠BOD,则OD平分______________,OC平分______________,∠AOD=______________.
14.一个角的补角比这个角的余角的3倍还大10°,则这个角的余角为_______.
∠BOC
∠AOD
∠BOC
40°
15.如图,点A在点O的北偏西15°方向上,点B在点O的北偏东30°方向上,若∠1=∠AOB,则点C在点O的__________________方向上.
第15题图 第16题图
16.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,若∠1=27°40′,则∠2的度数是_______.
南偏东45°(或东南)
57°40′
17.如图,点A,O,E在同一直线上,∠AOB=40°,∠EOD=28°,OD平分∠COE,则∠COB=_______°.
18.已知∠AOB=3∠BOC,射线OD平分∠AOC,若∠BOD=30°,则∠BOC的度数为___________.
84
15°或30°
解析:当∠BOC在∠AOB内部时,如图1,因为∠AOB=3∠BOC,所以设∠BOC=x,则∠AOB=3x,所以∠AOC=∠AOB-∠BOC=2x.因为OD平分∠AOC,所以∠DOC= ∠AOC=x,所以∠BOD=∠DOC+∠BOC=2x.因为∠BOD=30°,所以2x=30°,所以x=15°,即∠BOC=15°.当∠BOC在∠AOB外部时,如图2,因为∠AOB=3∠BOC,所以设∠BOC=x,则∠AOB=3x,所以∠AOC=∠AOB+∠BOC=4x.因为OD平分∠AOC,所以∠DOC= ∠AOC=2x,所以∠BOD=∠DOC-∠BOC=x.因为∠BOD=30°,所以x=30°,即∠BOC=30°.所以∠BOC的度数为15°或30°.
三、解答题(共66分)
19.(8分)计算:
(1)48°39′+67°31′-21°17′;
(2)23°53′×3-107°43′÷5.
解:(1)48°39′+67°31′-21°17′=116°10′-21°17′=94°53′.
(2)23°53′×3-107°43′÷5=71°39′-21°32′36″=50°6′24″.
20.(8分)已知∠1与∠2互余,且∠1的补角比∠2的2倍多25°,求∠1的大小.
解:设∠1=x°,则∠2=(90-x)°.
根据题意,得180-x=2(90-x)+25,解得x=25,
所以∠1=25°.
21.(8分)如图,∠AOD=120°,∠2=2∠1=60°.
(1)求∠DOC的度数;
(2)求∠BOD的度数.
解:(1)因为∠DOC=∠AOD-∠2,
∠AOD=120°,∠2=60°,
所以∠DOC=120°-60°=60°.
(2)因为∠2=2∠1=60°,所以∠1= ×60°=30°.
因为∠BOD=∠AOD+∠1,所以∠BOD=120°+30°=150°.
22.(10分)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是______________ ;
(2)若射线OE平分∠COD,求∠AOE的度数;
(3)直接写出一对互余的角和一对互补的角.
北偏东70°
解:(2)因为∠AOB=55°,∠AOC=∠AOB,所以∠BOC=110°.
因为射线OD是OB的反向延长线,所以∠BOD=180°,
所以∠COD=180°-110°=70°.
因为OE平分∠COD,所以∠COE=35°.
因为∠AOC=55°,所以∠AOE=∠AOC+∠COE=90°.
(3)答案不唯一,如∠AOC与∠COE互余,∠AOB与∠AOD互补.
23.(10分)如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠BOD的度数.
解:设∠COE=α,则∠BOE=2α,∠BOC=3α.
因为∠FOE=90°,所以∠BOF=90°+2α.
又因为OC平分∠BOF,所以∠BOC= ∠BOF=45°+α,
所以3α=45°+α,解得α=22.5°,
所以∠BOC=67.5°,所以∠BOD=180°-∠BOC=112.5°.
24.(10分)如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,求∠EOF的度数.
解:因为OF平分∠BOC,∠BOC=60°,所以∠COF=30°,所以∠EOF=∠COE-∠COF=∠COE-30°.
因为OE平分∠AOC,所以∠AOC=2∠COE.
又因为∠AOC+∠EOF=156°,
所以2∠COE+∠COE-30°=156°,解得∠COE=62°,
所以∠EOF=62°-30°=32°.
25.(12分)已知∠AOC=∠BOD=α(0°<α<180°).
(1)如图1,若α=90°:
①写出图中一组相等的角(除直角外)_____________________,理由是____________________________;
②试猜想∠COD和∠AOB的数量关系,并说明理由;
∠AOD=∠BOC
同角的余角相等
解:②∠COD和∠AOB互补.理由如下:因为∠AOD=∠BOD-∠AOB=90°-∠AOB,所以∠COD=∠AOD+∠AOC=90°-∠AOB+90°,所以∠AOB+∠COD=180°,所以∠COD和∠AOB互补.
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是___________________________;当α=_______°,
∠COD和∠AOB互余.
∠COD+∠AOB=2∠AOC
45
附加题(10分)
O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图1,当直角三角板MON的一边ON与射线OB重合时,则∠MOC=_______;
25°
(2)如图2,将直角三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线,求旋转角∠BON和∠CON的度数;
解:(2)因为∠BOC=65°,OC是∠MOB的平分线,
所以∠MOB=2∠BOC=130°,
所以∠BON=∠MOB-∠MON=130°-90°=40°,
∠CON=∠COB-∠BON=65°-40°=25°.
(3)因为∠NOC= ∠AOM,所以∠AOM=4∠NOC.
又因为∠BOC=65°,
所以∠AOC=∠AOB-∠BOC=180°-65°=115°.
因为∠MON=90°,
所以∠AOM+∠CON=∠AOC-∠MON=115°-90°=25°,
所以4∠NOC+∠NOC=25°,所以∠NOC=5°,
所以∠NOB=∠NOC+∠BOC=70°.
(3)将直角三角板MON绕点O逆时针旋转至图3所示位置时,∠NOC=
∠AOM,求∠NOB的度数.
