苏科版八年级数学上册第5章《平面直角坐标系》培优试题 (word版 含答案)
文档属性
| 名称 | 苏科版八年级数学上册第5章《平面直角坐标系》培优试题 (word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 21:29:37 | ||
图片预览



文档简介
第5章《平面直角坐标系》培优试题
一.选择题(共10小题,每小题2分,共20分)
1.笛卡尔是法国著名的数学家,他首先提出并创建了坐标的思想,引入坐标和变量的概念,平面直角坐标系很好地体现了下列哪一种数学思想?
A.数形结合
B.类比
C.分类讨论
D.建模
2.若点在第四象限,且,,则
A.
B.1
C.5
D.
3.已知点在平面直角坐标系的第二象限内,则的取值范围是
A.
B.
C.
D.
4.在某个电影院里,如果用表示2排15号,那么5排9号可以表示为
A.
B.
C.
D.
5.根据下列表述,能确定位置的是
A.天益广场南区
B.凤凰山北偏东
C.红旗影院5排9座
D.学校操场的西面
6.在平面直角坐标系中,点可以由点通过两次平移得到,正确的是
A.先向左平移4个单位长度,再向上平移6个单位长度
B.先向右平移4个单位长度,再向上平移6个单位长度
C.先向左平移4个单位长度,再向下平移6个单位长度
D.先向右平移4个单位长度,再向下平移6个单位长度
7.在平面直角坐标系中,点,,,若轴,则线段的最小值及此时点的坐标分别为
A.6,
B.10,
C.1,
D.3,
8.在平面直角坐标系中,点到原点的距离是
A.1
B.
C.
D.
9.在平面直角坐标系中,点,一定在
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10.若点,关于轴对称,则
A.,
B.,
C.,
D.,
二.填空题(共8小题,每小题3分,共24分)
11.,已知点的坐标为,则点在第
象限,它到轴的距离为
,到轴的距离为
.
12.如图,、两点的坐标分别为,,点是轴上一点,且的面积为6,则点的坐标为
.
13.如图,的顶点的坐标为,的坐标为;把沿轴向右平移得到,如果的坐标为,那么的长为
.
14.已知点在二、四象限的角平分线上,则
.
15.已知平面直角坐标系内不同的两点和到轴的距离相等,则的值为
.
16.已知直角坐标平面内两点和,则、两点间的距离等于
.
17.已知点与点关于坐标原点对称,则
.
18.如图,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点,,,,那么点的坐标为
.
三.解答题(共6小题,满分52分,其中19题6分,20、21每小题8分,22、23、24每小题10分)
19.已知点,.
(1)如果点、关于轴对称,求、的值;
(2)如果点、关于轴对称,求、的值.
20.已知点,解答下列各题:
(1)若点在轴上,则点的坐标为
;
(2)若,且轴,则点的坐标为
;
(3)若点在第二象限,且它到轴、轴的距离相等,求的值.
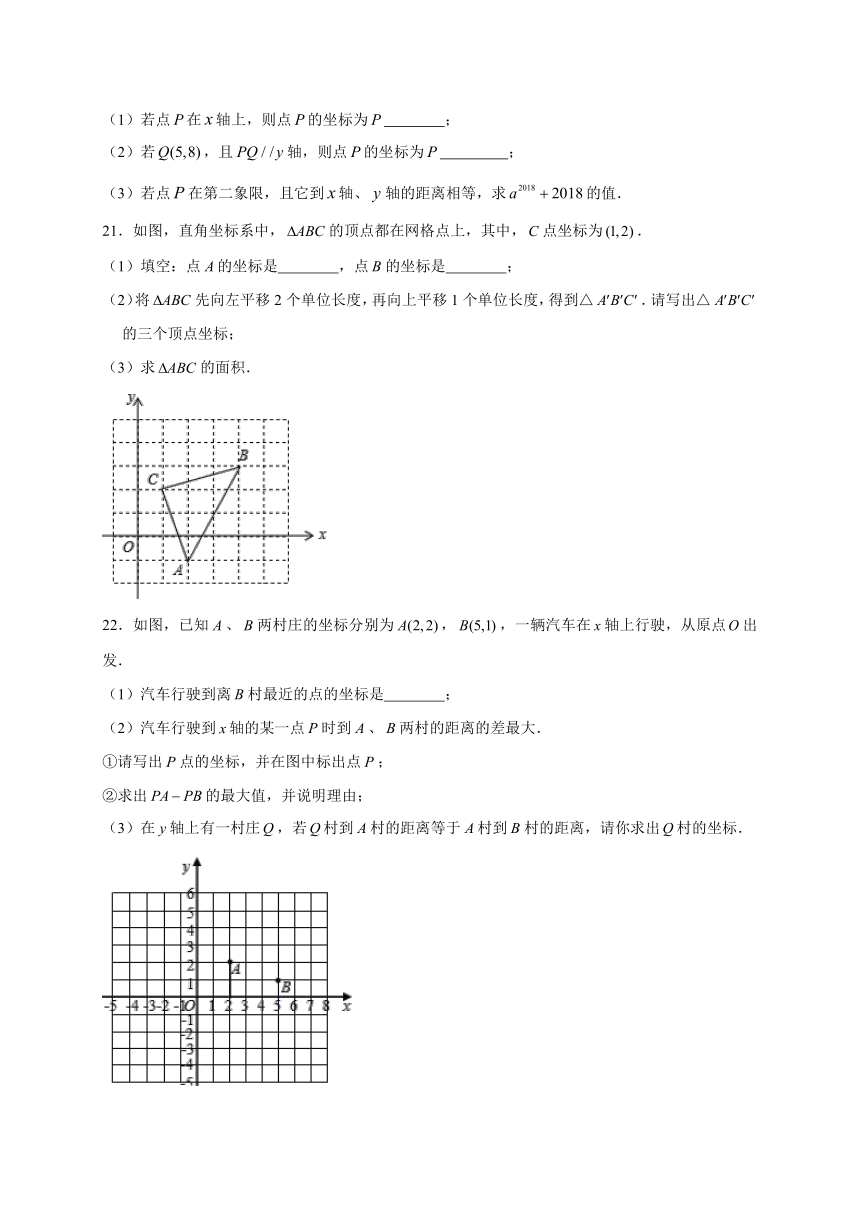
21.如图,直角坐标系中,的顶点都在网格点上,其中,点坐标为.
(1)填空:点的坐标是
,点的坐标是
;
(2)将先向左平移2个单位长度,再向上平移1个单位长度,得到△.请写出△的三个顶点坐标;
(3)求的面积.
22.如图,已知、两村庄的坐标分别为,,一辆汽车在轴上行驶,从原点出发.
(1)汽车行驶到离村最近的点的坐标是
;
(2)汽车行驶到轴的某一点时到、两村的距离的差最大.
①请写出点的坐标,并在图中标出点;
②求出的最大值,并说明理由;
(3)在轴上有一村庄,若村到村的距离等于村到村的距离,请你求出村的坐标.
23.阅读下列一段文字,然后回答问题.
已知在平面内两点,、,,其两点间的距离,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为或.
(1)已知、,则
;
(2)已知轴,点的纵坐标为5,点的纵坐标为,则
.
(3)已知一个三角形各顶点坐标为、、,请判定此三角形的形状,并说明理由.
24.如图,在平面直角坐标系中,点,的坐标分别为,,现同时将点,分别向上平移2个单位,再向右平移1个单位,分别得到点,的对应点,,连接,.
(1)求点,的坐标及四边形的面积;
(2)在轴上是否存在一点,连接,,使?若存在这样一点,求出点的坐标;若不存在,试说明理由.
参考简答
一.选择题(共10小题)
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
二.填空题(共8小题)
11., 二 , 4
,
3
.
12. 或 .
13. 7 .
14. .
15 1或 .
16. .
17. 2 .
18. .
三.解答题(共6小题)
19.已知点,.
(1)如果点、关于轴对称,求、的值;
(2)如果点、关于轴对称,求、的值.
【解】:(1)点、关于轴对称,
,
解得:;
(2)点、关于轴对称,
,
解得:.
20.已知点,解答下列各题:
(1)若点在轴上,则点的坐标为
;
(2)若,且轴,则点的坐标为
;
(3)若点在第二象限,且它到轴、轴的距离相等,求的值.
【解】:(1)由题意可得:,解得:,
,
所以点的坐标为;
(2)根据题意可得:,解得:,
,
所以点的坐标为;
(3)根据题意可得:,
解得:,
把代入,
21.如图,直角坐标系中,的顶点都在网格点上,其中,点坐标为.
(1)填空:点的坐标是
,点的坐标是
;
(2)将先向左平移2个单位长度,再向上平移1个单位长度,得到△.请写出△的三个顶点坐标;
(3)求的面积.
【解】:(1),;
(2)如图,△为所作;,,;
(3)的面积.
22.如图,已知、两村庄的坐标分别为,,一辆汽车在轴上行驶,从原点出发.
(1)汽车行驶到离村最近的点的坐标是
;
(2)汽车行驶到轴的某一点时到、两村的距离的差最大.
①请写出点的坐标,并在图中标出点;
②求出的最大值,并说明理由;
(3)在轴上有一村庄,若村到村的距离等于村到村的距离,请你求出村的坐标.
【解】:(1)由题意,汽车行驶到离村最近的点的坐标是.
(2)①如图,点即为所求.
②,
当点在的延长线上时,的值最大,最大值.
(3)设,,
,
解得或,
或.
23.阅读下列一段文字,然后回答问题.
已知在平面内两点,、,,其两点间的距离,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为或.
(1)已知、,则
;
(2)已知轴,点的纵坐标为5,点的纵坐标为,则
.
(3)已知一个三角形各顶点坐标为、、,请判定此三角形的形状,并说明理由.
【解】:(1)、,
;
(2)、在平行于轴的直线上,点的纵坐标为5,点的纵坐标为,
;
(3)为等腰三角形,理由为:
、、,
,,
,即,
则为等腰三角形;
,
为等腰直角三角形;
24.如图,在平面直角坐标系中,点,的坐标分别为,,现同时将点,分别向上平移2个单位,再向右平移1个单位,分别得到点,的对应点,,连接,.
(1)求点,的坐标及四边形的面积;
(2)在轴上是否存在一点,连接,,使?若存在这样一点,求出点的坐标;若不存在,试说明理由.
【解】:(1)依题意,得,,
;
(2)在轴上是否存在一点,使.理由如下:
设点到的距离为,
,
由,得,
解得,
或.
第13题图
第12题图
一.选择题(共10小题,每小题2分,共20分)
1.笛卡尔是法国著名的数学家,他首先提出并创建了坐标的思想,引入坐标和变量的概念,平面直角坐标系很好地体现了下列哪一种数学思想?
A.数形结合
B.类比
C.分类讨论
D.建模
2.若点在第四象限,且,,则
A.
B.1
C.5
D.
3.已知点在平面直角坐标系的第二象限内,则的取值范围是
A.
B.
C.
D.
4.在某个电影院里,如果用表示2排15号,那么5排9号可以表示为
A.
B.
C.
D.
5.根据下列表述,能确定位置的是
A.天益广场南区
B.凤凰山北偏东
C.红旗影院5排9座
D.学校操场的西面
6.在平面直角坐标系中,点可以由点通过两次平移得到,正确的是
A.先向左平移4个单位长度,再向上平移6个单位长度
B.先向右平移4个单位长度,再向上平移6个单位长度
C.先向左平移4个单位长度,再向下平移6个单位长度
D.先向右平移4个单位长度,再向下平移6个单位长度
7.在平面直角坐标系中,点,,,若轴,则线段的最小值及此时点的坐标分别为
A.6,
B.10,
C.1,
D.3,
8.在平面直角坐标系中,点到原点的距离是
A.1
B.
C.
D.
9.在平面直角坐标系中,点,一定在
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10.若点,关于轴对称,则
A.,
B.,
C.,
D.,
二.填空题(共8小题,每小题3分,共24分)
11.,已知点的坐标为,则点在第
象限,它到轴的距离为
,到轴的距离为
.
12.如图,、两点的坐标分别为,,点是轴上一点,且的面积为6,则点的坐标为
.
13.如图,的顶点的坐标为,的坐标为;把沿轴向右平移得到,如果的坐标为,那么的长为
.
14.已知点在二、四象限的角平分线上,则
.
15.已知平面直角坐标系内不同的两点和到轴的距离相等,则的值为
.
16.已知直角坐标平面内两点和,则、两点间的距离等于
.
17.已知点与点关于坐标原点对称,则
.
18.如图,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点,,,,那么点的坐标为
.
三.解答题(共6小题,满分52分,其中19题6分,20、21每小题8分,22、23、24每小题10分)
19.已知点,.
(1)如果点、关于轴对称,求、的值;
(2)如果点、关于轴对称,求、的值.
20.已知点,解答下列各题:
(1)若点在轴上,则点的坐标为
;
(2)若,且轴,则点的坐标为
;
(3)若点在第二象限,且它到轴、轴的距离相等,求的值.
21.如图,直角坐标系中,的顶点都在网格点上,其中,点坐标为.
(1)填空:点的坐标是
,点的坐标是
;
(2)将先向左平移2个单位长度,再向上平移1个单位长度,得到△.请写出△的三个顶点坐标;
(3)求的面积.
22.如图,已知、两村庄的坐标分别为,,一辆汽车在轴上行驶,从原点出发.
(1)汽车行驶到离村最近的点的坐标是
;
(2)汽车行驶到轴的某一点时到、两村的距离的差最大.
①请写出点的坐标,并在图中标出点;
②求出的最大值,并说明理由;
(3)在轴上有一村庄,若村到村的距离等于村到村的距离,请你求出村的坐标.
23.阅读下列一段文字,然后回答问题.
已知在平面内两点,、,,其两点间的距离,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为或.
(1)已知、,则
;
(2)已知轴,点的纵坐标为5,点的纵坐标为,则
.
(3)已知一个三角形各顶点坐标为、、,请判定此三角形的形状,并说明理由.
24.如图,在平面直角坐标系中,点,的坐标分别为,,现同时将点,分别向上平移2个单位,再向右平移1个单位,分别得到点,的对应点,,连接,.
(1)求点,的坐标及四边形的面积;
(2)在轴上是否存在一点,连接,,使?若存在这样一点,求出点的坐标;若不存在,试说明理由.
参考简答
一.选择题(共10小题)
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
二.填空题(共8小题)
11., 二 , 4
,
3
.
12. 或 .
13. 7 .
14. .
15 1或 .
16. .
17. 2 .
18. .
三.解答题(共6小题)
19.已知点,.
(1)如果点、关于轴对称,求、的值;
(2)如果点、关于轴对称,求、的值.
【解】:(1)点、关于轴对称,
,
解得:;
(2)点、关于轴对称,
,
解得:.
20.已知点,解答下列各题:
(1)若点在轴上,则点的坐标为
;
(2)若,且轴,则点的坐标为
;
(3)若点在第二象限,且它到轴、轴的距离相等,求的值.
【解】:(1)由题意可得:,解得:,
,
所以点的坐标为;
(2)根据题意可得:,解得:,
,
所以点的坐标为;
(3)根据题意可得:,
解得:,
把代入,
21.如图,直角坐标系中,的顶点都在网格点上,其中,点坐标为.
(1)填空:点的坐标是
,点的坐标是
;
(2)将先向左平移2个单位长度,再向上平移1个单位长度,得到△.请写出△的三个顶点坐标;
(3)求的面积.
【解】:(1),;
(2)如图,△为所作;,,;
(3)的面积.
22.如图,已知、两村庄的坐标分别为,,一辆汽车在轴上行驶,从原点出发.
(1)汽车行驶到离村最近的点的坐标是
;
(2)汽车行驶到轴的某一点时到、两村的距离的差最大.
①请写出点的坐标,并在图中标出点;
②求出的最大值,并说明理由;
(3)在轴上有一村庄,若村到村的距离等于村到村的距离,请你求出村的坐标.
【解】:(1)由题意,汽车行驶到离村最近的点的坐标是.
(2)①如图,点即为所求.
②,
当点在的延长线上时,的值最大,最大值.
(3)设,,
,
解得或,
或.
23.阅读下列一段文字,然后回答问题.
已知在平面内两点,、,,其两点间的距离,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为或.
(1)已知、,则
;
(2)已知轴,点的纵坐标为5,点的纵坐标为,则
.
(3)已知一个三角形各顶点坐标为、、,请判定此三角形的形状,并说明理由.
【解】:(1)、,
;
(2)、在平行于轴的直线上,点的纵坐标为5,点的纵坐标为,
;
(3)为等腰三角形,理由为:
、、,
,,
,即,
则为等腰三角形;
,
为等腰直角三角形;
24.如图,在平面直角坐标系中,点,的坐标分别为,,现同时将点,分别向上平移2个单位,再向右平移1个单位,分别得到点,的对应点,,连接,.
(1)求点,的坐标及四边形的面积;
(2)在轴上是否存在一点,连接,,使?若存在这样一点,求出点的坐标;若不存在,试说明理由.
【解】:(1)依题意,得,,
;
(2)在轴上是否存在一点,使.理由如下:
设点到的距离为,
,
由,得,
解得,
或.
第13题图
第12题图
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
