2020-2021学年苏科新版八年级上册数学《第5章 平面直角坐标系》单元测试卷(word版 含解析)
文档属性
| 名称 | 2020-2021学年苏科新版八年级上册数学《第5章 平面直角坐标系》单元测试卷(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 221.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 21:50:55 | ||
图片预览

文档简介
2020-2021学年苏科新版八年级上册数学《第5章
平面直角坐标系》单元测试卷
一.选择题
1.在平面直角坐标系中,点P(﹣2,﹣6)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知点A与点B关于原点对称,若点A的坐标为(﹣2,3),则点B的坐标是( )
A.(﹣3,2)
B.(﹣2,﹣3)
C.(3,﹣2)
D.(2,﹣3)
3.在平面直角坐标系中,若点M(﹣2,3)与点N(﹣2,y)之间的距离是5,那么y的值是( )
A.﹣2
B.8
C.2或8
D.﹣2或8
4.点P与点Q(3,﹣1)关于y轴对称,则点P的坐标为( )
A.(3,1)
B.(3,﹣1)
C.(﹣3,1)
D.(﹣3,﹣1)
5.已知点A(a,2019)与点A′(﹣2020,b)是关于原点O的对称点,则a+b的值为( )
A.1
B.5
C.6
D.4
6.在平面直角坐标系中,若点M(﹣1,3)与点N(﹣1,a)之间的距离是5,那么a的值是( )
A.﹣2
B.8
C.2或8
D.﹣2或8
7.平面直角坐标中,已知点P(a,3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(﹣a,3)
B.(a,﹣3)
C.(﹣a+2,3)
D.(﹣a+4,3)
8.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系:将原图形( )
A.向上平移3个单位长度
B.向下平移3个单位长度
C.向左平移3个单位长度
D.向右平移3个单位长度
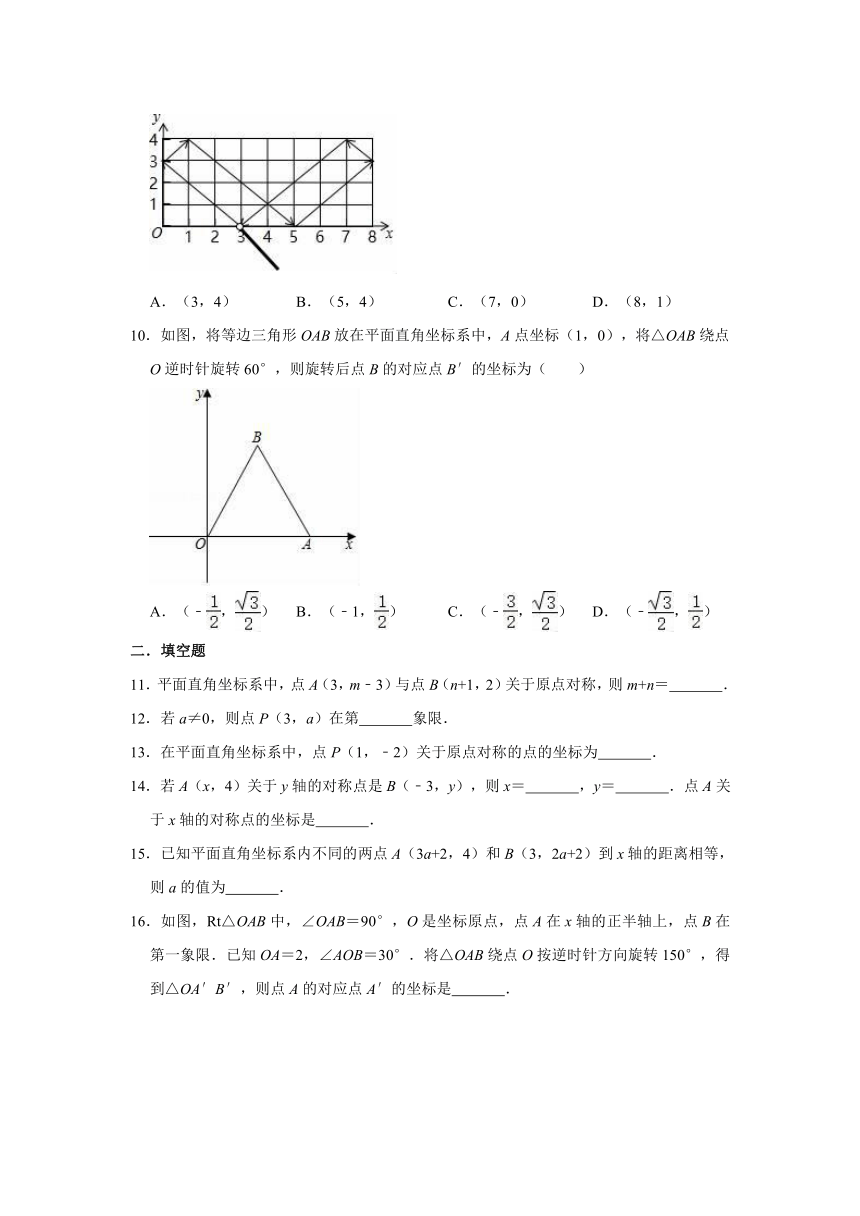
9.如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2020次碰到球桌边时,小球的位置是( )
A.(3,4)
B.(5,4)
C.(7,0)
D.(8,1)
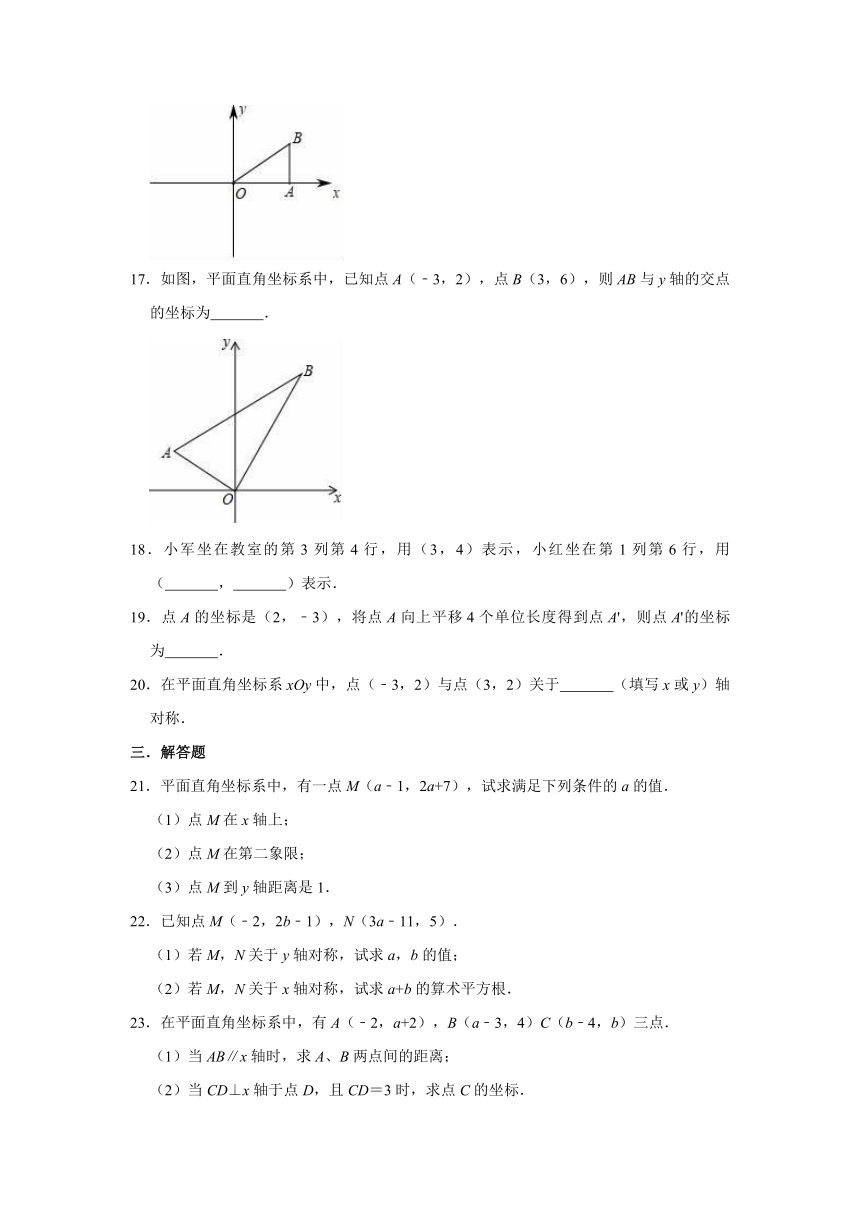
10.如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O逆时针旋转60°,则旋转后点B的对应点B′的坐标为( )
A.(﹣,)
B.(﹣1,)
C.(﹣,)
D.(﹣,)
二.填空题
11.平面直角坐标系中,点A(3,m﹣3)与点B(n+1,2)关于原点对称,则m+n=
.
12.若a≠0,则点P(3,a)在第
象限.
13.在平面直角坐标系中,点P(1,﹣2)关于原点对称的点的坐标为
.
14.若A(x,4)关于y轴的对称点是B(﹣3,y),则x=
,y=
.点A关于x轴的对称点的坐标是
.
15.已知平面直角坐标系内不同的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为
.
16.如图,Rt△OAB中,∠OAB=90°,O是坐标原点,点A在x轴的正半轴上,点B在第一象限.已知OA=2,∠AOB=30°.将△OAB绕点O按逆时针方向旋转150°,得到△OA′B′,则点A的对应点A′的坐标是
.
17.如图,平面直角坐标系中,已知点A(﹣3,2),点B(3,6),则AB与y轴的交点的坐标为
.
18.小军坐在教室的第3列第4行,用(3,4)表示,小红坐在第1列第6行,用(
,
)表示.
19.点A的坐标是(2,﹣3),将点A向上平移4个单位长度得到点A',则点A'的坐标为
.
20.在平面直角坐标系xOy中,点(﹣3,2)与点(3,2)关于
(填写x或y)轴对称.
三.解答题
21.平面直角坐标系中,有一点M(a﹣1,2a+7),试求满足下列条件的a的值.
(1)点M在x轴上;
(2)点M在第二象限;
(3)点M到y轴距离是1.
22.已知点M(﹣2,2b﹣1),N(3a﹣11,5).
(1)若M,N关于y轴对称,试求a,b的值;
(2)若M,N关于x轴对称,试求a+b的算术平方根.
23.在平面直角坐标系中,有A(﹣2,a+2),B(a﹣3,4)C(b﹣4,b)三点.
(1)当AB∥x轴时,求A、B两点间的距离;
(2)当CD⊥x轴于点D,且CD=3时,求点C的坐标.
24.七年级(2)班的同学组织到人民公园游玩,张明、王励、李华三位同学和其他同学走散了,同学们已到中心广场,他们三个对着景区示意图在电话中向在中心广场的同学们说他们的位置,张明说他的坐标是(200,﹣200),王励说他的坐标是(﹣200,﹣100),李华说他的坐标是(﹣300,200).
(1)请你根据题目条件,在图中画出平面直角坐标系;
(2)写出这三位同学所在位置的景点名称;
(3)写出除了这三位同学所在位置外,图中其余两个景点的坐标.
25.如图所示,在边长为1的正方形网格中,△ABC的三个顶点和点D都在小方格的顶点上,请你平移△ABC,使点A平移到点D,得到△DEF.
26.在平面直角坐标系中,点P(2﹣m,3m+6).
(1)若点P与x轴的距离为9,求m的值;
(2)若点P在过点A(2,﹣3)且与y轴平行的直线上,求点P的坐标.
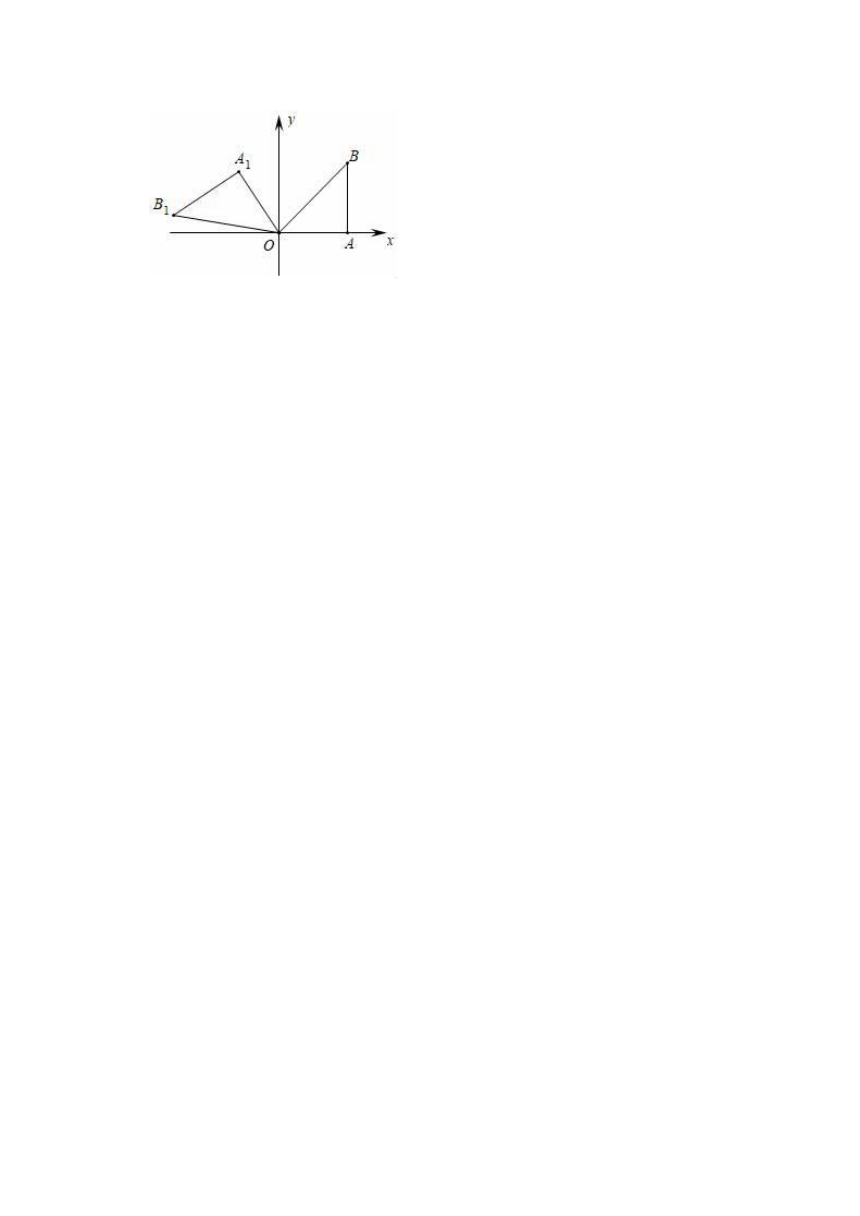
27.如图在平面直角坐标系xOy中,A(6,0),B(6,6),将Rt△OAB绕点O逆时针旋转120°后得到Rt△OA1B1
(1)填空:∠A1OB=
;
(2)求A1的坐标;
(3)求B1的坐标.
参考答案与试题解析
一.选择题
1.解:点P(﹣2,﹣6)所在的象限是第三象限.
故选:C.
2.解:∵点A与点B关于原点对称,点A的坐标为(﹣2,3),
∴点B的坐标是(2,﹣3).
故选:D.
3.解:∵点M(﹣2,3)与点N(﹣2,y)之间的距离是5,
∴|y﹣3|=5,
解得:y=8或y=﹣2.
故选:D.
4.解:∵点P与点Q(3,﹣1)关于y轴对称,
∴点Q的坐标为(﹣3,﹣1).
故选:D.
5.解:∵点A(a,2019)与点A′(﹣2020,b)是关于原点O的对称点,
∴a=2020,b=﹣2019,
∴a+b=1.
故选:A.
6.解:∵点M(﹣1,3)与点N(﹣1,a)的横坐标都是﹣1,
∴MN∥y轴,
点N在点M的上边时,a=3+5=8,
点N在点M的下边时,a=3﹣5=﹣2,
综上所述,a的值是﹣2或8.
故选:D.
7.解:∵直线m上各点的横坐标都是2,
∴直线为:x=2,
∵点P(a,3)在第二象限,
∴a到直线m的距离为:2﹣a,
∴点P关于直线m对称的点的横坐标是:2﹣a+2=4﹣a,
故P点对称的点的坐标是:(﹣a+4,3).
故选:D.
8.解:将△ABC各点的纵坐标保持不变,横坐标都减去3,所得图形与原图形相比向左平移了3个单位.
故选:C.
9.解:由图可得,
点(1,0)第一次碰撞后的点的坐标为(0,1),
第二次碰撞后的点的坐标为(3,4),
第三次碰撞后的点的坐标为(7,0),
第四次碰撞后的点的坐标为(8,1),
第五次碰撞后的点的坐标为(5,4),
第六次碰撞后的点的坐标为(1,0),
…,
∵2020÷6=336…4,
∴小球第2020次碰到球桌边时,小球的位置是(8,1),
故选:D.
10.解:如图,故点B作BH⊥OA于H,设BB′交y轴于J.
∵A(1,0),
∴OA=1,
∵△AOB是等边三角形,BH⊥OA,
∴OH=AH=OA=,BH=OH=,
∴B(,),
∵∠AOB=∠BOB′=60°,∠JOA=90°,
∴∠BOJ=∠JOB′=30°,
∵OB=OB′,
∴BB′⊥OJ,
∴BJ=JB′,
∴B,B′关于y轴对称,
∴B′(﹣,),
故选:A.
二.填空题
11.解:∵点A(3,m﹣3)与点B(n+1,2)关于原点对称,
∴﹣3=n+1,m﹣3=﹣2,
解得:n=﹣4,m=1,
则m+n=﹣4+1=﹣3.
故答案为:﹣3.
12.解:若a≠0,则点P(3,a)在第一或四象限,
故答案为:一或四.
13.解:根据中心对称的性质,可知:点P(1,﹣2)关于原点O中心对称的点的坐标为(﹣1,2).
故答案是:(﹣1,2).
14.解:∵A(x,4)关于y轴的对称点是B(﹣3,y),
∴x=3,y=4,
∴A点坐标为(3,4),
∴点A关于x轴的对称点的坐标是(3,﹣4),
故答案为:3;4;(3,﹣4).
15.解:∵平面直角坐标系内不同的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,
∴|2a+2|=4,
解得:a1=1,a2=﹣3.
故答案为:1或﹣3.
16.解:如图,∵△OA′B′是由△OAB绕点O按逆时针方向旋转150°得到,
∴B′落在x轴的负半轴上,OA′=OA,A′B′=AB,∠A′OB′=∠AOB=30°,
作A′M⊥OB′于M,
∴A′M=OA′==1,OM=OA′=,
∴点A′(﹣,1),
故答案为:(﹣,1).
17.解:设直线AB的解析式为y=kx+b(k≠0),将A(﹣3,2),B(3,6)分别代入得:
,
解得:,
∴y=x+4,
令x=0,得y=4,
∴AB与y轴的交点的坐标为(0,4).
故答案为:(0,4).
18.解:小军坐在教室的第3列第4行,用(3,4)表示,小红坐在第1列第6行,用(
1,6)表示,
故答案为1,6.
19.解:将点A(2,﹣3)向上平移4个单位得到点A′,
则点A′的坐标是(2,﹣3+4),即(2,1).
故答案为(2,1).
20.解:∵点(﹣3,2)与点(3,2)的横坐标互为相反数,纵坐标相同,
∴点(﹣3,2)与点(3,2)关于y轴对称,
故答案为y.
三.解答题
21.解:(1)要使点M在x轴上,a应满足2a+7=0,解得a=,
所以,当a=时,点M在x轴上;
(2)要使点M在第二象限,a应满足,解得,
所以,当时,点M在第二象限;
(3)要使点M到y轴距离是1,a应满足|a﹣1|=±1,解得a=2或a=0,
所以,当a=2或a=0时,点M到y轴距离是1.
22.解:(1)依题意得3a﹣11=2,2b﹣1=5,
∴a=,b=3.
(2)依题意得3a﹣11=﹣2,2b﹣1=﹣5,
∴a=3,b=﹣2,
∴=1.
23.解:(1)∵AB∥x轴,
∴A点和B的纵坐标相等,
即a+2=4,解得a=2,
∴A(﹣2,4),B(﹣1,4),
∴A、B两点间的距离为﹣1﹣(﹣2)=1;
(2)∵当CD⊥x轴于点D,CD=3,
∴|b|=3,解得b=3或b=﹣3,
∴当b=3时,b﹣4=﹣1;当b=﹣3时,b﹣4=﹣7,
∴C点坐标为(﹣1,3)或(﹣7,﹣3).
24.(1)根据题意,他们以中心广场为坐标原点,100m为单位长度建立直角坐标系:
(2)张明在游乐园,王励在望春亭,李华在湖心亭;
(3)中心广场(0,0),牡丹亭(300,300)
25.解:如图所示:
26.解:(1)因为点P(2﹣m,3m+6),点P在x轴的距离为9,
所以|3m+6|=9,
解得m=1或﹣5.
答:m的值为1或﹣5;
(2)因为点P在过点A(2,﹣3)且与y轴平行的直线上,
所以2﹣m=2,
解得m=0,
所以3m+6=6,
所以点P的坐标为(2,6).
27.解:(1)∵A(6,0),B(6,6),
∴△AOB是等腰直角三角形,
∴∠AOB=45°,
∵∠AOA1=120°,
∴∠A1OB=75°,
故答案为75°.
(2)作A1H⊥y轴于H.
∵OA1=6,∠A1OH=30°,
∴A1H=OA1=3,OH=A1H=3,
∴A1(﹣3,3).
(3)作B1K⊥OH于K,在B1K上取一点J,使得OJ=JB1,连接OJ.
由题意OB1=OB=6,设OK=m,则OJ=JB=2m,JK=m,
∵OK2+B1K2=B1O2,
∴m2+(2m+m)2=72,
解得m=3﹣3(负根已经舍弃),
∴KB1=3+3,
∴B1(﹣3﹣3,3﹣3).
平面直角坐标系》单元测试卷
一.选择题
1.在平面直角坐标系中,点P(﹣2,﹣6)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知点A与点B关于原点对称,若点A的坐标为(﹣2,3),则点B的坐标是( )
A.(﹣3,2)
B.(﹣2,﹣3)
C.(3,﹣2)
D.(2,﹣3)
3.在平面直角坐标系中,若点M(﹣2,3)与点N(﹣2,y)之间的距离是5,那么y的值是( )
A.﹣2
B.8
C.2或8
D.﹣2或8
4.点P与点Q(3,﹣1)关于y轴对称,则点P的坐标为( )
A.(3,1)
B.(3,﹣1)
C.(﹣3,1)
D.(﹣3,﹣1)
5.已知点A(a,2019)与点A′(﹣2020,b)是关于原点O的对称点,则a+b的值为( )
A.1
B.5
C.6
D.4
6.在平面直角坐标系中,若点M(﹣1,3)与点N(﹣1,a)之间的距离是5,那么a的值是( )
A.﹣2
B.8
C.2或8
D.﹣2或8
7.平面直角坐标中,已知点P(a,3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(﹣a,3)
B.(a,﹣3)
C.(﹣a+2,3)
D.(﹣a+4,3)
8.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系:将原图形( )
A.向上平移3个单位长度
B.向下平移3个单位长度
C.向左平移3个单位长度
D.向右平移3个单位长度
9.如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2020次碰到球桌边时,小球的位置是( )
A.(3,4)
B.(5,4)
C.(7,0)
D.(8,1)
10.如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O逆时针旋转60°,则旋转后点B的对应点B′的坐标为( )
A.(﹣,)
B.(﹣1,)
C.(﹣,)
D.(﹣,)
二.填空题
11.平面直角坐标系中,点A(3,m﹣3)与点B(n+1,2)关于原点对称,则m+n=
.
12.若a≠0,则点P(3,a)在第
象限.
13.在平面直角坐标系中,点P(1,﹣2)关于原点对称的点的坐标为
.
14.若A(x,4)关于y轴的对称点是B(﹣3,y),则x=
,y=
.点A关于x轴的对称点的坐标是
.
15.已知平面直角坐标系内不同的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为
.
16.如图,Rt△OAB中,∠OAB=90°,O是坐标原点,点A在x轴的正半轴上,点B在第一象限.已知OA=2,∠AOB=30°.将△OAB绕点O按逆时针方向旋转150°,得到△OA′B′,则点A的对应点A′的坐标是
.
17.如图,平面直角坐标系中,已知点A(﹣3,2),点B(3,6),则AB与y轴的交点的坐标为
.
18.小军坐在教室的第3列第4行,用(3,4)表示,小红坐在第1列第6行,用(
,
)表示.
19.点A的坐标是(2,﹣3),将点A向上平移4个单位长度得到点A',则点A'的坐标为
.
20.在平面直角坐标系xOy中,点(﹣3,2)与点(3,2)关于
(填写x或y)轴对称.
三.解答题
21.平面直角坐标系中,有一点M(a﹣1,2a+7),试求满足下列条件的a的值.
(1)点M在x轴上;
(2)点M在第二象限;
(3)点M到y轴距离是1.
22.已知点M(﹣2,2b﹣1),N(3a﹣11,5).
(1)若M,N关于y轴对称,试求a,b的值;
(2)若M,N关于x轴对称,试求a+b的算术平方根.
23.在平面直角坐标系中,有A(﹣2,a+2),B(a﹣3,4)C(b﹣4,b)三点.
(1)当AB∥x轴时,求A、B两点间的距离;
(2)当CD⊥x轴于点D,且CD=3时,求点C的坐标.
24.七年级(2)班的同学组织到人民公园游玩,张明、王励、李华三位同学和其他同学走散了,同学们已到中心广场,他们三个对着景区示意图在电话中向在中心广场的同学们说他们的位置,张明说他的坐标是(200,﹣200),王励说他的坐标是(﹣200,﹣100),李华说他的坐标是(﹣300,200).
(1)请你根据题目条件,在图中画出平面直角坐标系;
(2)写出这三位同学所在位置的景点名称;
(3)写出除了这三位同学所在位置外,图中其余两个景点的坐标.
25.如图所示,在边长为1的正方形网格中,△ABC的三个顶点和点D都在小方格的顶点上,请你平移△ABC,使点A平移到点D,得到△DEF.
26.在平面直角坐标系中,点P(2﹣m,3m+6).
(1)若点P与x轴的距离为9,求m的值;
(2)若点P在过点A(2,﹣3)且与y轴平行的直线上,求点P的坐标.
27.如图在平面直角坐标系xOy中,A(6,0),B(6,6),将Rt△OAB绕点O逆时针旋转120°后得到Rt△OA1B1
(1)填空:∠A1OB=
;
(2)求A1的坐标;
(3)求B1的坐标.
参考答案与试题解析
一.选择题
1.解:点P(﹣2,﹣6)所在的象限是第三象限.
故选:C.
2.解:∵点A与点B关于原点对称,点A的坐标为(﹣2,3),
∴点B的坐标是(2,﹣3).
故选:D.
3.解:∵点M(﹣2,3)与点N(﹣2,y)之间的距离是5,
∴|y﹣3|=5,
解得:y=8或y=﹣2.
故选:D.
4.解:∵点P与点Q(3,﹣1)关于y轴对称,
∴点Q的坐标为(﹣3,﹣1).
故选:D.
5.解:∵点A(a,2019)与点A′(﹣2020,b)是关于原点O的对称点,
∴a=2020,b=﹣2019,
∴a+b=1.
故选:A.
6.解:∵点M(﹣1,3)与点N(﹣1,a)的横坐标都是﹣1,
∴MN∥y轴,
点N在点M的上边时,a=3+5=8,
点N在点M的下边时,a=3﹣5=﹣2,
综上所述,a的值是﹣2或8.
故选:D.
7.解:∵直线m上各点的横坐标都是2,
∴直线为:x=2,
∵点P(a,3)在第二象限,
∴a到直线m的距离为:2﹣a,
∴点P关于直线m对称的点的横坐标是:2﹣a+2=4﹣a,
故P点对称的点的坐标是:(﹣a+4,3).
故选:D.
8.解:将△ABC各点的纵坐标保持不变,横坐标都减去3,所得图形与原图形相比向左平移了3个单位.
故选:C.
9.解:由图可得,
点(1,0)第一次碰撞后的点的坐标为(0,1),
第二次碰撞后的点的坐标为(3,4),
第三次碰撞后的点的坐标为(7,0),
第四次碰撞后的点的坐标为(8,1),
第五次碰撞后的点的坐标为(5,4),
第六次碰撞后的点的坐标为(1,0),
…,
∵2020÷6=336…4,
∴小球第2020次碰到球桌边时,小球的位置是(8,1),
故选:D.
10.解:如图,故点B作BH⊥OA于H,设BB′交y轴于J.
∵A(1,0),
∴OA=1,
∵△AOB是等边三角形,BH⊥OA,
∴OH=AH=OA=,BH=OH=,
∴B(,),
∵∠AOB=∠BOB′=60°,∠JOA=90°,
∴∠BOJ=∠JOB′=30°,
∵OB=OB′,
∴BB′⊥OJ,
∴BJ=JB′,
∴B,B′关于y轴对称,
∴B′(﹣,),
故选:A.
二.填空题
11.解:∵点A(3,m﹣3)与点B(n+1,2)关于原点对称,
∴﹣3=n+1,m﹣3=﹣2,
解得:n=﹣4,m=1,
则m+n=﹣4+1=﹣3.
故答案为:﹣3.
12.解:若a≠0,则点P(3,a)在第一或四象限,
故答案为:一或四.
13.解:根据中心对称的性质,可知:点P(1,﹣2)关于原点O中心对称的点的坐标为(﹣1,2).
故答案是:(﹣1,2).
14.解:∵A(x,4)关于y轴的对称点是B(﹣3,y),
∴x=3,y=4,
∴A点坐标为(3,4),
∴点A关于x轴的对称点的坐标是(3,﹣4),
故答案为:3;4;(3,﹣4).
15.解:∵平面直角坐标系内不同的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,
∴|2a+2|=4,
解得:a1=1,a2=﹣3.
故答案为:1或﹣3.
16.解:如图,∵△OA′B′是由△OAB绕点O按逆时针方向旋转150°得到,
∴B′落在x轴的负半轴上,OA′=OA,A′B′=AB,∠A′OB′=∠AOB=30°,
作A′M⊥OB′于M,
∴A′M=OA′==1,OM=OA′=,
∴点A′(﹣,1),
故答案为:(﹣,1).
17.解:设直线AB的解析式为y=kx+b(k≠0),将A(﹣3,2),B(3,6)分别代入得:
,
解得:,
∴y=x+4,
令x=0,得y=4,
∴AB与y轴的交点的坐标为(0,4).
故答案为:(0,4).
18.解:小军坐在教室的第3列第4行,用(3,4)表示,小红坐在第1列第6行,用(
1,6)表示,
故答案为1,6.
19.解:将点A(2,﹣3)向上平移4个单位得到点A′,
则点A′的坐标是(2,﹣3+4),即(2,1).
故答案为(2,1).
20.解:∵点(﹣3,2)与点(3,2)的横坐标互为相反数,纵坐标相同,
∴点(﹣3,2)与点(3,2)关于y轴对称,
故答案为y.
三.解答题
21.解:(1)要使点M在x轴上,a应满足2a+7=0,解得a=,
所以,当a=时,点M在x轴上;
(2)要使点M在第二象限,a应满足,解得,
所以,当时,点M在第二象限;
(3)要使点M到y轴距离是1,a应满足|a﹣1|=±1,解得a=2或a=0,
所以,当a=2或a=0时,点M到y轴距离是1.
22.解:(1)依题意得3a﹣11=2,2b﹣1=5,
∴a=,b=3.
(2)依题意得3a﹣11=﹣2,2b﹣1=﹣5,
∴a=3,b=﹣2,
∴=1.
23.解:(1)∵AB∥x轴,
∴A点和B的纵坐标相等,
即a+2=4,解得a=2,
∴A(﹣2,4),B(﹣1,4),
∴A、B两点间的距离为﹣1﹣(﹣2)=1;
(2)∵当CD⊥x轴于点D,CD=3,
∴|b|=3,解得b=3或b=﹣3,
∴当b=3时,b﹣4=﹣1;当b=﹣3时,b﹣4=﹣7,
∴C点坐标为(﹣1,3)或(﹣7,﹣3).
24.(1)根据题意,他们以中心广场为坐标原点,100m为单位长度建立直角坐标系:
(2)张明在游乐园,王励在望春亭,李华在湖心亭;
(3)中心广场(0,0),牡丹亭(300,300)
25.解:如图所示:
26.解:(1)因为点P(2﹣m,3m+6),点P在x轴的距离为9,
所以|3m+6|=9,
解得m=1或﹣5.
答:m的值为1或﹣5;
(2)因为点P在过点A(2,﹣3)且与y轴平行的直线上,
所以2﹣m=2,
解得m=0,
所以3m+6=6,
所以点P的坐标为(2,6).
27.解:(1)∵A(6,0),B(6,6),
∴△AOB是等腰直角三角形,
∴∠AOB=45°,
∵∠AOA1=120°,
∴∠A1OB=75°,
故答案为75°.
(2)作A1H⊥y轴于H.
∵OA1=6,∠A1OH=30°,
∴A1H=OA1=3,OH=A1H=3,
∴A1(﹣3,3).
(3)作B1K⊥OH于K,在B1K上取一点J,使得OJ=JB1,连接OJ.
由题意OB1=OB=6,设OK=m,则OJ=JB=2m,JK=m,
∵OK2+B1K2=B1O2,
∴m2+(2m+m)2=72,
解得m=3﹣3(负根已经舍弃),
∴KB1=3+3,
∴B1(﹣3﹣3,3﹣3).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
