沪科版八年级数学上册14.1 全等三角形课时作业(word含答案)
文档属性
| 名称 | 沪科版八年级数学上册14.1 全等三角形课时作业(word含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 135.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 20:49:56 | ||
图片预览

文档简介
沪科版数学八年级上册课时作业
第14章 全等三角形
14.1 全等三角形
基
础
达
标
1.
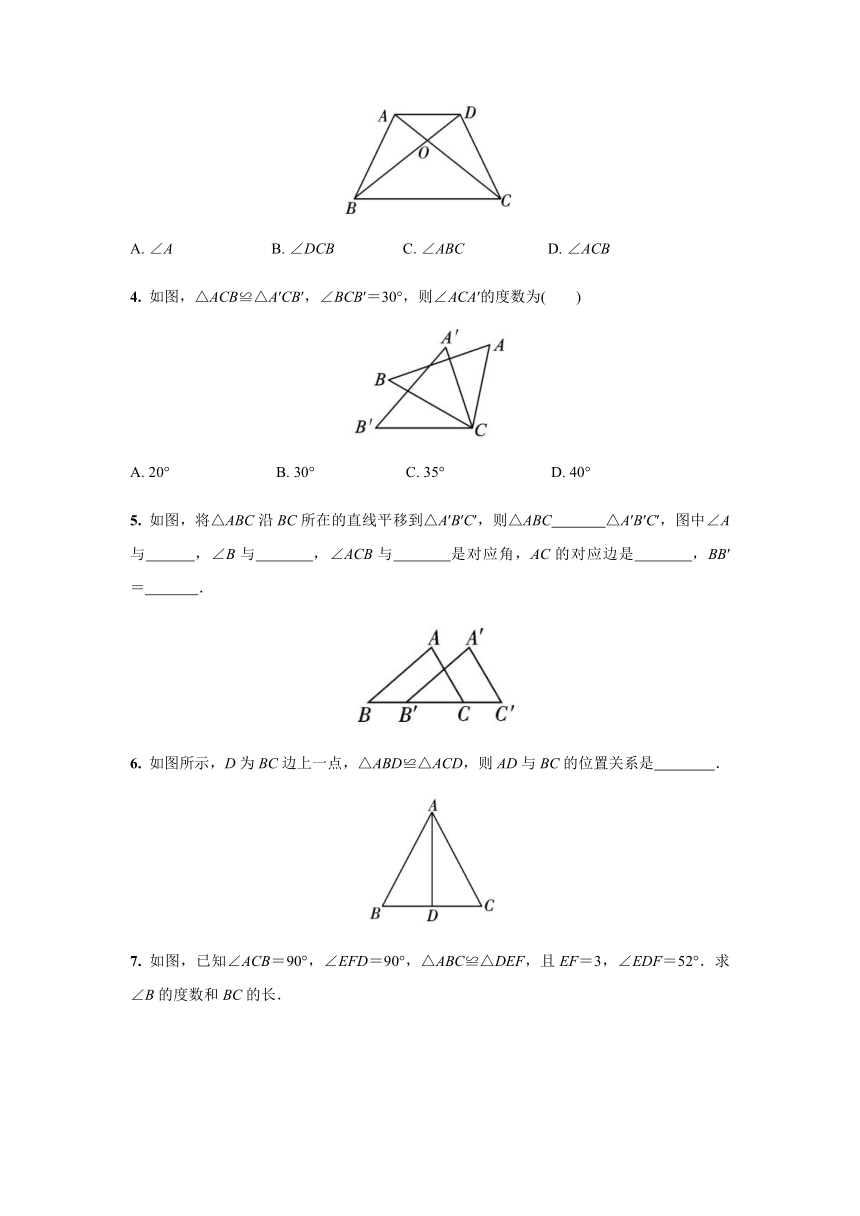
下列图形中,与左图全等的图形是(
)
A
B
C
D
2.
如图,已知△ABC≌△CDA,则与AB对应的边为(
)
A.
AD
B.
CD
C.
AC
D.
BC
3.
如图,已知△ABC≌△DCB,且AB=DC,则∠DBC等于(
)
A.
∠A
B.
∠DCB
C.
∠ABC
D.
∠ACB
4.
如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为(
)
A.
20°
B.
30°
C.
35°
D.
40°
5.
如图,将△ABC沿BC所在的直线平移到△A′B′C′,则△ABC
△A′B′C′,图中∠A与
,∠B与
,∠ACB与
是对应角,AC的对应边是
,BB′=
.
6.
如图所示,D为BC边上一点,△ABD≌△ACD,则AD与BC的位置关系是
.
7.
如图,已知∠ACB=90°,∠EFD=90°,△ABC≌△DEF,且EF=3,∠EDF=52°.求∠B的度数和BC的长.
巩
固
提
升
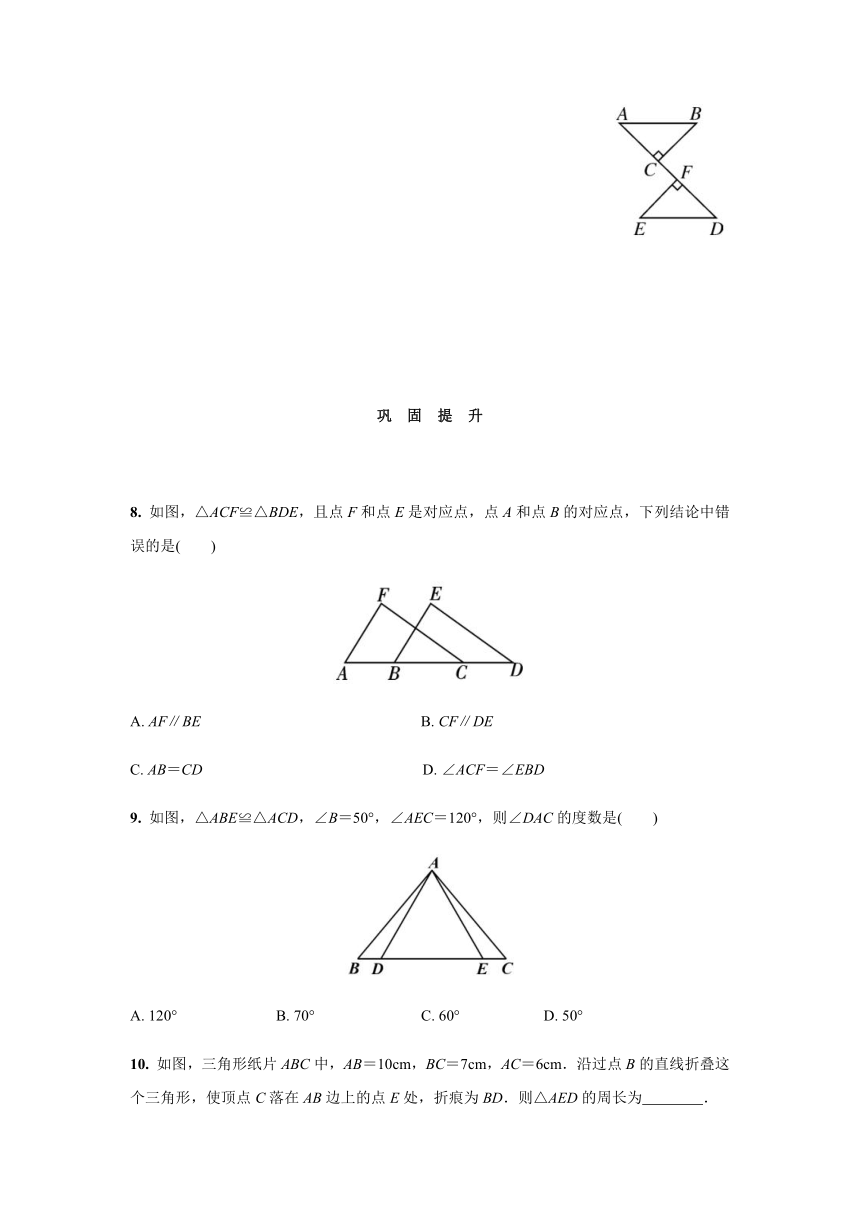
8.
如图,△ACF≌△BDE,且点F和点E是对应点,点A和点B的对应点,下列结论中错误的是(
)
A.
AF∥BE
B.
CF∥DE
C.
AB=CD
D.
∠ACF=∠EBD
9.
如图,△ABE≌△ACD,∠B=50°,∠AEC=120°,则∠DAC的度数是(
)
A.
120°
B.
70°
C.
60°
D.
50°
10.
如图,三角形纸片ABC中,AB=10cm,BC=7cm,AC=6cm.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD.则△AED的周长为
.
11.
如图,△ABD≌△CBD,若∠A=80°∠ABC=70°,则∠ADC的度数为
.
12.
如图,点A,B,C,D在一条直线上,请写出由△ABF≌△DCE可以得出的五个结论.(不再添加其它点和线段)
13.
如图,若△OAD≌△OBC,且∠O=65°,∠BEA=135°,求∠C的度数.
14.
如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并加以说明.
15.
如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)证明:BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
参
考
答
案
1.
C
2.
B
3.
D
4.
B
5.
≌
∠A′
∠A′B′C′
∠C′
A′C′
CC′
6.
垂直
7.
解:∵△ABC≌△DEF,∴BC=EF=3,∠B=∠E=90°-∠EDF=90°-52°=38°.
8.
D
9.
B
10.
9cm
11.
130°
12.
解:①AF=DE;②AB=DC;③AC=DB;④BF=CE;⑤BF∥CE.
(∠FAB=∠CDE,AF∥ED等)
13.
解:∵∠BEA为△ACE的一个外角,
∴∠BEA=∠C+∠CAE=135°,∠CAE为△OAD的一个外角,
∴∠CAE=∠O+∠D=65°+∠D,∴∠C+∠D=70°.
∵△OAD≌△OBC,∴∠C=∠D,
∴∠C=×70°=35°.
14.
解:AD∥BC,理由如下:
∵△ADF≌△CBE,∴∠ADF=∠CBE,
∴∠ADB=∠CBD,∴AD∥BC.
15.
(1)证明:∵△BAD≌△ACE,∴BD=AE,AD=CE.
∴BD=AE=AD+DE=CE+DE,即BD=DE+CE.
(2)解:△ABD满足∠ADB=90°时,BD∥CE,
理由如下:∵△BAD≌△ACE,
∴∠E=∠ADB=90°(添加的条件是∠ADB=90°).
∴∠BDE=180°-∠ADB=90°=∠E.
∴BD∥CE.
第14章 全等三角形
14.1 全等三角形
基
础
达
标
1.
下列图形中,与左图全等的图形是(
)
A
B
C
D
2.
如图,已知△ABC≌△CDA,则与AB对应的边为(
)
A.
AD
B.
CD
C.
AC
D.
BC
3.
如图,已知△ABC≌△DCB,且AB=DC,则∠DBC等于(
)
A.
∠A
B.
∠DCB
C.
∠ABC
D.
∠ACB
4.
如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为(
)
A.
20°
B.
30°
C.
35°
D.
40°
5.
如图,将△ABC沿BC所在的直线平移到△A′B′C′,则△ABC
△A′B′C′,图中∠A与
,∠B与
,∠ACB与
是对应角,AC的对应边是
,BB′=
.
6.
如图所示,D为BC边上一点,△ABD≌△ACD,则AD与BC的位置关系是
.
7.
如图,已知∠ACB=90°,∠EFD=90°,△ABC≌△DEF,且EF=3,∠EDF=52°.求∠B的度数和BC的长.
巩
固
提
升
8.
如图,△ACF≌△BDE,且点F和点E是对应点,点A和点B的对应点,下列结论中错误的是(
)
A.
AF∥BE
B.
CF∥DE
C.
AB=CD
D.
∠ACF=∠EBD
9.
如图,△ABE≌△ACD,∠B=50°,∠AEC=120°,则∠DAC的度数是(
)
A.
120°
B.
70°
C.
60°
D.
50°
10.
如图,三角形纸片ABC中,AB=10cm,BC=7cm,AC=6cm.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD.则△AED的周长为
.
11.
如图,△ABD≌△CBD,若∠A=80°∠ABC=70°,则∠ADC的度数为
.
12.
如图,点A,B,C,D在一条直线上,请写出由△ABF≌△DCE可以得出的五个结论.(不再添加其它点和线段)
13.
如图,若△OAD≌△OBC,且∠O=65°,∠BEA=135°,求∠C的度数.
14.
如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并加以说明.
15.
如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)证明:BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
参
考
答
案
1.
C
2.
B
3.
D
4.
B
5.
≌
∠A′
∠A′B′C′
∠C′
A′C′
CC′
6.
垂直
7.
解:∵△ABC≌△DEF,∴BC=EF=3,∠B=∠E=90°-∠EDF=90°-52°=38°.
8.
D
9.
B
10.
9cm
11.
130°
12.
解:①AF=DE;②AB=DC;③AC=DB;④BF=CE;⑤BF∥CE.
(∠FAB=∠CDE,AF∥ED等)
13.
解:∵∠BEA为△ACE的一个外角,
∴∠BEA=∠C+∠CAE=135°,∠CAE为△OAD的一个外角,
∴∠CAE=∠O+∠D=65°+∠D,∴∠C+∠D=70°.
∵△OAD≌△OBC,∴∠C=∠D,
∴∠C=×70°=35°.
14.
解:AD∥BC,理由如下:
∵△ADF≌△CBE,∴∠ADF=∠CBE,
∴∠ADB=∠CBD,∴AD∥BC.
15.
(1)证明:∵△BAD≌△ACE,∴BD=AE,AD=CE.
∴BD=AE=AD+DE=CE+DE,即BD=DE+CE.
(2)解:△ABD满足∠ADB=90°时,BD∥CE,
理由如下:∵△BAD≌△ACE,
∴∠E=∠ADB=90°(添加的条件是∠ADB=90°).
∴∠BDE=180°-∠ADB=90°=∠E.
∴BD∥CE.
