沪科版八年级数学上册课时作业15.2 线段的垂直平分线(word版含答案)
文档属性
| 名称 | 沪科版八年级数学上册课时作业15.2 线段的垂直平分线(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 131.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 20:51:14 | ||
图片预览

文档简介
沪科版数学八年级上册课时作业
第15章 轴对称图形与等腰三角形
15.2 线段的垂直平分线
基
础
达
标
1.
已知点P是△ABC中边AB的垂直平分线上的一点,则一定有(
)
A.
PA=PB
B.
PA=PC
C.
PB=PC
D.
点P到∠ACB的两边的距离相等
2.
在透明的纸上画线段的垂直平分线最简单方法是(
)
A.
尺规作图
B.
先量出线段中点,再用三角尺过中点画垂线
C.
折叠法
D.
以上都不对
3.
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N.作直线MN,交BC于点D,连接AD,则∠BAD的度数为(
)
A.
65°
B.
60°
C.
55°
D.
45°
4.
到三角形三个顶点距离相等的点是(
)
A.
两边垂直平分线的交点
B.
两角平分线的交点
C.
两条高的交点
D.
没有这样的点
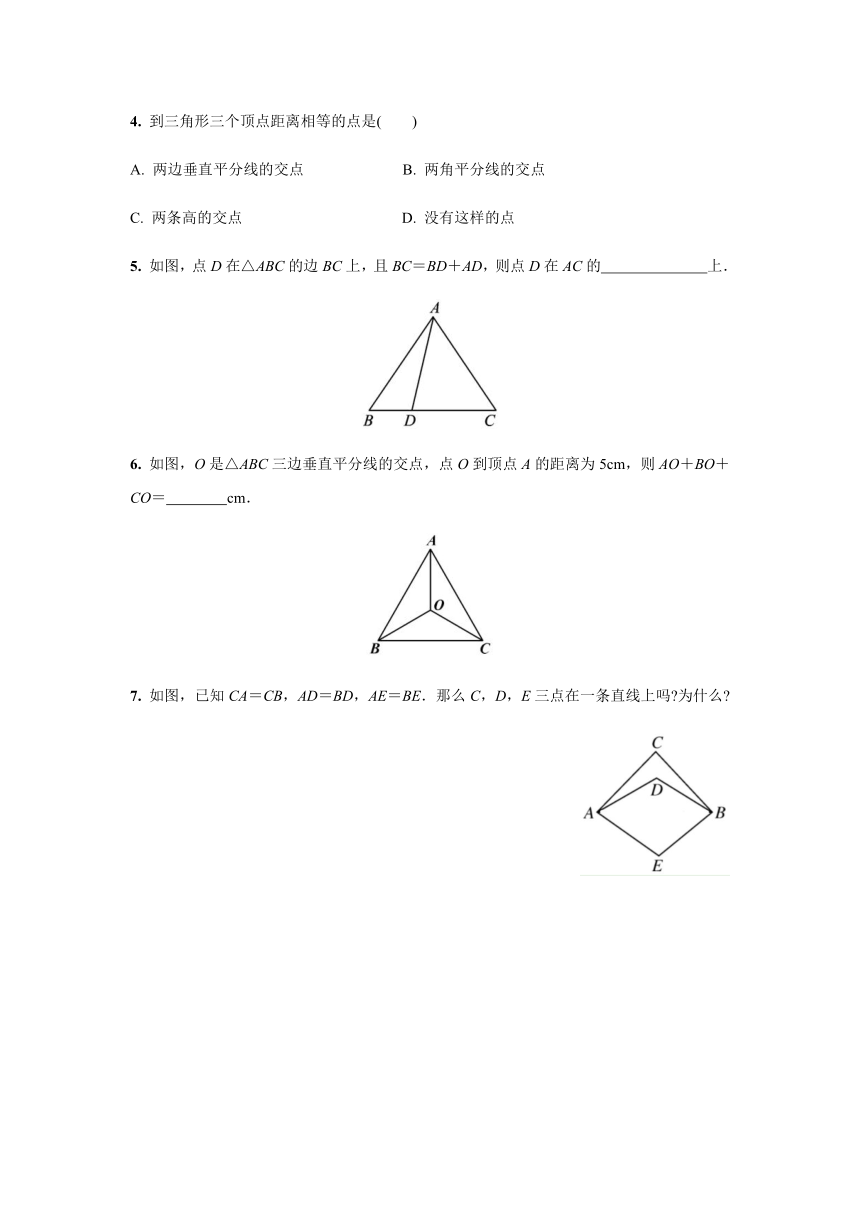
5.
如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在AC的
上.
6.
如图,O是△ABC三边垂直平分线的交点,点O到顶点A的距离为5cm,则AO+BO+CO=
cm.
7.
如图,已知CA=CB,AD=BD,AE=BE.那么C,D,E三点在一条直线上吗?为什么?
巩
固
提
升
8.
有下列说法:①若直线PE是线段AB的中垂线,则EA=EB,PA=PB;②若PA=PB,AE=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P是线段AB中垂线上的点;④若EA=EB,则经过点E的直线垂直平分线段AB.其中正确的有(
)
A.
1个
B.
2个
C.
3个
D.
4个
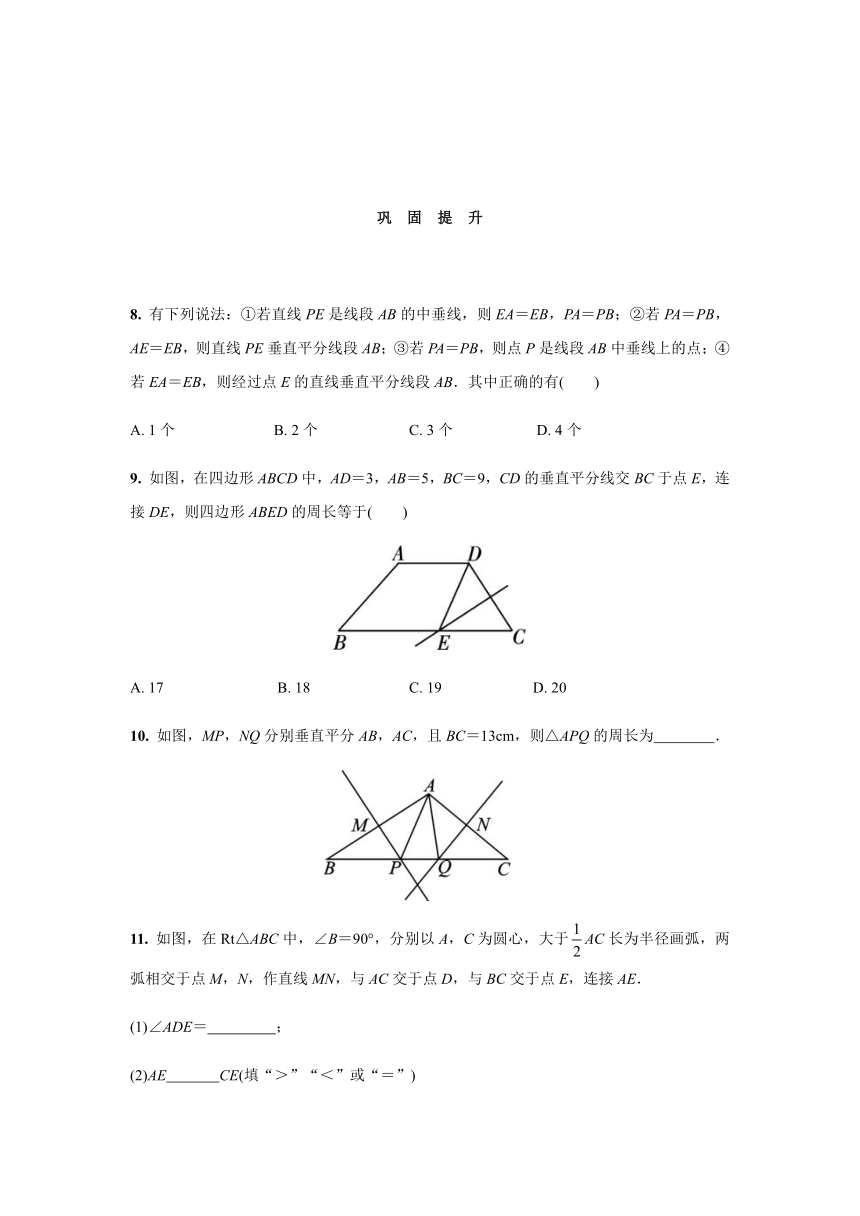
9.
如图,在四边形ABCD中,AD=3,AB=5,BC=9,CD的垂直平分线交BC于点E,连接DE,则四边形ABED的周长等于(
)
A.
17
B.
18
C.
19
D.
20
10.
如图,MP,NQ分别垂直平分AB,AC,且BC=13cm,则△APQ的周长为
.
11.
如图,在Rt△ABC中,∠B=90°,分别以A,C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
(1)∠ADE=
;
(2)AE
CE(填“>”“<”或“=”)
(3)AB=3,AC=5时,△ABE的周长是
.
12.
如图,已知AB比AC长2cm,BC的垂直平分线交AB于D,交BC于E,△ACD的周长是14cm,求AB和AC的长.
13.
如图,P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D.
求证:(1)OC=OD;
(2)OP是CD的垂直平分线.
14.
如图,平面上的四边形ABCD是一只“风筝”的骨架,其中AB=AD,CB=CD.
(1)小明同学观察了这个“风筝”的骨架后,他认为四边形ABCD的两条对角线AC⊥BD,垂足为E,并且BE=ED,你同意小明的判断吗?请充分说明理由.
(2)设对角线AC=a,BD=b,请用含a,b的代数式表示四边形ABCD的面积.
参
考
答
案
1.
A
2.
C
3.
A
4.
A
5.
垂直平分线
6.
15
7.
解:C,D,E三点在同一条直线上.连接AB,∵CA=CB,AD=BD,∴C,D两点在线段AB的垂直平分线上.∵AD=BD,AE=BE,∴D、E两点在线段AB的垂直平分线上.∴C,D,E三点都在AB的垂直平分线上.
8.
C
9.
A
10.
13cm
11.
(1)90°
(2)=
(3)7
12.
解:∵DE垂直平分BC,∴BD=CD,∵△ACD的周长是14cm,即AD+CD+AC=14cm,∴AD+BD+AC=14cm,即AB+AC=14cm,又AB-AC=2cm,联立得
解得
∴AB=8cm,AC=6cm.
13.
证明:(1)∵OP平分∠AOB.∴∠AOP=∠BOP.∵PC⊥OA,PD⊥OB,∴∠PCO=∠PDO=90°,在△COP与△DOP中,
∴△COP≌△DOP.(AAS)
∴OC=OD,PC=PD.
(2)∵OC=OD,PC=PD,∴点O,P在CD的垂直平分线上.∴OP是CD的垂直平分线.
14.
解:(1)同意.∵BA=AD,BC=DC.∴A,C在BD的垂直平分线上,即AC垂直平分BD,∴BE=ED,AC⊥BD.
(2)S四边形ABCD=BD﹒AE+BD﹒EC=BD﹒(AE+EC)=BD﹒AC=ab.
第15章 轴对称图形与等腰三角形
15.2 线段的垂直平分线
基
础
达
标
1.
已知点P是△ABC中边AB的垂直平分线上的一点,则一定有(
)
A.
PA=PB
B.
PA=PC
C.
PB=PC
D.
点P到∠ACB的两边的距离相等
2.
在透明的纸上画线段的垂直平分线最简单方法是(
)
A.
尺规作图
B.
先量出线段中点,再用三角尺过中点画垂线
C.
折叠法
D.
以上都不对
3.
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N.作直线MN,交BC于点D,连接AD,则∠BAD的度数为(
)
A.
65°
B.
60°
C.
55°
D.
45°
4.
到三角形三个顶点距离相等的点是(
)
A.
两边垂直平分线的交点
B.
两角平分线的交点
C.
两条高的交点
D.
没有这样的点
5.
如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在AC的
上.
6.
如图,O是△ABC三边垂直平分线的交点,点O到顶点A的距离为5cm,则AO+BO+CO=
cm.
7.
如图,已知CA=CB,AD=BD,AE=BE.那么C,D,E三点在一条直线上吗?为什么?
巩
固
提
升
8.
有下列说法:①若直线PE是线段AB的中垂线,则EA=EB,PA=PB;②若PA=PB,AE=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P是线段AB中垂线上的点;④若EA=EB,则经过点E的直线垂直平分线段AB.其中正确的有(
)
A.
1个
B.
2个
C.
3个
D.
4个
9.
如图,在四边形ABCD中,AD=3,AB=5,BC=9,CD的垂直平分线交BC于点E,连接DE,则四边形ABED的周长等于(
)
A.
17
B.
18
C.
19
D.
20
10.
如图,MP,NQ分别垂直平分AB,AC,且BC=13cm,则△APQ的周长为
.
11.
如图,在Rt△ABC中,∠B=90°,分别以A,C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
(1)∠ADE=
;
(2)AE
CE(填“>”“<”或“=”)
(3)AB=3,AC=5时,△ABE的周长是
.
12.
如图,已知AB比AC长2cm,BC的垂直平分线交AB于D,交BC于E,△ACD的周长是14cm,求AB和AC的长.
13.
如图,P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D.
求证:(1)OC=OD;
(2)OP是CD的垂直平分线.
14.
如图,平面上的四边形ABCD是一只“风筝”的骨架,其中AB=AD,CB=CD.
(1)小明同学观察了这个“风筝”的骨架后,他认为四边形ABCD的两条对角线AC⊥BD,垂足为E,并且BE=ED,你同意小明的判断吗?请充分说明理由.
(2)设对角线AC=a,BD=b,请用含a,b的代数式表示四边形ABCD的面积.
参
考
答
案
1.
A
2.
C
3.
A
4.
A
5.
垂直平分线
6.
15
7.
解:C,D,E三点在同一条直线上.连接AB,∵CA=CB,AD=BD,∴C,D两点在线段AB的垂直平分线上.∵AD=BD,AE=BE,∴D、E两点在线段AB的垂直平分线上.∴C,D,E三点都在AB的垂直平分线上.
8.
C
9.
A
10.
13cm
11.
(1)90°
(2)=
(3)7
12.
解:∵DE垂直平分BC,∴BD=CD,∵△ACD的周长是14cm,即AD+CD+AC=14cm,∴AD+BD+AC=14cm,即AB+AC=14cm,又AB-AC=2cm,联立得
解得
∴AB=8cm,AC=6cm.
13.
证明:(1)∵OP平分∠AOB.∴∠AOP=∠BOP.∵PC⊥OA,PD⊥OB,∴∠PCO=∠PDO=90°,在△COP与△DOP中,
∴△COP≌△DOP.(AAS)
∴OC=OD,PC=PD.
(2)∵OC=OD,PC=PD,∴点O,P在CD的垂直平分线上.∴OP是CD的垂直平分线.
14.
解:(1)同意.∵BA=AD,BC=DC.∴A,C在BD的垂直平分线上,即AC垂直平分BD,∴BE=ED,AC⊥BD.
(2)S四边形ABCD=BD﹒AE+BD﹒EC=BD﹒(AE+EC)=BD﹒AC=ab.
