人教八上数学12.2.4直角三角形全等的判定.课件(45张ppt)
文档属性
| 名称 | 人教八上数学12.2.4直角三角形全等的判定.课件(45张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 21:22:10 | ||
图片预览


文档简介
(共45张PPT)
学习目标
1.探索并掌握两个直角三角形全等的条件:HL,并能应用它判别两个直角三角形是否全等.
教学重点:理解,掌握三角形全等的条件HL
2.经历作图、比较、证明等探究过程,提高分析、作图、归纳、表达、逻辑推理等能力;并通过对知识方法的总结,培养反思的习惯,培养理性思维.
3.提高应用数学的意识.
教学难点:应用HL解决有关问题
复
习:
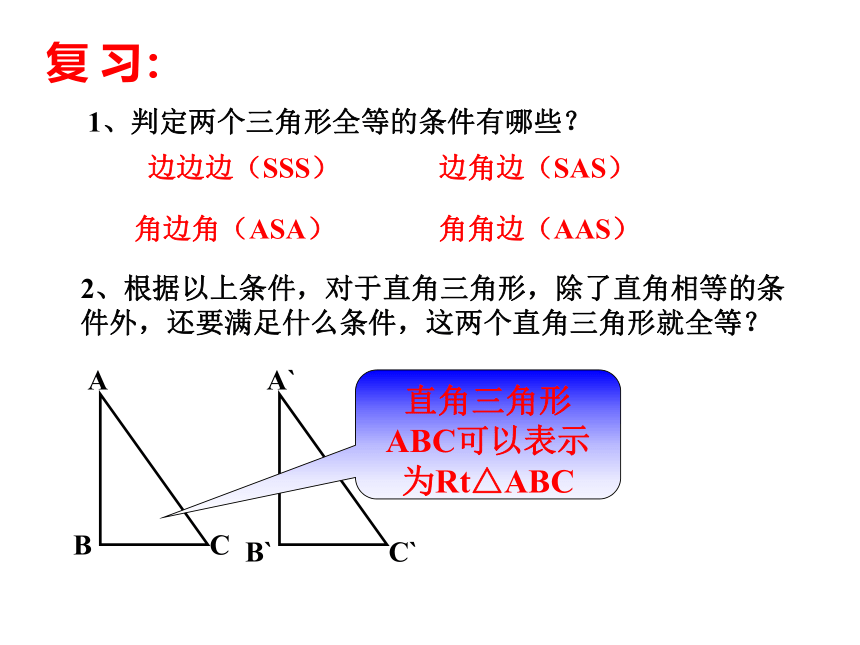
1、判定两个三角形全等的条件有哪些?
边角边(SAS)
2、根据以上条件,对于直角三角形,除了直角相等的条件外,还要满足什么条件,这两个直角三角形就全等?
A
B
C
A`
B`
C`
直角三角形ABC可以表示为Rt△ABC
边边边(SSS)
角角边(AAS)
角边角(ASA)
讨
论:
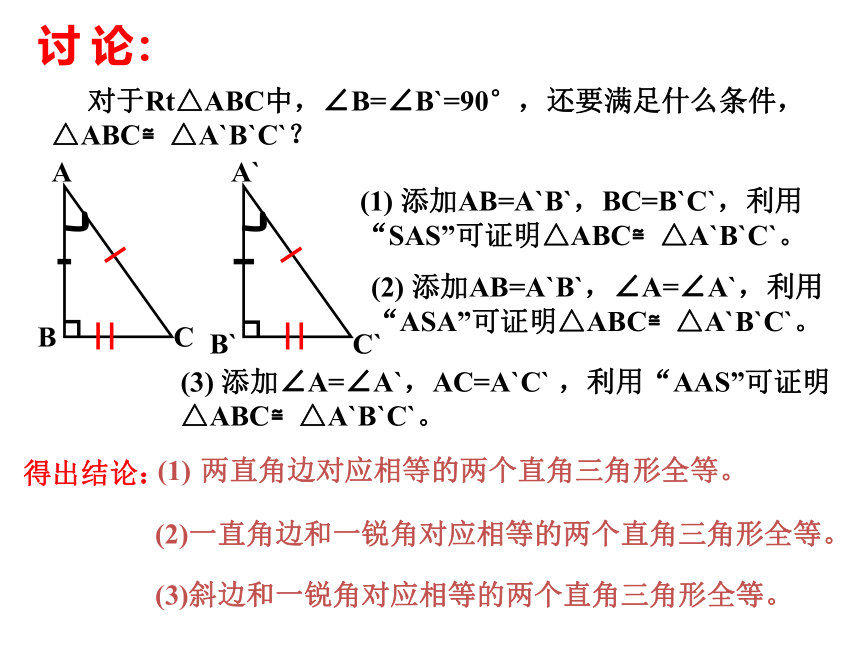
对于Rt△ABC中,∠B=∠B`=90°,还要满足什么条件,△ABC≌△A`B`C`?
A
B
C
A`
B`
C`
(1)
添加AB=A`B`,BC=B`C`,利用“SAS”可证明△ABC≌△A`B`C`。
(2)
添加AB=A`B`,∠A=∠A`,利用“ASA”可证明△ABC≌△A`B`C`。
(3)
添加∠A=∠A`,AC=A`C`
,利用“AAS”可证明△ABC≌△A`B`C`。
得出结论:
两直角边对应相等的两个直角三角形全等。
(2)一直角边和一锐角对应相等的两个直角三角形全等。
(3)斜边和一锐角对应相等的两个直角三角形全等。
┓
┓
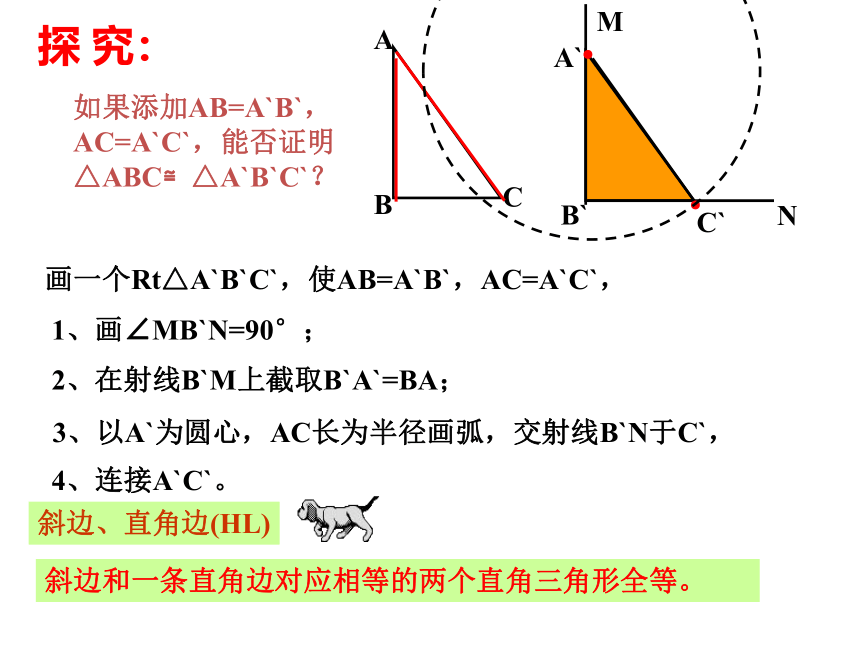
如果添加AB=A`B`,AC=A`C`,能否证明
△ABC≌△A`B`C`?
A
B
C
A`
B`
C`
探
究:
M
N
●
●
画一个Rt△A`B`C`,使AB=A`B`,AC=A`C`,
1、画∠MB`N=90°;
2、在射线B`M上截取B`A`=BA;
3、以A`为圆心,AC长为半径画弧,交射线B`N于C`,
4、连接A`C`。
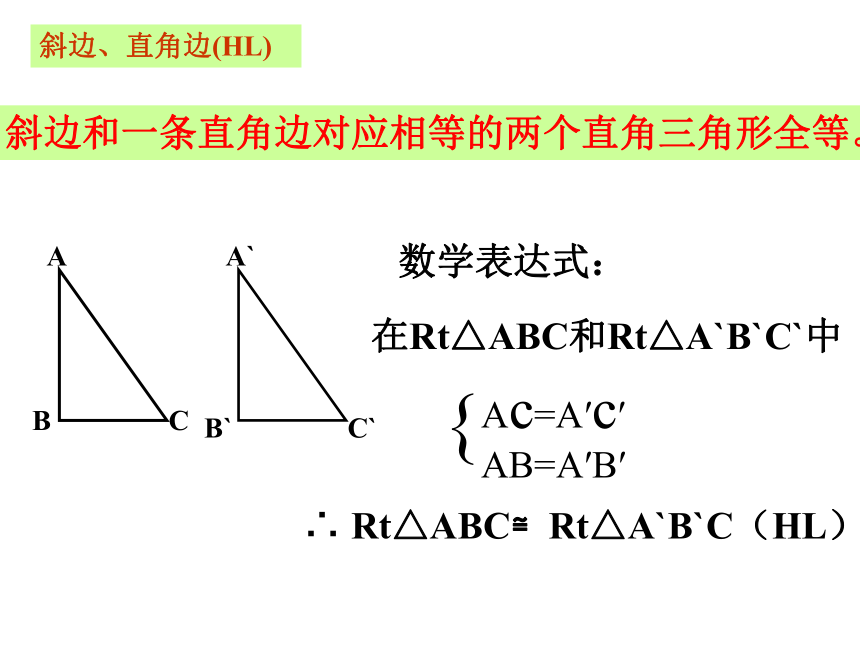
斜边、直角边(HL)
斜边和一条直角边对应相等的两个直角三角形全等。
判定公理:
有斜边和一条直角边对应相等的
两个直角三角形全等.
条件1
条件2
前提
斜边和一条直角边对应相等的两个直角三角形全等。
斜边、直角边(HL)
A
B
C
A`
B`
C`
在Rt△ABC和Rt△A`B`C`中
∴
Rt△ABC≌Rt△A`B`C(HL)
数学表达式:
{
Ac=A′c′
AB=A′B′
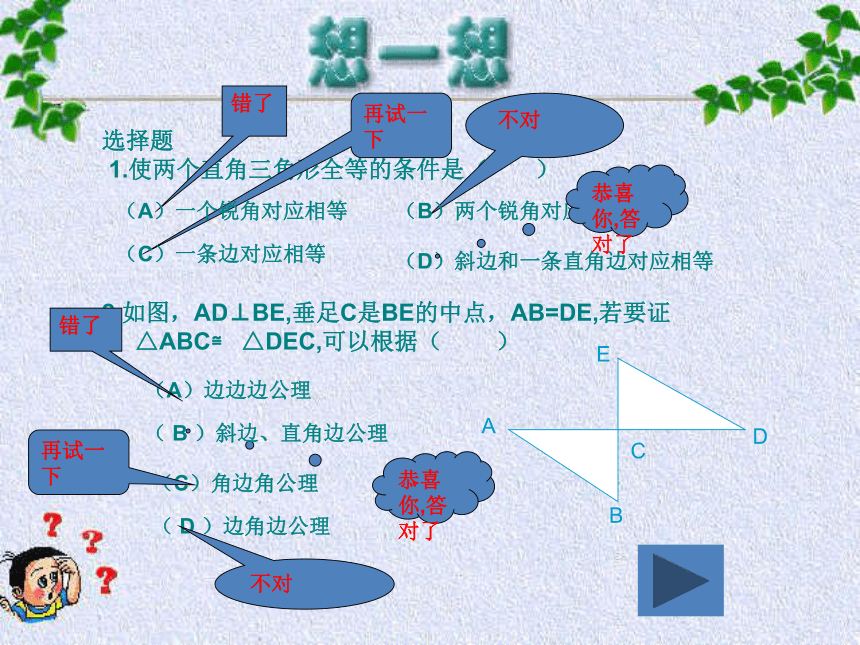
选择题
1.使两个直角三角形全等的条件是(
)
2.如图,AD⊥BE,垂足C是BE的中点,AB=DE,若要证
△ABC≌
△DEC,可以根据(
)
A
E
D
B
C
错了
不对
恭喜你,答对了
再试一下
(A)一个锐角对应相等
(B)两个锐角对应相等
(C)一条边对应相等
(D)斜边和一条直角边对应相等
(A)边边边公理
(
D
)边角边公理
(C)角边角公理
(
B
)斜边、直角边公理
错了
再试一下
不对
恭喜你,答对了
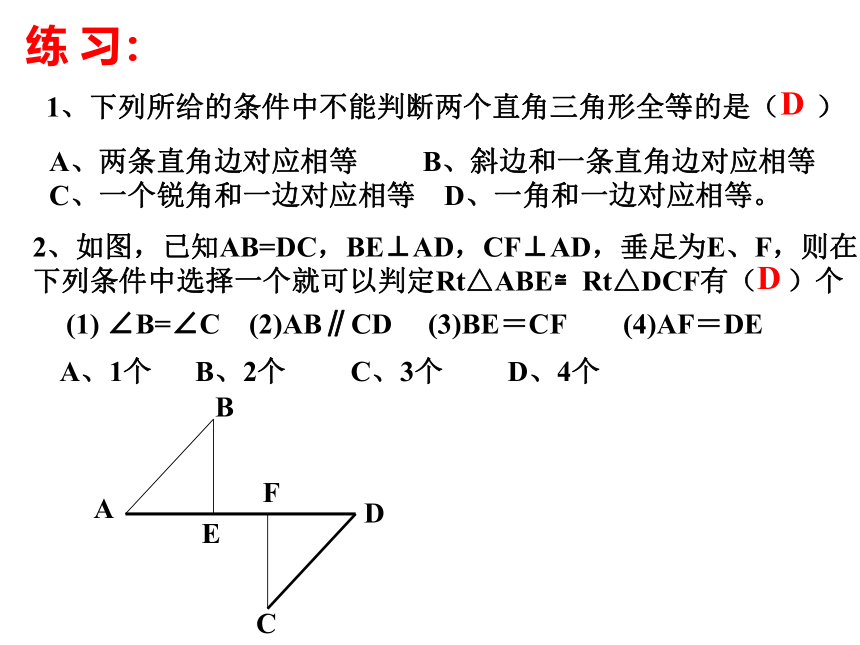
练
习:
1、下列所给的条件中不能判断两个直角三角形全等的是(
)
A、两条直角边对应相等
B、斜边和一条直角边对应相等
C、一个锐角和一边对应相等
D、一角和一边对应相等。
2、如图,已知AB=DC,BE⊥AD,CF⊥AD,垂足为E、F,则在下列条件中选择一个就可以判定Rt△ABE≌Rt△DCF有(
)个
(1)
∠B=∠C
(2)AB∥CD
(3)BE=CF
(4)AF=DE
A、1个
B、2个
C、3个
D、4个
A
B
E
F
C
D
D
D
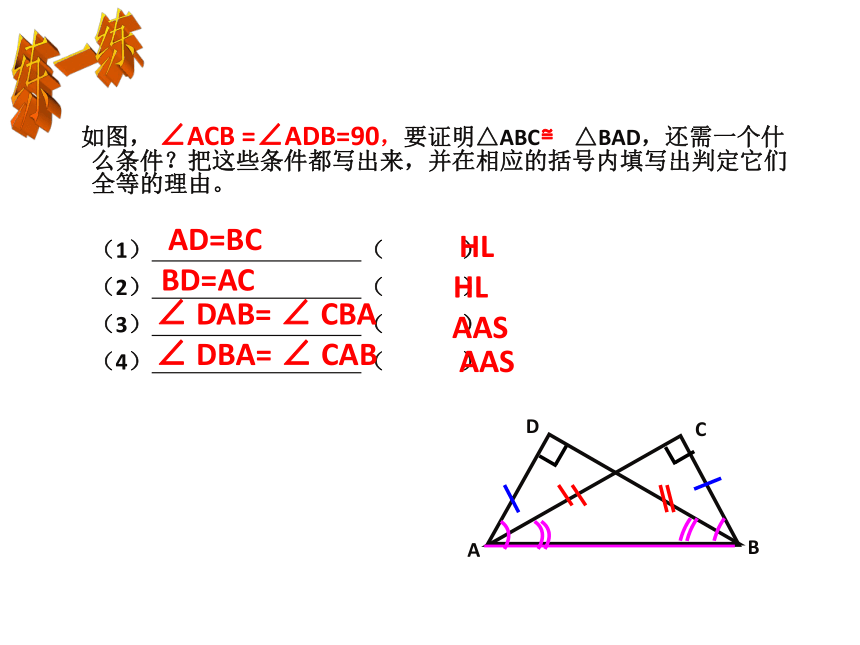
如图,
∠ACB
=∠ADB=90,要证明△ABC≌
△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由。
(1)
(
)
(2)
(
)
(3)
(
)
(4)
(
)
A
B
D
C
AD=BC
∠
DAB=
∠
CBA
BD=AC
∠
DBA=
∠
CAB
HL
HL
AAS
AAS
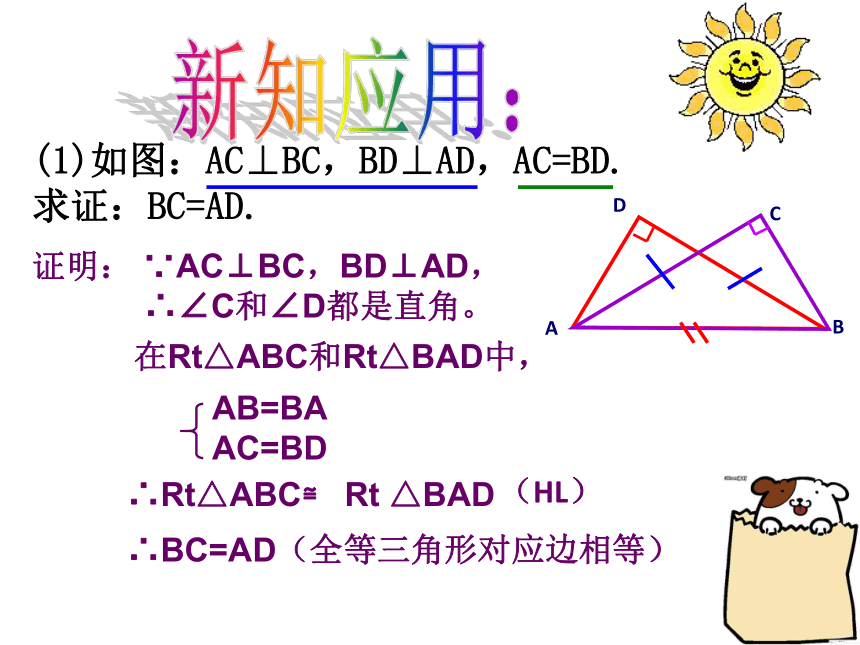
(1)如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.
A
B
C
D
证明:
∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角。
在Rt△ABC和Rt△BAD中,
AB=BA
AC=BD
∴Rt△ABC≌
Rt
△BAD
∴BC=AD
(HL)
(全等三角形对应边相等)
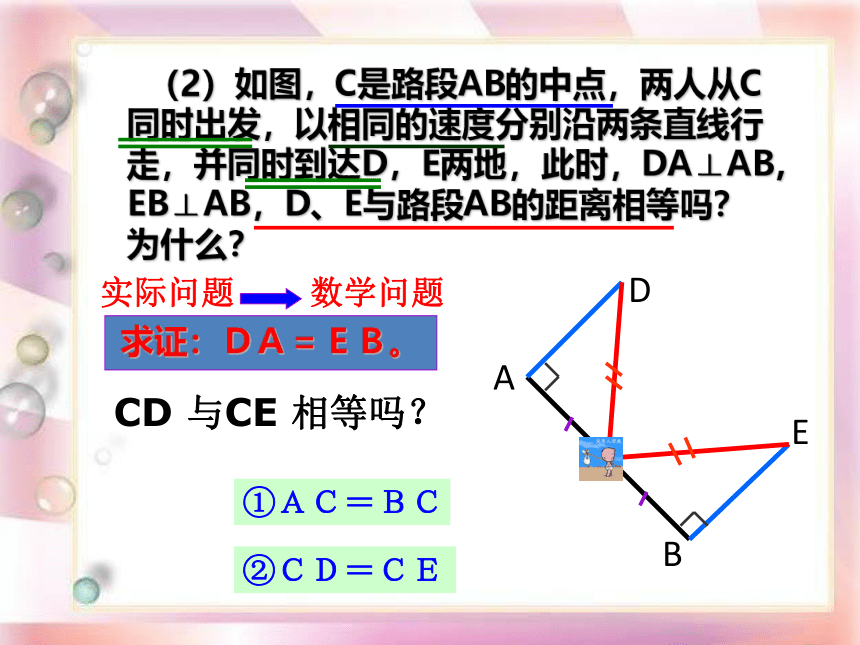
(2)如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?
B
D
A
C
E
实际问题
数学问题
求证:DA=EB。
①AC=BC
②CD=CE
CD
与CE
相等吗?
证明:
∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。
AC=BC
DC=EC
∴Rt△ACD≌
Rt
△BCE(HL)
∴
DA=EB
在Rt△ACD和Rt△BCE中,
又∵C是AB的中点,
∴AC=BC
∵C到D、E的速度、时间相同,
∴DC=EC
B
D
A
C
E
(全等三角形对应边相等)
(3)如图,AB=CD,AE
⊥BC,DF
⊥BC,
CE=BF.
求证:AE=DF.
A
B
C
D
E
F
课本14页练习
∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
(3)如图,AB=CD,AE
⊥BC,DF
⊥BC,
CE=BF.
求证:AE=DF.
A
B
C
D
E
F
课本103页练习
证明:∵
AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。
又∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
在Rt△ABE和Rt△DCF中
CE=BF
AB=DC
∴Rt△ABE≌Rt△DCF(HL)
∴AE=DF
判断两个直角三角形全等的方法有:
(1):
;
(2):
;
(3):
;
(4):
;
SSS
SAS
ASA
AAS
(5):
;
HL
1、
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
问题
&
探索
?
A
B
C
D
E
F
1、
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
问题
&
探索
?
A
B
C
D
E
F
解:∠ABC+∠DFE=90°.理由如下:
在Rt△ABC和Rt△DEF中,
则
BC=EF,
AC=DF
.
∴
Rt△ABC≌Rt△DEF
(HL).
∴∠ABC=∠DEF
(全等三角形对应角相等).
又
∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
延伸
&
拓展
?
如图,E,F分别为线段AC上的两个点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.
求证:MB=MD,ME=MF;
A
B
C
D
E
F
M
如图,E,F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.
当E、F两点移动至如图的位置时,其余条件不变,上述结论能否成立?若成立,请给予证明.
延伸
拓展
D
A
B
C
E
F
M
已知:如图,AC⊥CB,DB⊥CB,AB=DC,求证:∠ACD=∠DBA
A
B
D
C
如图,AD、A`D`分别是△ABC和△A`B`C`中BC、B`C`边上的高,且AB=A`B`,AD=A`D`,若使△ABC≌△A`B`C`,请补充条件(只需填写一个你认为适当的条件)______________________。
A
B
C
D
A`
B`
C`
D`
这节课你有那些收获?
已知:如图,在△ABC和△BAD中,AC⊥BC,
AD⊥BD,垂足分别为C,D,
BC=AD,
求证:AC=BD.
A
B
D
C
旧知回顾
判断两个三角形全等的方法
我们已经学了哪些呢?
SSS
SAS
ASA
AAS
三边对应相等的两个三角形全等。(简写成
“边边边”或“SSS”)
D
E
F
A
B
C
“边角边”或“SAS”)
两边和它们夹角对应相等的两个三角形全等。(简写成
D
E
F
A
B
C
“有两边及其中一边的对角对应相等”的两个三角形不一定全等。
A
B
C
D
“角边角”或“ASA”)
两角和它们的夹边对应相等的两个三角形全等。(简写成
D
E
F
A
B
C
D
E
F
A
B
C
两个角和其中一个角的对边对应相等的两个三角形全等.(简写成
“角角边”或“AAS”)
如图,△ABC中,∠
C
=90°,直角边是_____、_____,斜边是______。
C
B
A
我们把直角△ABC记作Rt△ABC。
AC
BC
AB
以上的四种判别三角形全等的
方法能不能用来判别Rt△全等呢?
思考:
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。
情境问题1:
情境问题1:
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。
你能帮工作人员想个办法吗?
A
B
D
F
C
E
情境问题1:
∠B=∠F=Rt
∠
则利用
可判定全等;
①若测得AB=DF,∠A=∠D,
则利用
可判定全等;
A
SA
②若测得AB=DF,∠C=∠E,
A
AS
③若测得AC=DE,∠C=∠E,
则利用
可判定全等;
A
AS
④若测得AC=DE,∠A=∠D,
则利用
可判定全等;
A
AS
⑤若测得AC=DE,∠A=∠D,AB=DE,
则利用
可判定全等;
S
AS
A
B
D
F
C
E
情境问题2:
如果工作人员只带了一条皮尺,能完成这项任务吗?
A
B
D
F
C
E
工作人员是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”。你相信他的结论吗?
情境问题2:
对于两个直角三角形,若满足一条直角边和一条斜边对应相等时,这两个直角三角形全等吗?
A
B
D
F
C
E
任意画出一个Rt△ABC,∠C=90°。
∟
B
C
A
B?
A?
按照下面的步骤画Rt△A?B?C?
⑴
作∠MC?N=90°;
⑵
在射线C?M上取段B?C?=BC;
⑶
以B?为圆心,AB为半径画弧,交
射线C?N于点A?;
⑷
连接A?B?.
∟
C?
M
N
请你动手画一画
再画一个Rt△A?B?C?,使得∠C?=
90°,
B?C?=BC,A?B?=
AB。
把你所画的三角形撕出来,与原三角形进行比较,看是否能重合?
亲
自
实
践
任意画出一个Rt△ABC,∠C=90°。再画一个Rt△A?B?C?,使得∠C?=
90°,
B?C?=BC,A?B?=
AB。
B?
A?
按照下面的步骤画一画
⑴
作∠MC?N=90°;
⑵
在射线C?M上取段B?C?=BC;
⑶
以B?为圆心,AB为半径画弧,交
射线C?N于点A?;
⑷
连接A?B?.
∟
C?
M
N
请你动手画一画
∟
B
?
C
?
A
?
∟
B
C
A
现象:
两个直角三角形能重合。
说明:
当一个直角三角形的一条直角边和
斜边确定后,
那么它的形状和大小
也被确定.
判定公理:
有斜边和一条直角边对应相等的
两个直角三角形全等.
条件1
条件2
前提
斜边和一条直角边对应相等的两个直角三角形全等.
简写:“斜边、直角边”或“HL”
A
B=A?B?
A
C=
A?C?(
或BC=
B?C?)
∴Rt△ABC≌Rt△
A?B?C?(H
L)
直角三角形全等的判定方法:
证明:在Rt△ABC与Rt△
A?B?C?中
通过刚才的探索,发现工作人员的做法
是完全正确的。
学习目标
1.探索并掌握两个直角三角形全等的条件:HL,并能应用它判别两个直角三角形是否全等.
教学重点:理解,掌握三角形全等的条件HL
2.经历作图、比较、证明等探究过程,提高分析、作图、归纳、表达、逻辑推理等能力;并通过对知识方法的总结,培养反思的习惯,培养理性思维.
3.提高应用数学的意识.
教学难点:应用HL解决有关问题
复
习:
1、判定两个三角形全等的条件有哪些?
边角边(SAS)
2、根据以上条件,对于直角三角形,除了直角相等的条件外,还要满足什么条件,这两个直角三角形就全等?
A
B
C
A`
B`
C`
直角三角形ABC可以表示为Rt△ABC
边边边(SSS)
角角边(AAS)
角边角(ASA)
讨
论:
对于Rt△ABC中,∠B=∠B`=90°,还要满足什么条件,△ABC≌△A`B`C`?
A
B
C
A`
B`
C`
(1)
添加AB=A`B`,BC=B`C`,利用“SAS”可证明△ABC≌△A`B`C`。
(2)
添加AB=A`B`,∠A=∠A`,利用“ASA”可证明△ABC≌△A`B`C`。
(3)
添加∠A=∠A`,AC=A`C`
,利用“AAS”可证明△ABC≌△A`B`C`。
得出结论:
两直角边对应相等的两个直角三角形全等。
(2)一直角边和一锐角对应相等的两个直角三角形全等。
(3)斜边和一锐角对应相等的两个直角三角形全等。
┓
┓
如果添加AB=A`B`,AC=A`C`,能否证明
△ABC≌△A`B`C`?
A
B
C
A`
B`
C`
探
究:
M
N
●
●
画一个Rt△A`B`C`,使AB=A`B`,AC=A`C`,
1、画∠MB`N=90°;
2、在射线B`M上截取B`A`=BA;
3、以A`为圆心,AC长为半径画弧,交射线B`N于C`,
4、连接A`C`。
斜边、直角边(HL)
斜边和一条直角边对应相等的两个直角三角形全等。
判定公理:
有斜边和一条直角边对应相等的
两个直角三角形全等.
条件1
条件2
前提
斜边和一条直角边对应相等的两个直角三角形全等。
斜边、直角边(HL)
A
B
C
A`
B`
C`
在Rt△ABC和Rt△A`B`C`中
∴
Rt△ABC≌Rt△A`B`C(HL)
数学表达式:
{
Ac=A′c′
AB=A′B′
选择题
1.使两个直角三角形全等的条件是(
)
2.如图,AD⊥BE,垂足C是BE的中点,AB=DE,若要证
△ABC≌
△DEC,可以根据(
)
A
E
D
B
C
错了
不对
恭喜你,答对了
再试一下
(A)一个锐角对应相等
(B)两个锐角对应相等
(C)一条边对应相等
(D)斜边和一条直角边对应相等
(A)边边边公理
(
D
)边角边公理
(C)角边角公理
(
B
)斜边、直角边公理
错了
再试一下
不对
恭喜你,答对了
练
习:
1、下列所给的条件中不能判断两个直角三角形全等的是(
)
A、两条直角边对应相等
B、斜边和一条直角边对应相等
C、一个锐角和一边对应相等
D、一角和一边对应相等。
2、如图,已知AB=DC,BE⊥AD,CF⊥AD,垂足为E、F,则在下列条件中选择一个就可以判定Rt△ABE≌Rt△DCF有(
)个
(1)
∠B=∠C
(2)AB∥CD
(3)BE=CF
(4)AF=DE
A、1个
B、2个
C、3个
D、4个
A
B
E
F
C
D
D
D
如图,
∠ACB
=∠ADB=90,要证明△ABC≌
△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由。
(1)
(
)
(2)
(
)
(3)
(
)
(4)
(
)
A
B
D
C
AD=BC
∠
DAB=
∠
CBA
BD=AC
∠
DBA=
∠
CAB
HL
HL
AAS
AAS
(1)如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.
A
B
C
D
证明:
∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角。
在Rt△ABC和Rt△BAD中,
AB=BA
AC=BD
∴Rt△ABC≌
Rt
△BAD
∴BC=AD
(HL)
(全等三角形对应边相等)
(2)如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?
B
D
A
C
E
实际问题
数学问题
求证:DA=EB。
①AC=BC
②CD=CE
CD
与CE
相等吗?
证明:
∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。
AC=BC
DC=EC
∴Rt△ACD≌
Rt
△BCE(HL)
∴
DA=EB
在Rt△ACD和Rt△BCE中,
又∵C是AB的中点,
∴AC=BC
∵C到D、E的速度、时间相同,
∴DC=EC
B
D
A
C
E
(全等三角形对应边相等)
(3)如图,AB=CD,AE
⊥BC,DF
⊥BC,
CE=BF.
求证:AE=DF.
A
B
C
D
E
F
课本14页练习
∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
(3)如图,AB=CD,AE
⊥BC,DF
⊥BC,
CE=BF.
求证:AE=DF.
A
B
C
D
E
F
课本103页练习
证明:∵
AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。
又∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
在Rt△ABE和Rt△DCF中
CE=BF
AB=DC
∴Rt△ABE≌Rt△DCF(HL)
∴AE=DF
判断两个直角三角形全等的方法有:
(1):
;
(2):
;
(3):
;
(4):
;
SSS
SAS
ASA
AAS
(5):
;
HL
1、
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
问题
&
探索
?
A
B
C
D
E
F
1、
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
问题
&
探索
?
A
B
C
D
E
F
解:∠ABC+∠DFE=90°.理由如下:
在Rt△ABC和Rt△DEF中,
则
BC=EF,
AC=DF
.
∴
Rt△ABC≌Rt△DEF
(HL).
∴∠ABC=∠DEF
(全等三角形对应角相等).
又
∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
延伸
&
拓展
?
如图,E,F分别为线段AC上的两个点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.
求证:MB=MD,ME=MF;
A
B
C
D
E
F
M
如图,E,F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.
当E、F两点移动至如图的位置时,其余条件不变,上述结论能否成立?若成立,请给予证明.
延伸
拓展
D
A
B
C
E
F
M
已知:如图,AC⊥CB,DB⊥CB,AB=DC,求证:∠ACD=∠DBA
A
B
D
C
如图,AD、A`D`分别是△ABC和△A`B`C`中BC、B`C`边上的高,且AB=A`B`,AD=A`D`,若使△ABC≌△A`B`C`,请补充条件(只需填写一个你认为适当的条件)______________________。
A
B
C
D
A`
B`
C`
D`
这节课你有那些收获?
已知:如图,在△ABC和△BAD中,AC⊥BC,
AD⊥BD,垂足分别为C,D,
BC=AD,
求证:AC=BD.
A
B
D
C
旧知回顾
判断两个三角形全等的方法
我们已经学了哪些呢?
SSS
SAS
ASA
AAS
三边对应相等的两个三角形全等。(简写成
“边边边”或“SSS”)
D
E
F
A
B
C
“边角边”或“SAS”)
两边和它们夹角对应相等的两个三角形全等。(简写成
D
E
F
A
B
C
“有两边及其中一边的对角对应相等”的两个三角形不一定全等。
A
B
C
D
“角边角”或“ASA”)
两角和它们的夹边对应相等的两个三角形全等。(简写成
D
E
F
A
B
C
D
E
F
A
B
C
两个角和其中一个角的对边对应相等的两个三角形全等.(简写成
“角角边”或“AAS”)
如图,△ABC中,∠
C
=90°,直角边是_____、_____,斜边是______。
C
B
A
我们把直角△ABC记作Rt△ABC。
AC
BC
AB
以上的四种判别三角形全等的
方法能不能用来判别Rt△全等呢?
思考:
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。
情境问题1:
情境问题1:
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。
你能帮工作人员想个办法吗?
A
B
D
F
C
E
情境问题1:
∠B=∠F=Rt
∠
则利用
可判定全等;
①若测得AB=DF,∠A=∠D,
则利用
可判定全等;
A
SA
②若测得AB=DF,∠C=∠E,
A
AS
③若测得AC=DE,∠C=∠E,
则利用
可判定全等;
A
AS
④若测得AC=DE,∠A=∠D,
则利用
可判定全等;
A
AS
⑤若测得AC=DE,∠A=∠D,AB=DE,
则利用
可判定全等;
S
AS
A
B
D
F
C
E
情境问题2:
如果工作人员只带了一条皮尺,能完成这项任务吗?
A
B
D
F
C
E
工作人员是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”。你相信他的结论吗?
情境问题2:
对于两个直角三角形,若满足一条直角边和一条斜边对应相等时,这两个直角三角形全等吗?
A
B
D
F
C
E
任意画出一个Rt△ABC,∠C=90°。
∟
B
C
A
B?
A?
按照下面的步骤画Rt△A?B?C?
⑴
作∠MC?N=90°;
⑵
在射线C?M上取段B?C?=BC;
⑶
以B?为圆心,AB为半径画弧,交
射线C?N于点A?;
⑷
连接A?B?.
∟
C?
M
N
请你动手画一画
再画一个Rt△A?B?C?,使得∠C?=
90°,
B?C?=BC,A?B?=
AB。
把你所画的三角形撕出来,与原三角形进行比较,看是否能重合?
亲
自
实
践
任意画出一个Rt△ABC,∠C=90°。再画一个Rt△A?B?C?,使得∠C?=
90°,
B?C?=BC,A?B?=
AB。
B?
A?
按照下面的步骤画一画
⑴
作∠MC?N=90°;
⑵
在射线C?M上取段B?C?=BC;
⑶
以B?为圆心,AB为半径画弧,交
射线C?N于点A?;
⑷
连接A?B?.
∟
C?
M
N
请你动手画一画
∟
B
?
C
?
A
?
∟
B
C
A
现象:
两个直角三角形能重合。
说明:
当一个直角三角形的一条直角边和
斜边确定后,
那么它的形状和大小
也被确定.
判定公理:
有斜边和一条直角边对应相等的
两个直角三角形全等.
条件1
条件2
前提
斜边和一条直角边对应相等的两个直角三角形全等.
简写:“斜边、直角边”或“HL”
A
B=A?B?
A
C=
A?C?(
或BC=
B?C?)
∴Rt△ABC≌Rt△
A?B?C?(H
L)
直角三角形全等的判定方法:
证明:在Rt△ABC与Rt△
A?B?C?中
通过刚才的探索,发现工作人员的做法
是完全正确的。
