人教版五年级上册数学期末总复习位置、可能性、植树问题课件(15张)
文档属性
| 名称 | 人教版五年级上册数学期末总复习位置、可能性、植树问题课件(15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 12:22:46 | ||
图片预览


文档简介
位置、可能性、植树问题
R·五年级上册
一、复习位置
你们还记得怎样用数对表示位置吗?
用数对表示位置要注意什么问题?
(3,4)与(4,3)有什么不同?
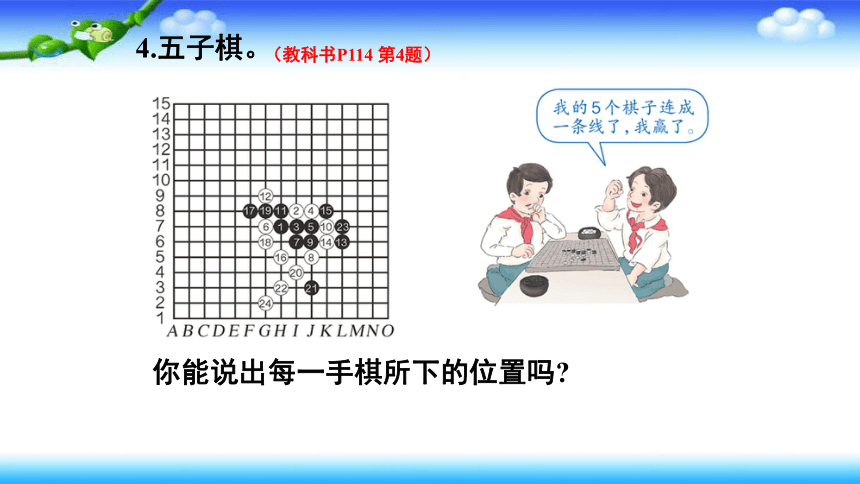
4.五子棋。
(教科书P114 第4题)
你能说出每一手棋所下的位置吗?
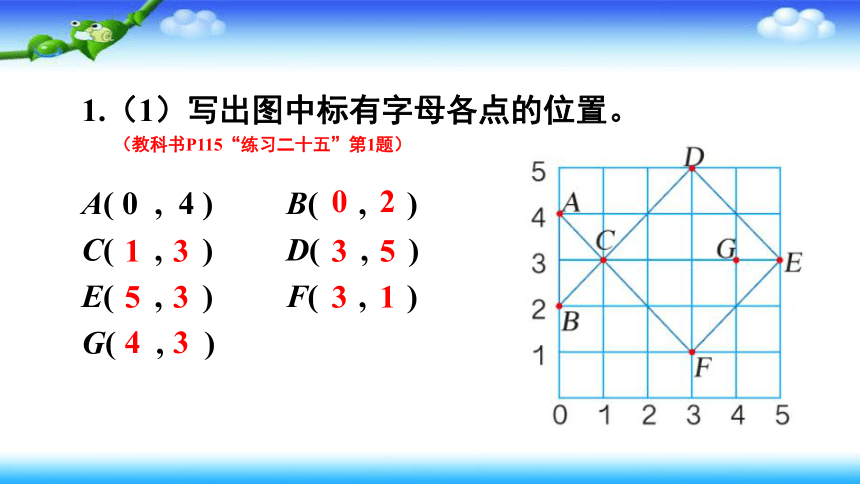
1.(1)写出图中标有字母各点的位置。
A( 0 , 4 ) B( , )
C( , ) D( , )
E( , ) F( , )
G( , )
0 2
1 3
3 5
5 3
3 1
4 3
(教科书P115“练习二十五”第1题)
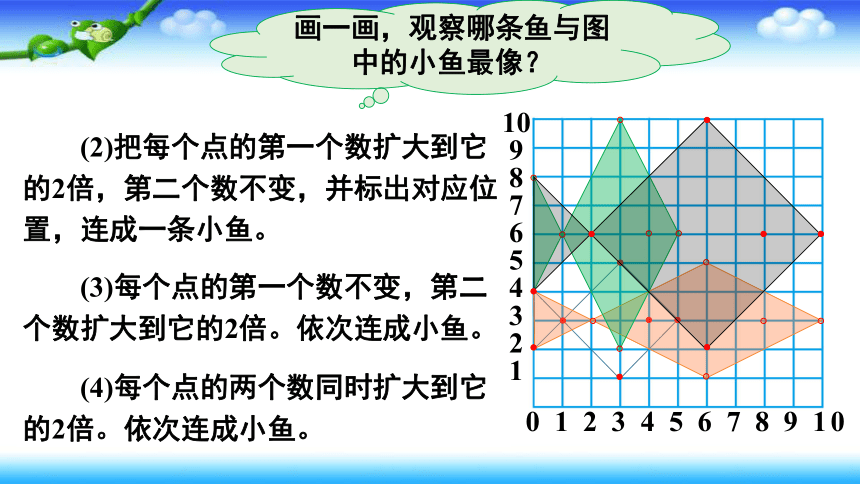
(2)把每个点的第一个数扩大到它的2倍,第二个数不变,并标出对应位置,连成一条小鱼。
(3)每个点的第一个数不变,第二个数扩大到它的2倍。依次连成小鱼。
(4)每个点的两个数同时扩大到它的2倍。依次连成小鱼。
画一画,观察哪条鱼与图中的小鱼最像?
0 1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
请把可能出现的情况填在下面的表格里。
{5940675A-B579-460E-94D1-54222C63F5DA}女孩
男孩
○
√
□
○
○
○
√
√
√
√
□
○
□
□
□
√
○
□
二、复习可能性
5.
(教科书P114第5题)
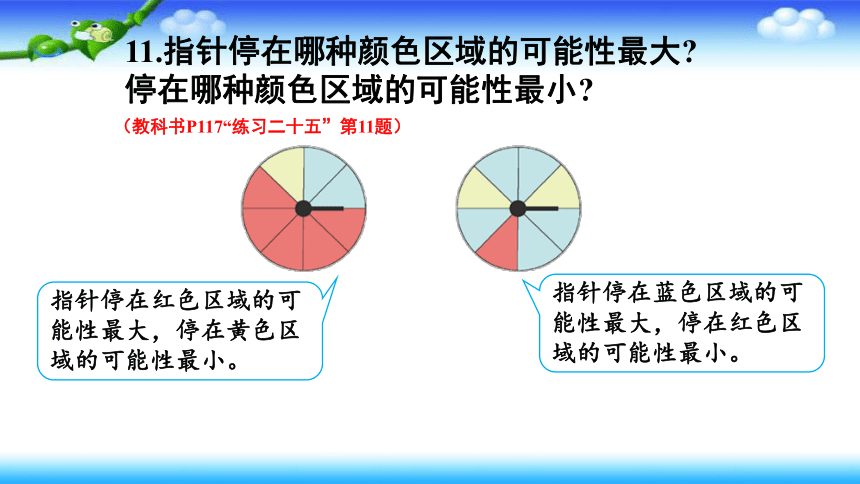
11.指针停在哪种颜色区域的可能性最大?停在哪种颜色区域的可能性最小?
指针停在红色区域的可能性最大,停在黄色区域的可能性最小。
指针停在蓝色区域的可能性最大,停在红色区域的可能性最小。
(教科书P117“练习二十五”第11题)
两个都是正面,两个都是反面,
一个正面一个反面。
12.
(P117“练习二十五”第12题)
三、复习植树问题
常见类型:
①两端都栽的植树问题;
②两端都不栽的植树问题;
③一端栽、一端不栽的植树问题;
④封闭图形的植树问题。
棵数=间隔数+1;
棵数=间隔数-1;
棵数=间隔数;
棵数=间隔数。
在全长20 m的小路上植树,每隔5 m栽一棵,你能想出几种植树方案?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
特点
间隔数
棵树
与间隔数的关系
方案1
两端都栽
方案2
两端都不栽
方案3
一端栽,一端不栽
方案4
封闭图形
4
5
棵树=间隔数+1
4
3
棵树=间隔数-1
4
4
棵树=间隔数
4
4
棵树=间隔数
(1)在一条长400 m的道路一旁安装路灯,每隔50 m安装一座(两端都要安装),一共可以安装多少座路灯?
400÷50=8
间隔数:
8+1=9(座)
可以安装:
答:一共可以安装9座路灯。
(2)两座楼房之间相距56 m,每隔4 m栽雪松一棵,一行能栽多少棵?
56÷4=14
间隔数:
14-1=13(棵)
能栽树:
答:一行能栽13棵。
(3)一个圆形池塘,它的周长是200 m,每隔10 m栽一棵柳树,需要树苗多少棵?
200÷10=20(棵)
间隔数:
答:需要20棵树苗。
四、课堂练习
一座大桥长2400m。一列火车以每分钟900m的速度通过大桥,从车头开上桥到车尾离开桥共需要3分钟。这列火车长多少米?
900×3-2400
=300(m)
答:这列火车长300米。
?备选练习
四、参加武术操表演的运动员站成一个正方形队列。如果使这个正方形队列减少一行和一列,则要减少31人。这个正方形队列最外层共有多少名运动员?参加武术操表演的运动员共有多少名?。
16×4-4=60(名)
(31+1) ÷2=16(名)
16×16=256(名)
答:这个正方形队列最外层共有60名运动员。参加武术操表演的运动员共有256名。
R·五年级上册
一、复习位置
你们还记得怎样用数对表示位置吗?
用数对表示位置要注意什么问题?
(3,4)与(4,3)有什么不同?
4.五子棋。
(教科书P114 第4题)
你能说出每一手棋所下的位置吗?
1.(1)写出图中标有字母各点的位置。
A( 0 , 4 ) B( , )
C( , ) D( , )
E( , ) F( , )
G( , )
0 2
1 3
3 5
5 3
3 1
4 3
(教科书P115“练习二十五”第1题)
(2)把每个点的第一个数扩大到它的2倍,第二个数不变,并标出对应位置,连成一条小鱼。
(3)每个点的第一个数不变,第二个数扩大到它的2倍。依次连成小鱼。
(4)每个点的两个数同时扩大到它的2倍。依次连成小鱼。
画一画,观察哪条鱼与图中的小鱼最像?
0 1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
请把可能出现的情况填在下面的表格里。
{5940675A-B579-460E-94D1-54222C63F5DA}女孩
男孩
○
√
□
○
○
○
√
√
√
√
□
○
□
□
□
√
○
□
二、复习可能性
5.
(教科书P114第5题)
11.指针停在哪种颜色区域的可能性最大?停在哪种颜色区域的可能性最小?
指针停在红色区域的可能性最大,停在黄色区域的可能性最小。
指针停在蓝色区域的可能性最大,停在红色区域的可能性最小。
(教科书P117“练习二十五”第11题)
两个都是正面,两个都是反面,
一个正面一个反面。
12.
(P117“练习二十五”第12题)
三、复习植树问题
常见类型:
①两端都栽的植树问题;
②两端都不栽的植树问题;
③一端栽、一端不栽的植树问题;
④封闭图形的植树问题。
棵数=间隔数+1;
棵数=间隔数-1;
棵数=间隔数;
棵数=间隔数。
在全长20 m的小路上植树,每隔5 m栽一棵,你能想出几种植树方案?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
特点
间隔数
棵树
与间隔数的关系
方案1
两端都栽
方案2
两端都不栽
方案3
一端栽,一端不栽
方案4
封闭图形
4
5
棵树=间隔数+1
4
3
棵树=间隔数-1
4
4
棵树=间隔数
4
4
棵树=间隔数
(1)在一条长400 m的道路一旁安装路灯,每隔50 m安装一座(两端都要安装),一共可以安装多少座路灯?
400÷50=8
间隔数:
8+1=9(座)
可以安装:
答:一共可以安装9座路灯。
(2)两座楼房之间相距56 m,每隔4 m栽雪松一棵,一行能栽多少棵?
56÷4=14
间隔数:
14-1=13(棵)
能栽树:
答:一行能栽13棵。
(3)一个圆形池塘,它的周长是200 m,每隔10 m栽一棵柳树,需要树苗多少棵?
200÷10=20(棵)
间隔数:
答:需要20棵树苗。
四、课堂练习
一座大桥长2400m。一列火车以每分钟900m的速度通过大桥,从车头开上桥到车尾离开桥共需要3分钟。这列火车长多少米?
900×3-2400
=300(m)
答:这列火车长300米。
?备选练习
四、参加武术操表演的运动员站成一个正方形队列。如果使这个正方形队列减少一行和一列,则要减少31人。这个正方形队列最外层共有多少名运动员?参加武术操表演的运动员共有多少名?。
16×4-4=60(名)
(31+1) ÷2=16(名)
16×16=256(名)
答:这个正方形队列最外层共有60名运动员。参加武术操表演的运动员共有256名。
