沪科版(2012)初中数学八年级上 12.2.2 一次函数 正比例函数的图象性质 教案
文档属性
| 名称 | 沪科版(2012)初中数学八年级上 12.2.2 一次函数 正比例函数的图象性质 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 63.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 06:46:24 | ||
图片预览


文档简介
§12.2.1一次函数——正比例函数图象性质
教学目标:
知识与技能
1、认识一次函数和正比例函数的意义,掌握一次函数和正比例函数解析
式的特点;
2、理解正比例函数图象性质及特点;
3、能利用所学知识解决相关实际问题。
方法与过程
1、经历思考、探究过程,发展总结归纳能力,能有条理地、清晰地阐述
自己的观点;
2、体验数形之间的联系,逐步学会利用数形结合思想分析解决相关问题;
情感、态度与价值观
让学生积极参与数学活动,对数学产生兴趣和求知欲,,认识数学与人类
生活的密切联系和对人类历史发展的作用,提高学生参加数学学习活动的积极
性。
教学重点:
1、认识一次函数和正比例函数的意义,掌握一次函数和正比例函数解析
式的特点;
2、理解掌握正比例函数图象的性质特点。
教学难点:
利用正比例函数图象性质解决问题
教学用具:
直尺
多媒体
几何画板
教学过程:
1、复习引入
(1)、函数概念:在一个变化的过程中,存在着两个变量x、y,当x在允许的范围内每取一个值时,y都有唯一一个值与之对应,x叫自变量,y叫因变量,y是x的函数
(2)、函数的表示方法:10列表发;20图象法;30解析式法
(3)、观察下列函数解析式
思考:这几个函数有什么共同特点?
共同特点:1、都含有两个变量;
2、自变量的次数都是一次的;
3、等号的右边都是整式。
2、新课探究
(1)一次函数:一般地,形如y=kx+b(k,b为常数,且
k≠0)的函数叫一次函数
注意:k值一定不能为0!如果k=0会怎样?
b的取值可不可以为零?
(2)正比例函数:一般地,形如y=kx(k为常数,且
k≠0)的函数叫y是x的正比例函数
注意:正比例函数是一次函数y=kx+b当b=0时的特殊形式,
属于一次函数
判断:y=k(x-3);
y=kx2
是否y是x的正比例函数?
思考:正比例的函数图像是什么?怎么画正比例的函数图像?
(3)操作:画正比例函数
y
=2x
的图象
解:1、列表
X
…
-2
-1
0
1
2
…
Y
…
-4
-2
0
2
4
…
2、描点
3、连线
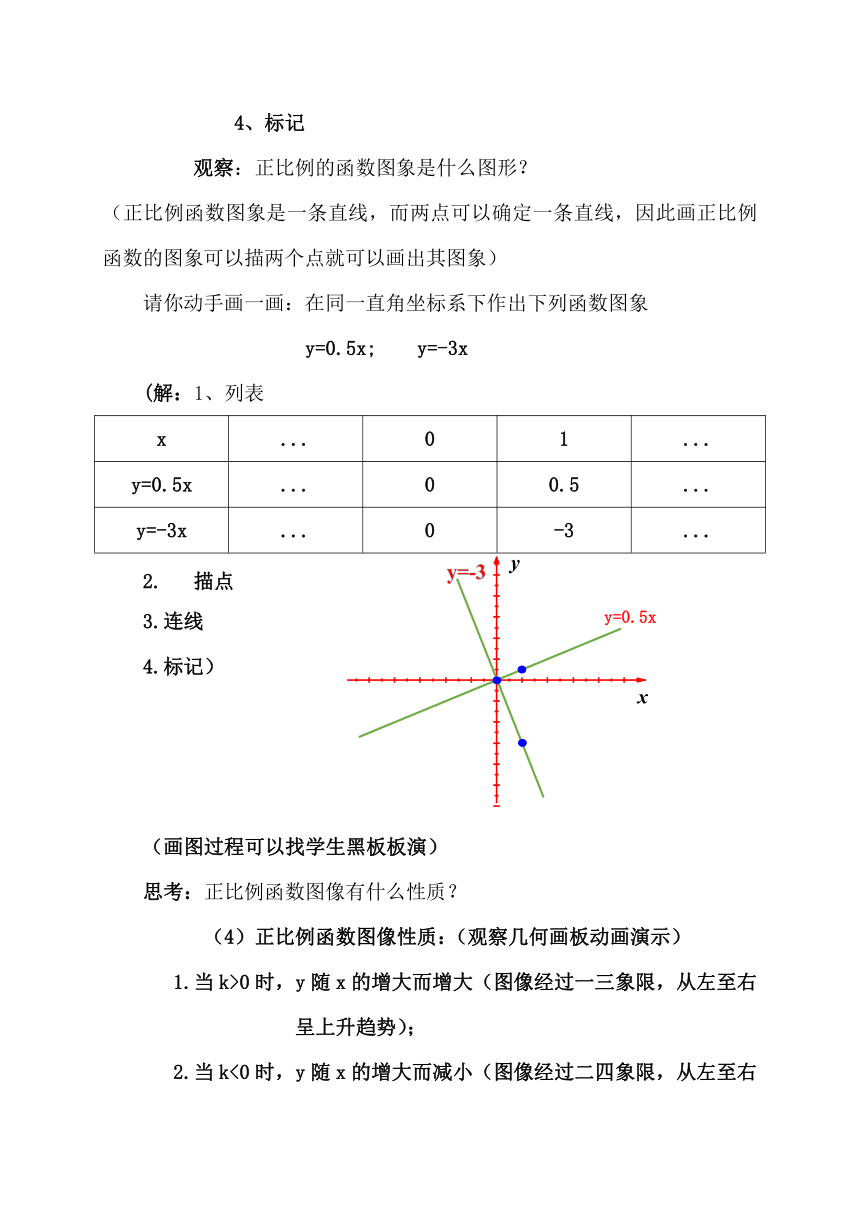
4、标记
观察:正比例的函数图象是什么图形?
(正比例函数图象是一条直线,而两点可以确定一条直线,因此画正比例函数的图象可以描两个点就可以画出其图象)
请你动手画一画:在同一直角坐标系下作出下列函数图象
y=0.5x;
y=-3x
(解:1、列表
x
...
0
1
...
y=0.5x
...
0
0.5
...
y=-3x
...
0
-3
...
描点
连线
标记)
(画图过程可以找学生黑板板演)
思考:正比例函数图像有什么性质?
(4)正比例函数图像性质:(观察几何画板动画演示)
1.当k>0时,y随x的增大而增大(图像经过一三象限,从左至右
呈上升趋势);
2.当k<0时,y随x的增大而减小(图像经过二四象限,从左至右
呈下降趋势);
3.
图像经过定点(0,0);
4.
当|k|越大,图像越靠近y轴,图像走势越陡峭;
当|k|越小,图像越靠近x轴,图像走势越平坦。
正比例函数图象性质表格表示
3、例题解析
例1:已知正比例函数y=kx
(1)若函数图象经过第二、四象限,则k的取值范围是多少?
(2)点(1,-2)在它的图象上,求k的值。
例2、已知正比例函数
的图象经过第一、三象限,
求m的值.
4、练习:1、下列函数中,正比例函数是(
)
A、y=-8x
B、y=-8x+1
C、y=8x2+1
D、
2、
一直正比例函数y=kx(k≠0)的图象经过一、三象限,
那么
(
)
A.k<0
B.k>0
C.k<-2
D.k>2
3、正比例函数y=(m-1)x的图像经过一、三象限,则m的取值范
围是
(
)
A.m=1
B.m>1
C.m<1
D.m≥1
4、正比例函数y=kx图象经过点(1,-4),那么k=____.此函数
图象经过第________象限,函数值y随x的增大而_______.已知点
A(a,1),B(-2,b)在函数图象上,则a=_____,b=_____
5、下列函数y=5x,y=
-3x,
y=
x,y=
x中,y随x的增大而
减小的是____________________,y随x的增大而减小最先达到-10的
是____________
5课堂小结
今天的收获是什么?(正比例函数图象性质,师生共同回顾)
布置作业
作业:在同一坐标系中画出下列函数图象
(1)y=-2x-1;y=-2x;y=-2x+1.
(2)y=3x-1;y=3x;y=3x+1.
7、板书设计
§12.2.1一次函数
——正比例函数图象性质
正比例函数图象性质
1.当k>0时,y随x的增大而增大(图像经过一三象限,从左至右
呈上升趋势);
2.当k<0时,y随x的增大而减小
(图像经过二四象限,从左至右
呈下降趋势);
3.
图像经过定点(0,0);
4.
当|k|越大,图像越靠近y轴,图像走势越陡峭;
当|k|越小,图像越靠近x轴,图像走势越平坦。
多媒体屏幕
8反思:
教学目标:
知识与技能
1、认识一次函数和正比例函数的意义,掌握一次函数和正比例函数解析
式的特点;
2、理解正比例函数图象性质及特点;
3、能利用所学知识解决相关实际问题。
方法与过程
1、经历思考、探究过程,发展总结归纳能力,能有条理地、清晰地阐述
自己的观点;
2、体验数形之间的联系,逐步学会利用数形结合思想分析解决相关问题;
情感、态度与价值观
让学生积极参与数学活动,对数学产生兴趣和求知欲,,认识数学与人类
生活的密切联系和对人类历史发展的作用,提高学生参加数学学习活动的积极
性。
教学重点:
1、认识一次函数和正比例函数的意义,掌握一次函数和正比例函数解析
式的特点;
2、理解掌握正比例函数图象的性质特点。
教学难点:
利用正比例函数图象性质解决问题
教学用具:
直尺
多媒体
几何画板
教学过程:
1、复习引入
(1)、函数概念:在一个变化的过程中,存在着两个变量x、y,当x在允许的范围内每取一个值时,y都有唯一一个值与之对应,x叫自变量,y叫因变量,y是x的函数
(2)、函数的表示方法:10列表发;20图象法;30解析式法
(3)、观察下列函数解析式
思考:这几个函数有什么共同特点?
共同特点:1、都含有两个变量;
2、自变量的次数都是一次的;
3、等号的右边都是整式。
2、新课探究
(1)一次函数:一般地,形如y=kx+b(k,b为常数,且
k≠0)的函数叫一次函数
注意:k值一定不能为0!如果k=0会怎样?
b的取值可不可以为零?
(2)正比例函数:一般地,形如y=kx(k为常数,且
k≠0)的函数叫y是x的正比例函数
注意:正比例函数是一次函数y=kx+b当b=0时的特殊形式,
属于一次函数
判断:y=k(x-3);
y=kx2
是否y是x的正比例函数?
思考:正比例的函数图像是什么?怎么画正比例的函数图像?
(3)操作:画正比例函数
y
=2x
的图象
解:1、列表
X
…
-2
-1
0
1
2
…
Y
…
-4
-2
0
2
4
…
2、描点
3、连线
4、标记
观察:正比例的函数图象是什么图形?
(正比例函数图象是一条直线,而两点可以确定一条直线,因此画正比例函数的图象可以描两个点就可以画出其图象)
请你动手画一画:在同一直角坐标系下作出下列函数图象
y=0.5x;
y=-3x
(解:1、列表
x
...
0
1
...
y=0.5x
...
0
0.5
...
y=-3x
...
0
-3
...
描点
连线
标记)
(画图过程可以找学生黑板板演)
思考:正比例函数图像有什么性质?
(4)正比例函数图像性质:(观察几何画板动画演示)
1.当k>0时,y随x的增大而增大(图像经过一三象限,从左至右
呈上升趋势);
2.当k<0时,y随x的增大而减小(图像经过二四象限,从左至右
呈下降趋势);
3.
图像经过定点(0,0);
4.
当|k|越大,图像越靠近y轴,图像走势越陡峭;
当|k|越小,图像越靠近x轴,图像走势越平坦。
正比例函数图象性质表格表示
3、例题解析
例1:已知正比例函数y=kx
(1)若函数图象经过第二、四象限,则k的取值范围是多少?
(2)点(1,-2)在它的图象上,求k的值。
例2、已知正比例函数
的图象经过第一、三象限,
求m的值.
4、练习:1、下列函数中,正比例函数是(
)
A、y=-8x
B、y=-8x+1
C、y=8x2+1
D、
2、
一直正比例函数y=kx(k≠0)的图象经过一、三象限,
那么
(
)
A.k<0
B.k>0
C.k<-2
D.k>2
3、正比例函数y=(m-1)x的图像经过一、三象限,则m的取值范
围是
(
)
A.m=1
B.m>1
C.m<1
D.m≥1
4、正比例函数y=kx图象经过点(1,-4),那么k=____.此函数
图象经过第________象限,函数值y随x的增大而_______.已知点
A(a,1),B(-2,b)在函数图象上,则a=_____,b=_____
5、下列函数y=5x,y=
-3x,
y=
x,y=
x中,y随x的增大而
减小的是____________________,y随x的增大而减小最先达到-10的
是____________
5课堂小结
今天的收获是什么?(正比例函数图象性质,师生共同回顾)
布置作业
作业:在同一坐标系中画出下列函数图象
(1)y=-2x-1;y=-2x;y=-2x+1.
(2)y=3x-1;y=3x;y=3x+1.
7、板书设计
§12.2.1一次函数
——正比例函数图象性质
正比例函数图象性质
1.当k>0时,y随x的增大而增大(图像经过一三象限,从左至右
呈上升趋势);
2.当k<0时,y随x的增大而减小
(图像经过二四象限,从左至右
呈下降趋势);
3.
图像经过定点(0,0);
4.
当|k|越大,图像越靠近y轴,图像走势越陡峭;
当|k|越小,图像越靠近x轴,图像走势越平坦。
多媒体屏幕
8反思:
