沪科版(2012)初中数学八年级上 12.2.2 正比例函数的图像和性质 教案
文档属性
| 名称 | 沪科版(2012)初中数学八年级上 12.2.2 正比例函数的图像和性质 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 600.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 06:44:55 | ||
图片预览



文档简介
正比例函数的图像和性质教学设计
教学目标:
知识与技能:
(1)能画正比例函数的图像,并能结合公理和正比例函数图象特点快速作图;
(2)能够在画图过程中观察并发现函数的性质;学会简单描述及应用。
过程与方法:
(1)初步能够从数学角度去观察事物,思考问题,体验解决问题方法策略的多样性;
(2)逐步培养学生的观察能力,概括的能力,通过教师指导发现知识,初步培养学生数形结合的思想以及由特殊到一般的数学思想;
(3)能够尝试演绎推理发现规律,体验合作学习的过程。
情感态度与价值观:
(1)通过小组合做讨论,鼓励学生从多角度思考、探索、交流,激发学生的好奇心和主动学习的欲望;
(2)通过本节课的教学希望能激发学生学习数学的兴趣和积极性,逐步培养学生实事求是的科学态度。
二、设计意图与教法:四环节
1、学生先自学P87例1中y=2x的画法,然后独立在同一直角坐标系中画出y=2x,y=-2x的图象。再通过观察、发现两图象的共性,得到正比例函数的图象是一条经过原点的直线,并根据图象特点找到正比例函数图象的简单作法:
两点法:(0,0)(1,k)。
2、自学阅读理解P89,小组合作完成探究题1,2交流、梳理、归纳出正比例函数图象的象限、增减性和k的正负性的关系。
3、完成检测,进一步加深理解正比例函数图象性质,并解决相关问题的。
4、拓展提升正比例函数图象性质,关于x轴、y轴对称,k互为相反数。K的绝对值越大,图象越靠近
y轴。
三、学习方法
画图:在同一直角坐标系中参照P87例1画出y=2x,y=-2x,两点法画出y
=
-
3x,
y
=
-
x,
y
=
3x,
y
=
x。
观察:观察两次的画图中的图象相同和不同。
归纳:根据观察、交流、归纳出正比例函数图象性质。
运用:简单运用和拓展练习。
教学过程:
一、复习引入、温故知新
1.正比例函数的定义
一般地,形如
y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
2.画函数图象的步骤
列表、描点、连线
【设计意图】:这样的设计,适合学生的学习习惯,能让学生在温习旧知识的过程中体验会旧知与新知之间的联系,积极探索新知识。
二、出示学习目标:
1、能画正比例函数的图象,并能结合公理和正比例函数图象特点快速作图;
2、能够在画图过程中观察并发现函数的性质;学会简单描述及应用。
重点:画正比例函数的图象,并在画图过程中观察并发现函数的性质。
难点:在画图过程中观察并发现函数的性质;学会简单描述及应用。
【设计意图】:明确这节课要学习的目标和重、难点。
三、自学指导一(自主学习)
参照P87例1中y=2x的画法,在同一直角坐标系中画出正比例函数y=2x,y=-2x的图象。
思考:1、观察正比例函数的图象是什么?
2、你能快速作图吗?
探究正比例函数的图象
(一)
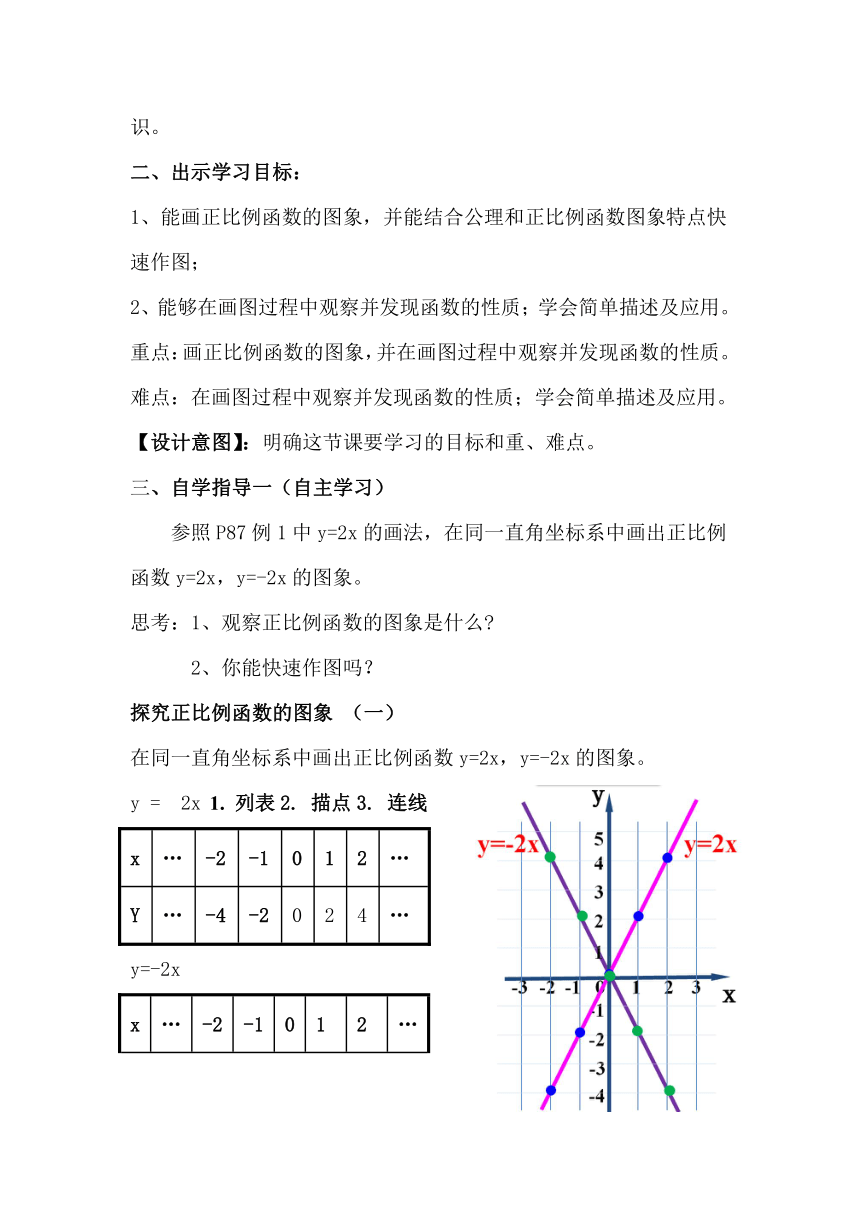
在同一直角坐标系中画出正比例函数y=2x,y=-2x的图象。
y
=
2x
1.
列表2.
描点3.
连线
x
…
-2
-1
0
1
2
…
Y
…
-4
-2
0
2
4
…
y=-2x
x
…
-2
-1
0
1
2
…
Y
…
4
2
0
-2
-4
…
1、
你发现正比例函数的图象特征是什么?
正比例函数的图象是一条经过原点的直线,我们称它为直线y=kx。
2、
根据正比例函数图象特点你能快速作图?
正比例函数图象的简单作法:
两点法:(0,0)(1,k)
【设计意图】:这样的设计,主要是让学生更多熟悉数与形的结合,体会数到形的转变,还为下一步的的探究做好辅垫。经历动手画图,熟练画图步骤,通过观察图象特征,组内交流得出正比例函数的图象是一条经过原点的直线的直线。引导学生根据公理:两点确定一条直线,得到正比例函数图象的简单作图方法:两点法:(0,0)(1,k)。达到学习目标2,把握重点,突破难点。
四、检测一
:
1、
在上同一直角坐标系中用两点法快速画出正比例函数
y
=
-
3x,
y
=
-
x,
y
=
3x,
y
=
x的图象。
y
=
-
3x
y
=
-
x
y
=
3x
y
=
x
【设计意图】:练习运用两点法快速作正比例函数图象。体会两点法画图的便捷及加深理解正比例函数图象特征。熟练学习目标1.
五、自学指导二(合作学习)
阅读书P89思考以上的部分。
1、完成探究二第1题,思考由第1题可以得到正比例函数的图象经过什么象限?
2、完成第2题,思考由第2题可以得到正比例函数的图象y随x如何变化?
探究正比例函数的图象性质(二)
1、(1)观察正比例函数y
=
-
3x,
y
=
-2
x,
y
=
-
x图象经过第
象限,
K
0;
(2)观察正比例函数y
=
3x,
y
=
2x,y
=
x图象经过第
象限,
K
0;
(3)由(1)、(2)可知道正比例函数图象的位置由
确定。
结论:
(1)当k>0时,直线y=kx经过一、三象限;
(2)当k<0时,直线y=kx经过二、四象限。
【设计意图】:经历观察检测一中画的图象,完成探究题1,容易梳理归纳出正比例函数图象的象限和k的正负性的关系。达到学习目标2,把握重点,突破难点。
2、从左向右看,观察正比例函数y=2x的图象从左向右
,随着x的增大,
y
,k
0
;
y=-2x的图象从左向右
,随着x的增大,
y
,k
0
。
结论:
(1)当k
>
0时,
y随x的增大而增大。
(2)当k
<
0时,
y随x的增大而减小。
【设计意图】:经历观察检测一中画的图象,完成探究题,容易梳理归纳出正比例函数图象的增减性和k的正负性的关系。达到学习目标2,把握重点,突破难点。
六、检测二
:
1、
下列正比函数中,y随x增大而减小的有________;y随x增大而增大
的有________.
2、正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是
(
)
A.m=1
B.m>1
C.m<1
D.m≥1
3、如果函数y=kx-(2-k)的图像过原点的一条直线,那么K=______。
【设计意图】:通过完成检测二,检测和巩固学习目标2。
七、拓展提升
:
1、(1)观察正比例函数y
=
-
3x与y
=
3x
,
y
=
-2
x
与y
=
2x,
y
=
-x与y
=
x
的位置关于
对称,比例系数K的关系是
。
(2)当
越大时,图象越靠近
y轴。
【设计意图】:经历观察检测一中画的图象,完成拓展提升
,容易梳理归纳出两正比例函数图象关于x轴、y轴对称,k互为相反数。K的绝对值越大,图象越靠近
y轴,是对学习目标2的一个补充,并对这节课知识的一个提升和拓展。
八、课堂小结
:
九、布置作业:点拨
板书设计:
19.2.1
正比例函数的图象与性质
十、教学反思
教学设计中由复习引入,适合学生的学习习惯,能让学生在温习旧知识的过程中体验会旧知与新知之间的联系,积极探索新知识。经历动手画图,通过观察图象特征,组内交流得出正比例函数的图象,得到正比例函数图象的简单作图方法:两点法达到学习目标1、2,把握重点,突破难点。通过检测,及时巩固学习目标1、2。经历观察检测一中画的图象,完成拓展提升
,归纳出两正比例函数图象关于x轴、y轴对称,k互为相反数。K的绝对值越大,图象越靠近
y轴,是对学习目标2的一个补充,并对这节课知识的一个提升和拓展。
每一步完成的比较实,达到到了学习的目标。
不足之处:在探究正比例函数的图象与性质中,应在画出y
=
-2
x
与y
=
2x两条直线时观察图象,根据图形异同点一次性把书上涉及到的性质都总结出来,不应该分两次探究,这样一是设计不紧凑,二是只有两条直线便于观察。
教学目标:
知识与技能:
(1)能画正比例函数的图像,并能结合公理和正比例函数图象特点快速作图;
(2)能够在画图过程中观察并发现函数的性质;学会简单描述及应用。
过程与方法:
(1)初步能够从数学角度去观察事物,思考问题,体验解决问题方法策略的多样性;
(2)逐步培养学生的观察能力,概括的能力,通过教师指导发现知识,初步培养学生数形结合的思想以及由特殊到一般的数学思想;
(3)能够尝试演绎推理发现规律,体验合作学习的过程。
情感态度与价值观:
(1)通过小组合做讨论,鼓励学生从多角度思考、探索、交流,激发学生的好奇心和主动学习的欲望;
(2)通过本节课的教学希望能激发学生学习数学的兴趣和积极性,逐步培养学生实事求是的科学态度。
二、设计意图与教法:四环节
1、学生先自学P87例1中y=2x的画法,然后独立在同一直角坐标系中画出y=2x,y=-2x的图象。再通过观察、发现两图象的共性,得到正比例函数的图象是一条经过原点的直线,并根据图象特点找到正比例函数图象的简单作法:
两点法:(0,0)(1,k)。
2、自学阅读理解P89,小组合作完成探究题1,2交流、梳理、归纳出正比例函数图象的象限、增减性和k的正负性的关系。
3、完成检测,进一步加深理解正比例函数图象性质,并解决相关问题的。
4、拓展提升正比例函数图象性质,关于x轴、y轴对称,k互为相反数。K的绝对值越大,图象越靠近
y轴。
三、学习方法
画图:在同一直角坐标系中参照P87例1画出y=2x,y=-2x,两点法画出y
=
-
3x,
y
=
-
x,
y
=
3x,
y
=
x。
观察:观察两次的画图中的图象相同和不同。
归纳:根据观察、交流、归纳出正比例函数图象性质。
运用:简单运用和拓展练习。
教学过程:
一、复习引入、温故知新
1.正比例函数的定义
一般地,形如
y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
2.画函数图象的步骤
列表、描点、连线
【设计意图】:这样的设计,适合学生的学习习惯,能让学生在温习旧知识的过程中体验会旧知与新知之间的联系,积极探索新知识。
二、出示学习目标:
1、能画正比例函数的图象,并能结合公理和正比例函数图象特点快速作图;
2、能够在画图过程中观察并发现函数的性质;学会简单描述及应用。
重点:画正比例函数的图象,并在画图过程中观察并发现函数的性质。
难点:在画图过程中观察并发现函数的性质;学会简单描述及应用。
【设计意图】:明确这节课要学习的目标和重、难点。
三、自学指导一(自主学习)
参照P87例1中y=2x的画法,在同一直角坐标系中画出正比例函数y=2x,y=-2x的图象。
思考:1、观察正比例函数的图象是什么?
2、你能快速作图吗?
探究正比例函数的图象
(一)
在同一直角坐标系中画出正比例函数y=2x,y=-2x的图象。
y
=
2x
1.
列表2.
描点3.
连线
x
…
-2
-1
0
1
2
…
Y
…
-4
-2
0
2
4
…
y=-2x
x
…
-2
-1
0
1
2
…
Y
…
4
2
0
-2
-4
…
1、
你发现正比例函数的图象特征是什么?
正比例函数的图象是一条经过原点的直线,我们称它为直线y=kx。
2、
根据正比例函数图象特点你能快速作图?
正比例函数图象的简单作法:
两点法:(0,0)(1,k)
【设计意图】:这样的设计,主要是让学生更多熟悉数与形的结合,体会数到形的转变,还为下一步的的探究做好辅垫。经历动手画图,熟练画图步骤,通过观察图象特征,组内交流得出正比例函数的图象是一条经过原点的直线的直线。引导学生根据公理:两点确定一条直线,得到正比例函数图象的简单作图方法:两点法:(0,0)(1,k)。达到学习目标2,把握重点,突破难点。
四、检测一
:
1、
在上同一直角坐标系中用两点法快速画出正比例函数
y
=
-
3x,
y
=
-
x,
y
=
3x,
y
=
x的图象。
y
=
-
3x
y
=
-
x
y
=
3x
y
=
x
【设计意图】:练习运用两点法快速作正比例函数图象。体会两点法画图的便捷及加深理解正比例函数图象特征。熟练学习目标1.
五、自学指导二(合作学习)
阅读书P89思考以上的部分。
1、完成探究二第1题,思考由第1题可以得到正比例函数的图象经过什么象限?
2、完成第2题,思考由第2题可以得到正比例函数的图象y随x如何变化?
探究正比例函数的图象性质(二)
1、(1)观察正比例函数y
=
-
3x,
y
=
-2
x,
y
=
-
x图象经过第
象限,
K
0;
(2)观察正比例函数y
=
3x,
y
=
2x,y
=
x图象经过第
象限,
K
0;
(3)由(1)、(2)可知道正比例函数图象的位置由
确定。
结论:
(1)当k>0时,直线y=kx经过一、三象限;
(2)当k<0时,直线y=kx经过二、四象限。
【设计意图】:经历观察检测一中画的图象,完成探究题1,容易梳理归纳出正比例函数图象的象限和k的正负性的关系。达到学习目标2,把握重点,突破难点。
2、从左向右看,观察正比例函数y=2x的图象从左向右
,随着x的增大,
y
,k
0
;
y=-2x的图象从左向右
,随着x的增大,
y
,k
0
。
结论:
(1)当k
>
0时,
y随x的增大而增大。
(2)当k
<
0时,
y随x的增大而减小。
【设计意图】:经历观察检测一中画的图象,完成探究题,容易梳理归纳出正比例函数图象的增减性和k的正负性的关系。达到学习目标2,把握重点,突破难点。
六、检测二
:
1、
下列正比函数中,y随x增大而减小的有________;y随x增大而增大
的有________.
2、正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是
(
)
A.m=1
B.m>1
C.m<1
D.m≥1
3、如果函数y=kx-(2-k)的图像过原点的一条直线,那么K=______。
【设计意图】:通过完成检测二,检测和巩固学习目标2。
七、拓展提升
:
1、(1)观察正比例函数y
=
-
3x与y
=
3x
,
y
=
-2
x
与y
=
2x,
y
=
-x与y
=
x
的位置关于
对称,比例系数K的关系是
。
(2)当
越大时,图象越靠近
y轴。
【设计意图】:经历观察检测一中画的图象,完成拓展提升
,容易梳理归纳出两正比例函数图象关于x轴、y轴对称,k互为相反数。K的绝对值越大,图象越靠近
y轴,是对学习目标2的一个补充,并对这节课知识的一个提升和拓展。
八、课堂小结
:
九、布置作业:点拨
板书设计:
19.2.1
正比例函数的图象与性质
十、教学反思
教学设计中由复习引入,适合学生的学习习惯,能让学生在温习旧知识的过程中体验会旧知与新知之间的联系,积极探索新知识。经历动手画图,通过观察图象特征,组内交流得出正比例函数的图象,得到正比例函数图象的简单作图方法:两点法达到学习目标1、2,把握重点,突破难点。通过检测,及时巩固学习目标1、2。经历观察检测一中画的图象,完成拓展提升
,归纳出两正比例函数图象关于x轴、y轴对称,k互为相反数。K的绝对值越大,图象越靠近
y轴,是对学习目标2的一个补充,并对这节课知识的一个提升和拓展。
每一步完成的比较实,达到到了学习的目标。
不足之处:在探究正比例函数的图象与性质中,应在画出y
=
-2
x
与y
=
2x两条直线时观察图象,根据图形异同点一次性把书上涉及到的性质都总结出来,不应该分两次探究,这样一是设计不紧凑,二是只有两条直线便于观察。
