期中综合复习测试-沪教版(上海)八年级数学第一学期同步练习
文档属性
| 名称 | 期中综合复习测试-沪教版(上海)八年级数学第一学期同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 101.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 06:42:30 | ||
图片预览


文档简介
期中测试
选择题(每小题3分,共18分)
下列二次根式中是最简二次根式的是(
).
(A)
B
C
D
在下列二次根式中,与是同类二次根式的是(
).
A
B
C
D
3.方程x
2
-5x-1=0的根的情况是
(
).
(A)有两个不相等实根
(B)有两个相等实根
(C)没有实数根
(D)无法确定
4.的有理化因式是(
)
(A)
(B)
(C)
(D)
5.若,则a的取值范围是(?
???)
(A)?
(B)?
(C)?
(D)一切实数
6.如果反比例函数在每个象限内,y随x的增大而减小,那么它的图象分布在(??
??)
(A)?第一.二象限
(B)?第一.三象限
(C)?第二.三象限
(D)第二.四象限
填空题(每小题2分,共26分)
7.函数的定义域是__________.
8.若,则x=_______.
9.比较大小:______.
10.化简(x>0)得________.
11.若关于x的方程有两个实数根,则k的取值范围是________.
12.当x=_______时,代数式和的值互为相反数.
13.在实数范围内因式分解:=_________.
14.如果正比例函数的图像经过第二.四象限,那么k的取值是_________.
15.已知y+3与x成反比例,当x=2时,y=3,则y关于x的函数解析式为___________.
16.上海玩具厂2008年1月份生产玩具3000个,后来生产效率逐月提高,3月份生产玩具3630个,设平均每月增长率为x,则可列方程___________________.
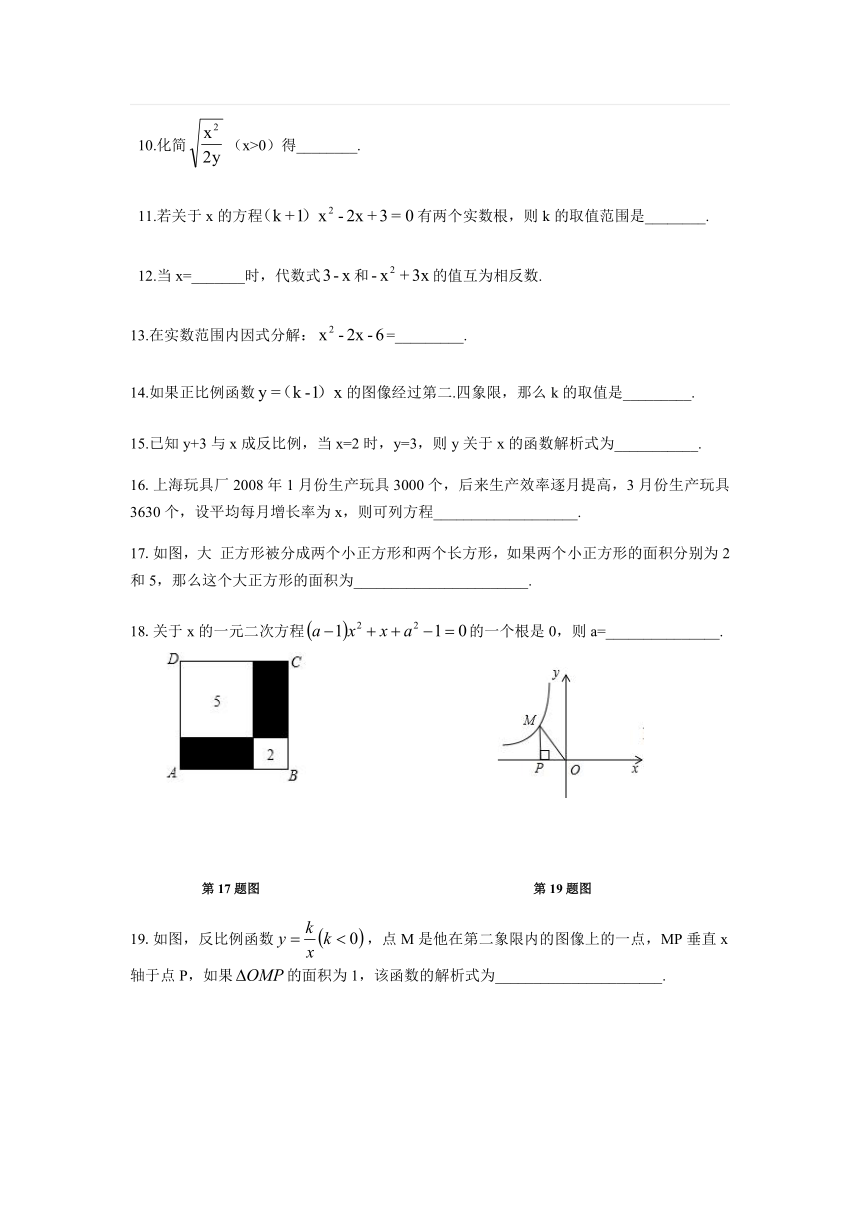
17.如图,大
正方形被分成两个小正方形和两个长方形,如果两个小正方形的面积分别为2和5,那么这个大正方形的面积为_______________________.
18.关于x的一元二次方程的一个根是0,则a=_______________.
第17题图
第19题图
19.如图,反比例函数,点M是他在第二象限内的图像上的一点,MP垂直x轴于点P,如果的面积为1,该函数的解析式为______________________.
三、计算题
20.计算:.
21.化简:.
22.配方法解方程.
23.解方程
四、解答题
24.解不等式:.
25.已知关于x的方程有两个相等的实数根,求k的值并解方程.
26.已知反比例函数与正比例函数相交于点A,点A的坐标是(1,m),求正比例函数解析式.
27.某便利店一月份销售额为20万元,二、三月份稳步增长,一季度销售额共72.8万元,求二、三月份的平均增长率.
28.将进货单价为100元的商品按120元售出时,能卖出500件,已知这种商品每涨1元,其销售量就减少10件.如果希望能够获得利润12000元,售价应定多少元?这时应进货多少件?
29.已知矩形OABC的顶点B(m,2)在正比例函数的图像上,点A在x轴上,点C在y轴上,反比例函数的图像与BC边相交于点K,与AB边交于N,且BK=3CK,求反比例函数解析式及点N的坐标.
参考答案
期中测试
1.D
2.C
3.A
4.A
5.B
6.B
7.
8.16
9.>
10.
11.
12.-1或3
13.
14.k<1
15.
16.
17.
18.-1
19.
20.
21.
22.
23.
24.由于,则,两边同除以-1得,即,两边同除以得,即,亦即
25.,原方程的解为
26.
27.设二、三月份的平均增长率为x,有题意列方程得,解得(舍)。答:二、三月份的平均增长率为20%
28.设每种商品涨x元,原来每件利润120-100=20元。由题意列方程得,解得,当x=10时,120+10=130,500-100=400;当x=20时120+20=140,500-200=300.答:每件定价130元时,应进货400件;或每件定价140元,应进货300件,都可以获得利润12000元
29.将(m,2)带入,得,解得m=4,从而点B(4,2).又因为BK=3CK,所以CK=1,BK=3,从而点K(1,2)所以反比例函数的解析式为,设点N的坐标为N(4,y)代入,解得,所以点N的坐标为N()
选择题(每小题3分,共18分)
下列二次根式中是最简二次根式的是(
).
(A)
B
C
D
在下列二次根式中,与是同类二次根式的是(
).
A
B
C
D
3.方程x
2
-5x-1=0的根的情况是
(
).
(A)有两个不相等实根
(B)有两个相等实根
(C)没有实数根
(D)无法确定
4.的有理化因式是(
)
(A)
(B)
(C)
(D)
5.若,则a的取值范围是(?
???)
(A)?
(B)?
(C)?
(D)一切实数
6.如果反比例函数在每个象限内,y随x的增大而减小,那么它的图象分布在(??
??)
(A)?第一.二象限
(B)?第一.三象限
(C)?第二.三象限
(D)第二.四象限
填空题(每小题2分,共26分)
7.函数的定义域是__________.
8.若,则x=_______.
9.比较大小:______.
10.化简(x>0)得________.
11.若关于x的方程有两个实数根,则k的取值范围是________.
12.当x=_______时,代数式和的值互为相反数.
13.在实数范围内因式分解:=_________.
14.如果正比例函数的图像经过第二.四象限,那么k的取值是_________.
15.已知y+3与x成反比例,当x=2时,y=3,则y关于x的函数解析式为___________.
16.上海玩具厂2008年1月份生产玩具3000个,后来生产效率逐月提高,3月份生产玩具3630个,设平均每月增长率为x,则可列方程___________________.
17.如图,大
正方形被分成两个小正方形和两个长方形,如果两个小正方形的面积分别为2和5,那么这个大正方形的面积为_______________________.
18.关于x的一元二次方程的一个根是0,则a=_______________.
第17题图
第19题图
19.如图,反比例函数,点M是他在第二象限内的图像上的一点,MP垂直x轴于点P,如果的面积为1,该函数的解析式为______________________.
三、计算题
20.计算:.
21.化简:.
22.配方法解方程.
23.解方程
四、解答题
24.解不等式:.
25.已知关于x的方程有两个相等的实数根,求k的值并解方程.
26.已知反比例函数与正比例函数相交于点A,点A的坐标是(1,m),求正比例函数解析式.
27.某便利店一月份销售额为20万元,二、三月份稳步增长,一季度销售额共72.8万元,求二、三月份的平均增长率.
28.将进货单价为100元的商品按120元售出时,能卖出500件,已知这种商品每涨1元,其销售量就减少10件.如果希望能够获得利润12000元,售价应定多少元?这时应进货多少件?
29.已知矩形OABC的顶点B(m,2)在正比例函数的图像上,点A在x轴上,点C在y轴上,反比例函数的图像与BC边相交于点K,与AB边交于N,且BK=3CK,求反比例函数解析式及点N的坐标.
参考答案
期中测试
1.D
2.C
3.A
4.A
5.B
6.B
7.
8.16
9.>
10.
11.
12.-1或3
13.
14.k<1
15.
16.
17.
18.-1
19.
20.
21.
22.
23.
24.由于,则,两边同除以-1得,即,两边同除以得,即,亦即
25.,原方程的解为
26.
27.设二、三月份的平均增长率为x,有题意列方程得,解得(舍)。答:二、三月份的平均增长率为20%
28.设每种商品涨x元,原来每件利润120-100=20元。由题意列方程得,解得,当x=10时,120+10=130,500-100=400;当x=20时120+20=140,500-200=300.答:每件定价130元时,应进货400件;或每件定价140元,应进货300件,都可以获得利润12000元
29.将(m,2)带入,得,解得m=4,从而点B(4,2).又因为BK=3CK,所以CK=1,BK=3,从而点K(1,2)所以反比例函数的解析式为,设点N的坐标为N(4,y)代入,解得,所以点N的坐标为N()
同课章节目录
