人教版八年级数学上册 12.2三角形全等的判定(HL)课件(共13张PPT)
文档属性
| 名称 | 人教版八年级数学上册 12.2三角形全等的判定(HL)课件(共13张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
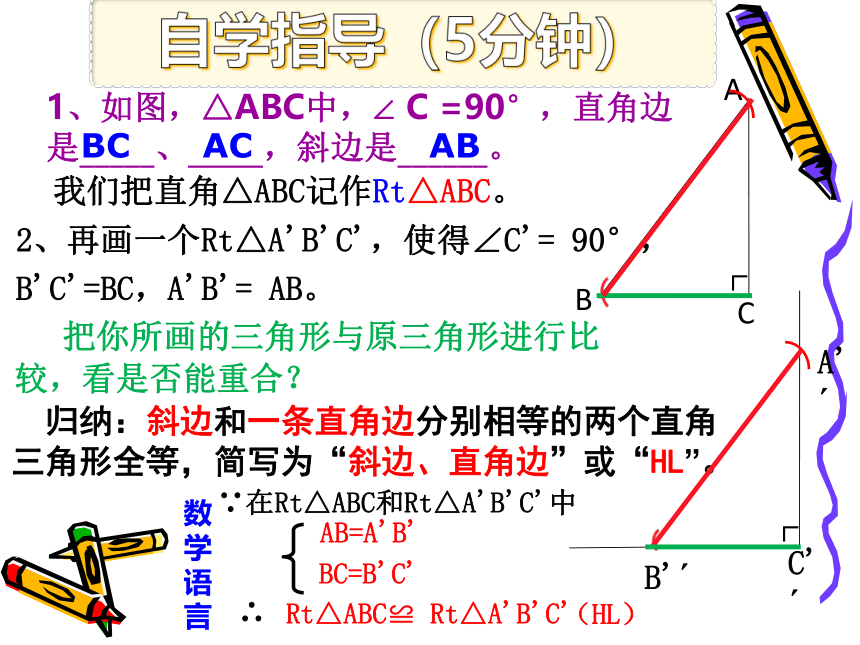
1、判定两个三角形全等方法
,
,
,
。
SSS
ASA
AAS
SAS
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
以上的四种判别三角形全等的方法能不能用来判别Rt△全等呢?
C
B
A
12.2.4
三角形全等的判定
(HL)
学习目标(1分钟)
1、掌握判定直角三角形全等的一种
特殊方法——“斜边、直角边”
(即“HL”).
2、能熟练地用判定一般三角形全等的
方法及判定直角三角形全等的特殊
方法来判定两个直角三角形全等.
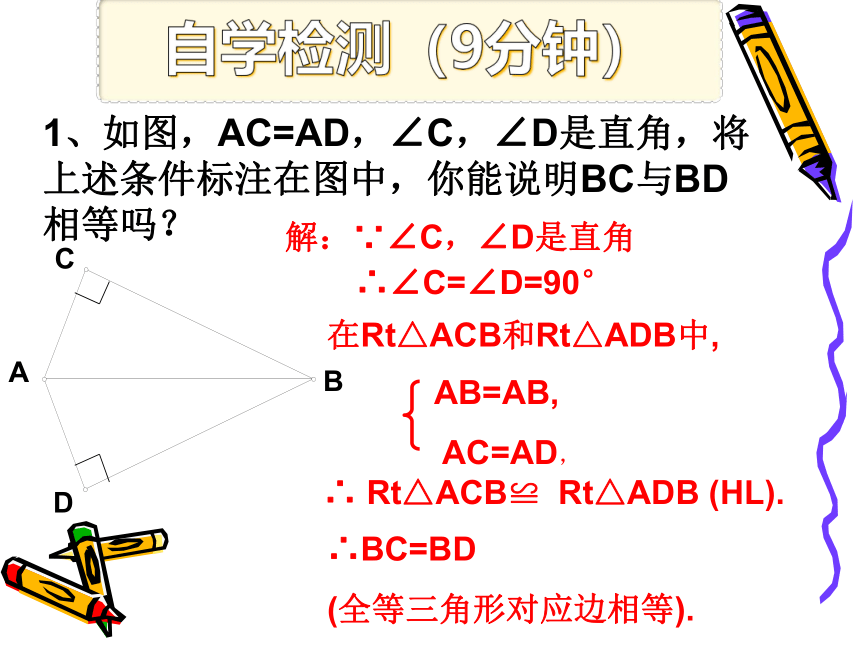
自学指导(5分钟)
1、如图,△ABC中,∠
C
=90°,直角边是_____、_____,斜边是______。
我们把直角△ABC记作Rt△ABC。
AC
BC
AB
∟
B
C
A
∟
C'?
2、再画一个Rt△A'B'C',使得∠C'=
90°,
B'C'=BC,A'B'=
AB。
A'?
B'?
把你所画的三角形与原三角形进行比较,看是否能重合?
归纳:斜边和一条直角边分别相等的两个直角三角形全等,简写为“斜边、直角边”或“HL”。
AB=A'B'
∵在Rt△ABC和Rt△A'B'C'中
Rt△ABC≌
Rt△A'B'C'
∴
(HL)
BC=B'C'
数
学
语
言
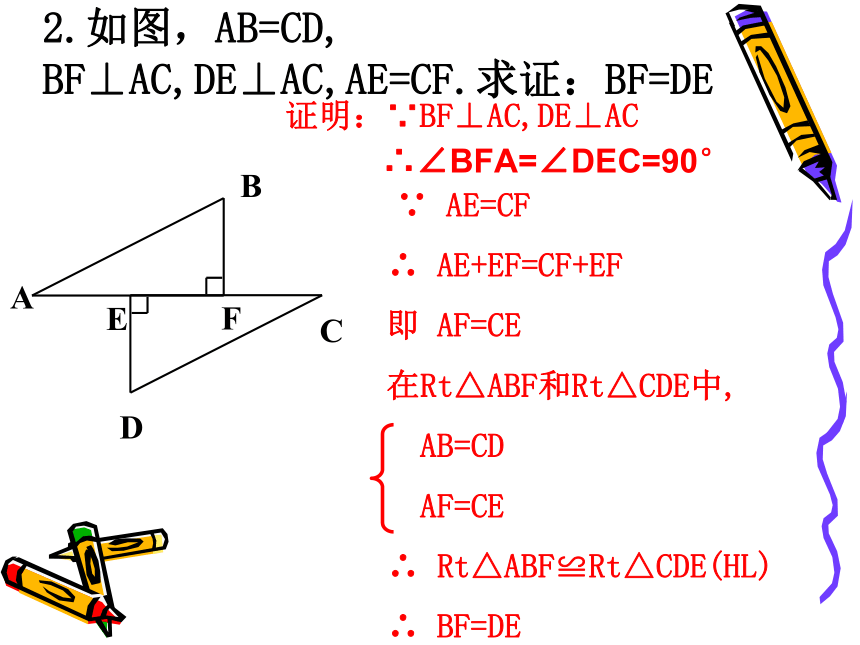
自学检测(9分钟)
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
在Rt△ACB和Rt△ADB中,
AB=AB,
AC=AD,
∴
Rt△ACB≌
Rt△ADB
(HL).
∴BC=BD
(全等三角形对应边相等).
解:∵∠C,∠D是直角
∴∠C=∠D=90°
A
F
C
E
D
B
2.如图,AB=CD,
BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE
∵
AE=CF
∴
AE+EF=CF+EF
即
AF=CE
在Rt△ABF和Rt△CDE中,
AB=CD
AF=CE
∴
Rt△ABF≌Rt△CDE(HL)
∴
BF=DE
证明:∵BF⊥AC,DE⊥AC
∴∠BFA=∠DEC=90°
3、如图,AC、BD是正方形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有(
)
A.1个
B.2个
C.3个
D.4个
【解析】选D,在正方形ABCD中,△ADC、△ABD、△CBD都和△ABC全等,由题意不难得出四边形ACED为平行四边形,得出△DCE也和△ABC全等.
点拨运用(2分钟)
判定直角三角形全等的“两种思路”
1.若已知条件中有一组直角边和一组斜边分别相等,用“HL”判定.
2.不满足“斜边、直角边”,用其他4种判定。
课堂小结(2分钟)
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有特殊的判定方法:HL.
通过本课时的学习,需要我们掌握:
当堂训练(15分钟)
AD
=
BC
AC
=
BD
∠DAB=∠CBA
∠DBA
=
∠CAB
HL
HL
AAS
A
B
C
D
1.如图,AC⊥BC,BD⊥AD,要证△ABC≌△BAD,需要
添加一个什么条件?请说明理由.
(1)
(
);
(2)
(
);
(3)
(
);
(4)
(
).
2.如图,已知AB=CD,AE⊥BC,DF⊥BC,CE=BF。
部分共边
隐含条件:
D
A
B
C
F
E
AAS
求证:AE=DF。
2.如图,已知AB=CD,AE⊥BC,DF⊥BC,
CE=BF,求证:AE=DF。
D
A
B
C
F
E
选做题:
如图,已知:AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD,BE交于点O.
求证:AO平分∠BAC.
板书设计
直角三角形全等的条件
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”
).
几何语言:
∵ 在Rt△ABC
和
Rt△A'B'C'中,
AB
=A'B',
BC
=B'C',
∴ Rt△ABC
≌
Rt△A'B'C'(HL)
A
B
C
A'
B'
C'
1、判定两个三角形全等方法
,
,
,
。
SSS
ASA
AAS
SAS
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
以上的四种判别三角形全等的方法能不能用来判别Rt△全等呢?
C
B
A
12.2.4
三角形全等的判定
(HL)
学习目标(1分钟)
1、掌握判定直角三角形全等的一种
特殊方法——“斜边、直角边”
(即“HL”).
2、能熟练地用判定一般三角形全等的
方法及判定直角三角形全等的特殊
方法来判定两个直角三角形全等.
自学指导(5分钟)
1、如图,△ABC中,∠
C
=90°,直角边是_____、_____,斜边是______。
我们把直角△ABC记作Rt△ABC。
AC
BC
AB
∟
B
C
A
∟
C'?
2、再画一个Rt△A'B'C',使得∠C'=
90°,
B'C'=BC,A'B'=
AB。
A'?
B'?
把你所画的三角形与原三角形进行比较,看是否能重合?
归纳:斜边和一条直角边分别相等的两个直角三角形全等,简写为“斜边、直角边”或“HL”。
AB=A'B'
∵在Rt△ABC和Rt△A'B'C'中
Rt△ABC≌
Rt△A'B'C'
∴
(HL)
BC=B'C'
数
学
语
言
自学检测(9分钟)
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
在Rt△ACB和Rt△ADB中,
AB=AB,
AC=AD,
∴
Rt△ACB≌
Rt△ADB
(HL).
∴BC=BD
(全等三角形对应边相等).
解:∵∠C,∠D是直角
∴∠C=∠D=90°
A
F
C
E
D
B
2.如图,AB=CD,
BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE
∵
AE=CF
∴
AE+EF=CF+EF
即
AF=CE
在Rt△ABF和Rt△CDE中,
AB=CD
AF=CE
∴
Rt△ABF≌Rt△CDE(HL)
∴
BF=DE
证明:∵BF⊥AC,DE⊥AC
∴∠BFA=∠DEC=90°
3、如图,AC、BD是正方形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有(
)
A.1个
B.2个
C.3个
D.4个
【解析】选D,在正方形ABCD中,△ADC、△ABD、△CBD都和△ABC全等,由题意不难得出四边形ACED为平行四边形,得出△DCE也和△ABC全等.
点拨运用(2分钟)
判定直角三角形全等的“两种思路”
1.若已知条件中有一组直角边和一组斜边分别相等,用“HL”判定.
2.不满足“斜边、直角边”,用其他4种判定。
课堂小结(2分钟)
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有特殊的判定方法:HL.
通过本课时的学习,需要我们掌握:
当堂训练(15分钟)
AD
=
BC
AC
=
BD
∠DAB=∠CBA
∠DBA
=
∠CAB
HL
HL
AAS
A
B
C
D
1.如图,AC⊥BC,BD⊥AD,要证△ABC≌△BAD,需要
添加一个什么条件?请说明理由.
(1)
(
);
(2)
(
);
(3)
(
);
(4)
(
).
2.如图,已知AB=CD,AE⊥BC,DF⊥BC,CE=BF。
部分共边
隐含条件:
D
A
B
C
F
E
AAS
求证:AE=DF。
2.如图,已知AB=CD,AE⊥BC,DF⊥BC,
CE=BF,求证:AE=DF。
D
A
B
C
F
E
选做题:
如图,已知:AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD,BE交于点O.
求证:AO平分∠BAC.
板书设计
直角三角形全等的条件
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”
).
几何语言:
∵ 在Rt△ABC
和
Rt△A'B'C'中,
AB
=A'B',
BC
=B'C',
∴ Rt△ABC
≌
Rt△A'B'C'(HL)
A
B
C
A'
B'
C'
