北师大版九年级数学下学期第二章 二次函数章节巩固练(共16张ppt)
文档属性
| 名称 | 北师大版九年级数学下学期第二章 二次函数章节巩固练(共16张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 815.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 23:25:30 | ||
图片预览



文档简介
(共16张PPT)
你能从图案中找出多边形吗?
三条边相等三个角相等(60度)。
四条边相等四个角相等(900)
正三角形
正方形
什么样的图形是正多边形?
各边相等,各角也相等的多边形是正多边形.
矩形是正多边形吗?菱形呢?正方形呢?为什么?
你知道正多边形和圆有什么关系吗?怎样就能作出一个正多边形来?
正多边形都是轴对称图形,一个正n边形共有n
条对称轴,每条对称轴都通过n边形的中心。
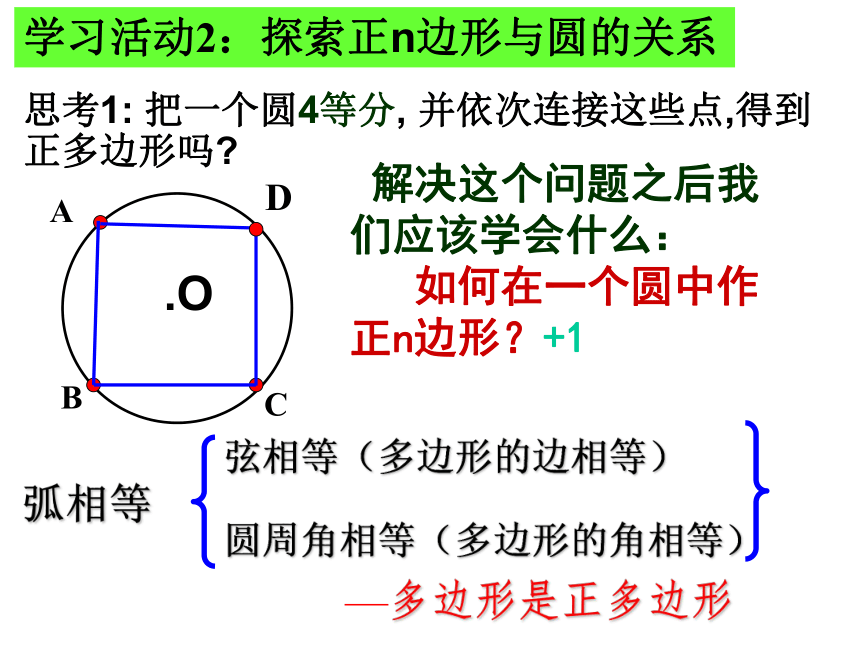
学习活动1:探索正多边形的对称性
边数是偶数的正多边形还是中心对称图形,
它的中心就是对称中心。
1.正n边形有几条对称轴?
每条对称轴都经过正n边形中的哪一个点?
2.正n边形是中心对称图形吗?
如果是,它的对称中心在哪里?
A
B
C
D
思考1:
把一个圆4等分,
并依次连接这些点,得到正多边形吗?
弧相等
弦相等(多边形的边相等)
圆周角相等(多边形的角相等)
—多边形是正多边形
学习活动2:探索正n边形与圆的关系
.O
解决这个问题之后我们应该学会什么:
如何在一个圆中作正n边形?+1
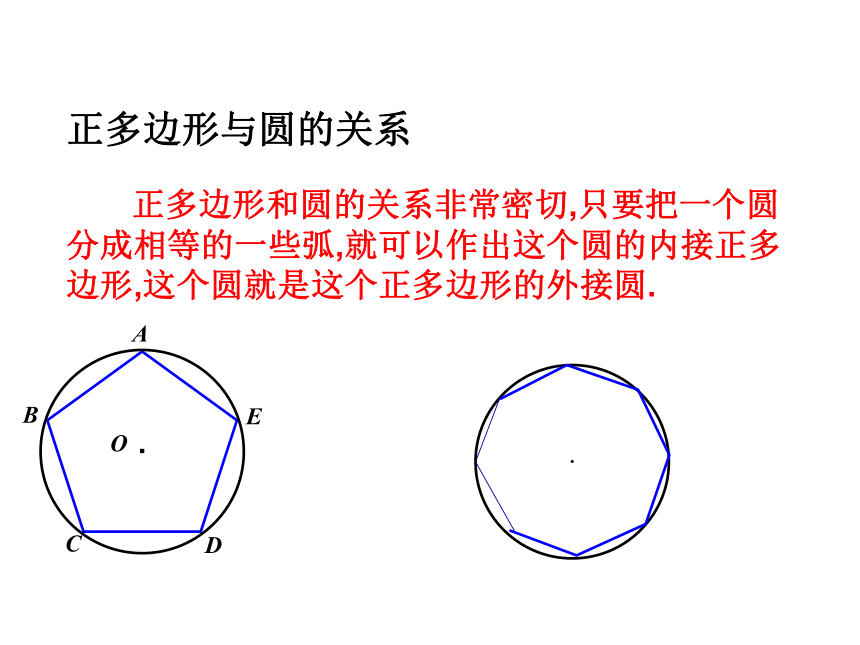
正多边形与圆的关系
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
·
A
B
C
D
E
O
·
学习活动3:了解正多边形有关的概念
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:
一个正多边形的
外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条
边所对的圆心角.
正多边形的边心距:
中心到正多边形的
一边的距离.
A
B
跟踪练习
1、O是正
的圆心,也是△ABC
的圆心。
△ABC的中心,它是△ABC
2、OB叫正△ABC的
它是正△ABC的
的半径。
3、OD叫作正△ABC的 它是正△ABC的
的半径。
A
B
C
.O
D
半径
外接圆
边心距
内切圆
外接圆
内切圆
1.作出下列正多边形的所有半径,请问正多边形被分成了几个什么样的三角形?+1
2.再作出每个正多边形的所有边心距,这时正多边形被分成了多少个什么样三角形?+1
正n边形的半径将正n边形分成n个全等的等腰三角形。边心距又把这n个等腰三角形分成了2n个全等的直角三角形.
学习活动4:探索正多边形的面积
我们该如何求正六边形的面积?
我们该如何求正n边形的面积?
(写出公式+1)
E
F
C
D
.
O
半径R
A
B
G
边心距d
边长为a
设正多边形的边长为a,半径为R,
边心距为d.它们三者之间有什么关系?+1
1.独立思考
2.小组交流
3.展示评价
例1、
有一个亭子它的地基是半径为4m的正六边形,
求地基的周长和面积。
F
A
D
E
.
.
O
B
C
r
R
P
1、有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).
解:
如图由于ABCDEF是正六边形,所以它的中心角等于
,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长
l
=4×6=24(m).
在Rt△OPC中,OC=4,
PC=
利用勾股定理,可得边心距
亭子地基的面积
O
A
B
C
D
E
F
R
P
r
1
、本节课你学到了哪些知识?
2、对于本节课所学知识你还有哪些困惑?
如图,正三角形ABC的边心距
r
=2,求:R,
a
,
A
B
C
O
D
S
你能从图案中找出多边形吗?
三条边相等三个角相等(60度)。
四条边相等四个角相等(900)
正三角形
正方形
什么样的图形是正多边形?
各边相等,各角也相等的多边形是正多边形.
矩形是正多边形吗?菱形呢?正方形呢?为什么?
你知道正多边形和圆有什么关系吗?怎样就能作出一个正多边形来?
正多边形都是轴对称图形,一个正n边形共有n
条对称轴,每条对称轴都通过n边形的中心。
学习活动1:探索正多边形的对称性
边数是偶数的正多边形还是中心对称图形,
它的中心就是对称中心。
1.正n边形有几条对称轴?
每条对称轴都经过正n边形中的哪一个点?
2.正n边形是中心对称图形吗?
如果是,它的对称中心在哪里?
A
B
C
D
思考1:
把一个圆4等分,
并依次连接这些点,得到正多边形吗?
弧相等
弦相等(多边形的边相等)
圆周角相等(多边形的角相等)
—多边形是正多边形
学习活动2:探索正n边形与圆的关系
.O
解决这个问题之后我们应该学会什么:
如何在一个圆中作正n边形?+1
正多边形与圆的关系
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
·
A
B
C
D
E
O
·
学习活动3:了解正多边形有关的概念
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:
一个正多边形的
外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条
边所对的圆心角.
正多边形的边心距:
中心到正多边形的
一边的距离.
A
B
跟踪练习
1、O是正
的圆心,也是△ABC
的圆心。
△ABC的中心,它是△ABC
2、OB叫正△ABC的
它是正△ABC的
的半径。
3、OD叫作正△ABC的 它是正△ABC的
的半径。
A
B
C
.O
D
半径
外接圆
边心距
内切圆
外接圆
内切圆
1.作出下列正多边形的所有半径,请问正多边形被分成了几个什么样的三角形?+1
2.再作出每个正多边形的所有边心距,这时正多边形被分成了多少个什么样三角形?+1
正n边形的半径将正n边形分成n个全等的等腰三角形。边心距又把这n个等腰三角形分成了2n个全等的直角三角形.
学习活动4:探索正多边形的面积
我们该如何求正六边形的面积?
我们该如何求正n边形的面积?
(写出公式+1)
E
F
C
D
.
O
半径R
A
B
G
边心距d
边长为a
设正多边形的边长为a,半径为R,
边心距为d.它们三者之间有什么关系?+1
1.独立思考
2.小组交流
3.展示评价
例1、
有一个亭子它的地基是半径为4m的正六边形,
求地基的周长和面积。
F
A
D
E
.
.
O
B
C
r
R
P
1、有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).
解:
如图由于ABCDEF是正六边形,所以它的中心角等于
,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长
l
=4×6=24(m).
在Rt△OPC中,OC=4,
PC=
利用勾股定理,可得边心距
亭子地基的面积
O
A
B
C
D
E
F
R
P
r
1
、本节课你学到了哪些知识?
2、对于本节课所学知识你还有哪些困惑?
如图,正三角形ABC的边心距
r
=2,求:R,
a
,
A
B
C
O
D
S
同课章节目录
