锐角三角函数
图片预览






文档简介
(共71张PPT)
怎样求出小山的高度
新课导入
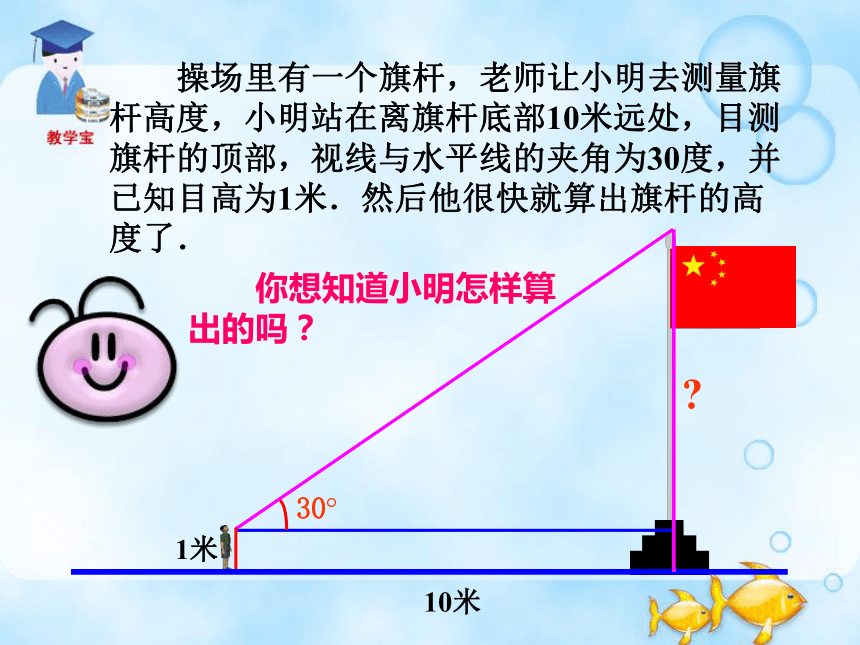
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1米.然后他很快就算出旗杆的高度了.
1米
10米
你想知道小明怎样算出的吗?
【知识与技能】
1.了解三角函数的概念,理解正弦、余弦、正切的概念; 2. 掌握在直角三角形之中,锐角三角函数与两边之比的对应关系; 3.掌握锐角三角函数的概念并会求一个锐角的三角函数值.
教学目标
【过程与方法】 1.通过经历三角函数概念的形成过程,丰富自己的数学活动经验;
2.渗透数形结合的数学思想方法.
【情感态度与价值观】
1.感受数学来源于生活又应用于生活,体验数学的生活化经历; 2.培养主动探索,敢于实践,勇于发现,合作交流的精神.
重点:
锐角三角函数的概念.
难点:
锐角三角函数概念的形成.
教学重难点
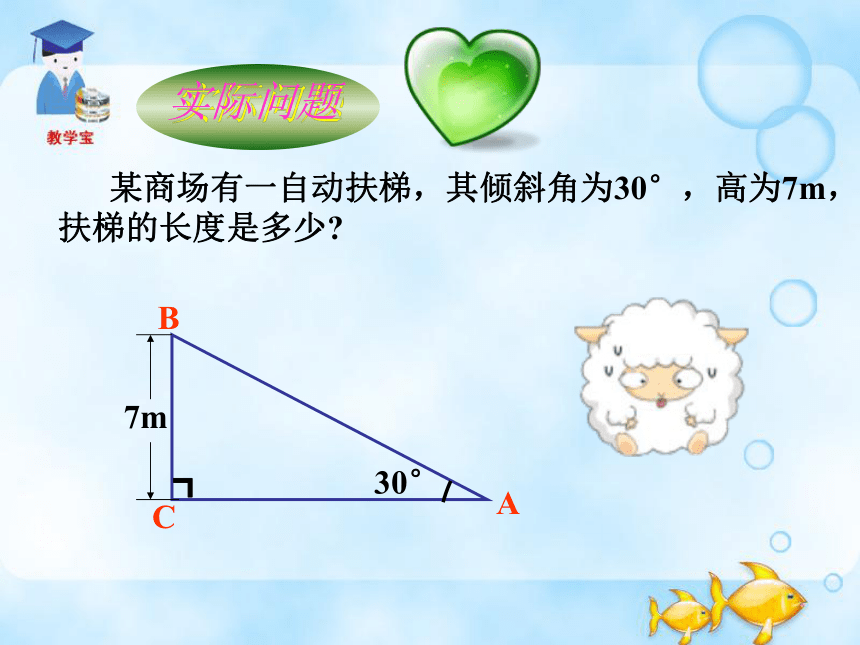
某商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少
B
A
C
┓
30°
7m
实际问题
解:这个问题可以归结为,在Rt△ABC中,∠C=90 °,∠A=30 °,BC=7m,求AB.
∵在直角三角形中, 由于∠A=30 °,
所以
可得AB=2BC=7×2=14m
所以,扶梯的长度是14m.
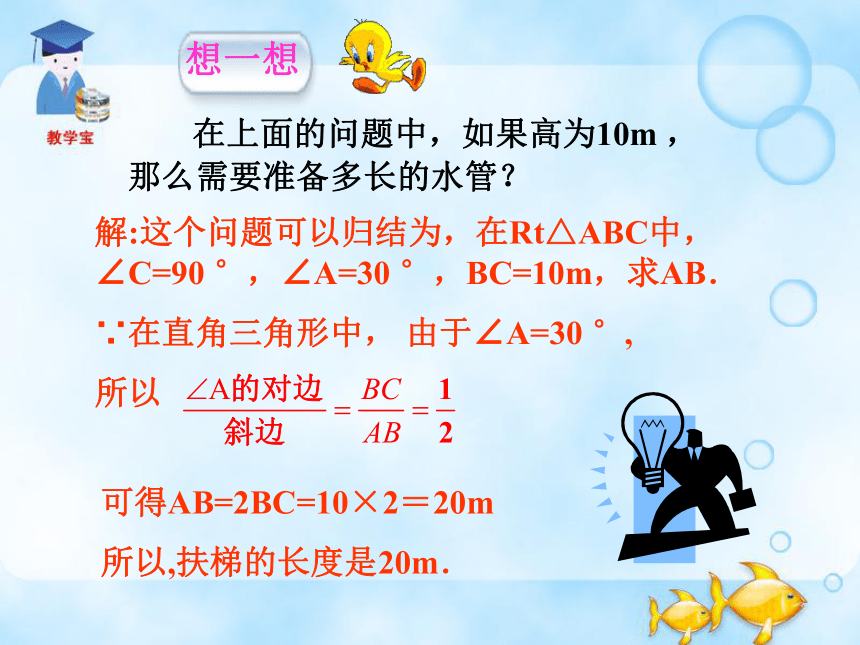
在上面的问题中,如果高为10m ,那么需要准备多长的水管?
解:这个问题可以归结为,在Rt△ABC中,∠C=90 °,∠A=30 °,BC=10m,求AB.
∵在直角三角形中, 由于∠A=30 °,
所以
想一想
可得AB=2BC=10×2=20m
所以,扶梯的长度是20m.
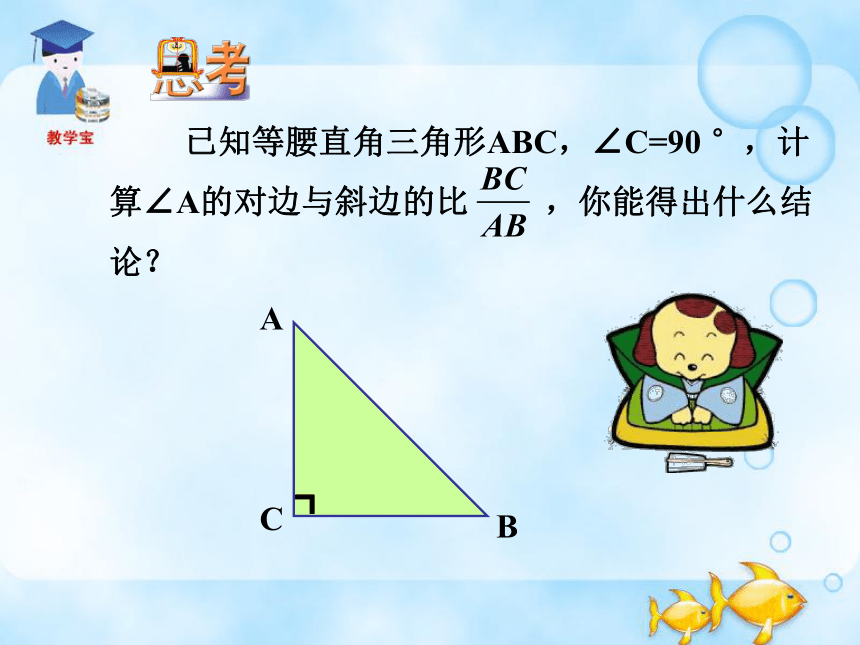
已知等腰直角三角形ABC,∠C=90 °,计算∠A的对边与斜边的比 ,你能得出什么结论?
A
B
C
┓
解:因为△ABC是等腰直角三角形, ∠C=90 °,所以∠A=45 °.
由勾股定理得
A
B
C
┓
即直角三角形中,当一个角等于45°时,这个角的对边与斜边的比都等于 .
因此
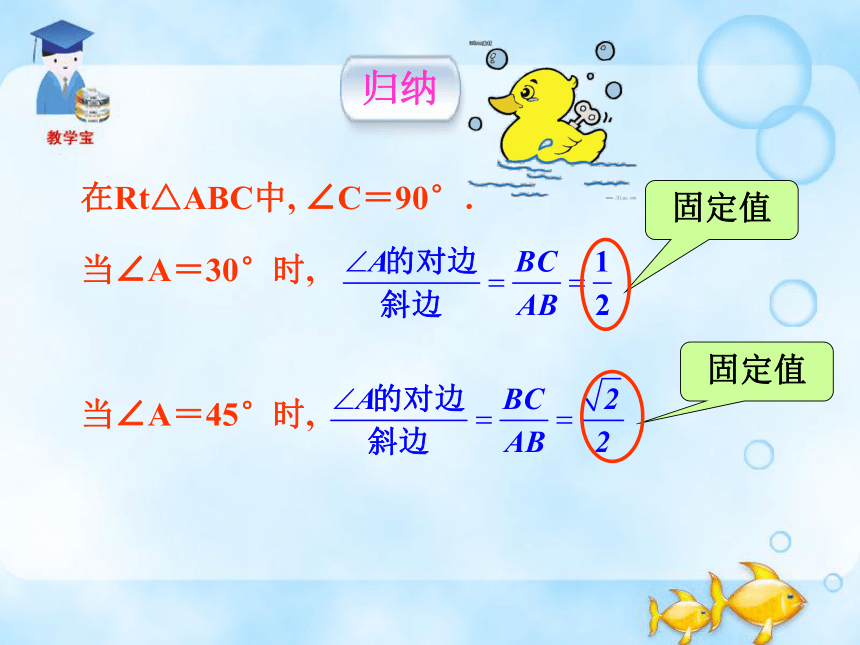
在Rt△ABC中, ∠C=90°.
当∠A=30°时,
当∠A=45°时,
固定值
固定值
归纳
对于锐角A的每一个确定的值,其对边与斜边的比值也是惟一确定的 吗?
想一想
所以 =__________=__________.
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以,在Rt△ABC中,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何, ∠A的对边与斜边的比是一个固定值.
观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,∠A的对边与斜边有什么关系?
直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
┓
C
A
B
斜边
c
邻边
对边
a
b
C
A
B
┓
C
A
B
在Rt△ABC中, ∠C=90 °,我们把锐角A的对边与斜边的比叫做∠ A的正弦(sine),记作sinA,即
一个角的正弦表示定值、比值、正值.
知识要点
正弦
【例1】如图,在Rt△ABC中, ∠C=90 °,求sinA和sinB的值.
A
B
C
A
B
C
┓
┓
6
8
(1)
(2)
A
B
C
┓
6
8
(1)
解:设如图所示,在Rt△ABC中,
因此
A
B
C
┓
(2)
解:设如图所示,在Rt△ABC中,
因此
如图,求sinA和sinB的值.
A
B
C
A
B
C
┓
┓
10
(1)
(2)
26
9
40
小练习
对于锐角A的每一个确定的值,其邻边与斜边、邻边与对边的比值也是惟一确定的吗?
想一想
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =__________=__________.
观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,∠A的邻边与斜边、 ∠A的对边与邻边之间有什么关系?
=__________=__________.
在Rt△ABC中,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何, ∠A的∠A的邻边与斜边的比、 ∠A的对边与邻边的比都是一个固定值.
在Rt△ABC中,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,
∠A的对边边与斜边的比、
∠A的邻边与斜边的比、
∠A的对边与邻边的比都是一个固定值.
归纳
在Rt△ABC中, ∠C=90 °,我们把锐角A的邻边与斜边的比叫做∠ A的余弦(cosine),记作cosA,即
一个角的余弦表示定值、比值、正值.
知识要点
余弦
在Rt△ABC中, ∠C=90 °,我们把锐角A的对边与邻边的比叫做∠ A的正切(tangent),记作tanA,即
一个角的余切表示定值、比值、正值.
知识要点
正切
在Rt△ABC中, ∠C=90 °,我们把锐角A的邻边与对边的比叫做∠ A的余切,记作cotA,即
一个角的余切表示定值、比值、正值.
知识要点
余切
tan30°=
A
B
C
┌
锐角A的正切值可以等于1吗?为什么?
可以大于1吗?
tan 45°=
tan 60°=
锐角三角函数
锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数(trigonometric function of acute angle)
知识要点
1.sinA、cosA、tanA 、 cotA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA、 cosA、tanA 、 cotA是一个比值(数值).
3.sinA、 cosA、 tanA 、 cotA的大小只与∠A的大小有关,而与直角三角形的边长无关.
归纳
【例2】如图,在Rt△ABC中, ∠C=90 °,BC=24,sinA= ,求cosA、tanB的值.
A
B
C
┓
24
解:∵
∴
又
∴
A
B
C
┓
24
分别求出下列直角三角形中的锐角的正弦值、余弦值和正切值、余切值.
A
B
C
┓
(1)
A
B
C
┓
5
(2)
25
7
小练习
如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
抢答
如图,观察一副三角板:它们其中有几个锐角 分别是多少度 分别求出这几个锐角的三角函数.
A
B
C
30°
1
2
sin30°=
cos30°=
tan30°=
cot30°=
┓
A
B
C
45°
1
1
sin45 ° =
cos45°=
tan45°=
cot45°=
1
1
┓
A
C
B
60°
1
2
sin60°=
cos60°=
tan60°=
cot60°=
┓
30 ° 45 ° 60 °
sinα
cosα
tanα
cotα
特殊角的三角函数值表
自变量α的取值范围是:
各因变量的取值范围是:
0°<α< 90°
正弦 0< sinα<1
余弦 0< cosα<1
正切 tanα>0
余切 cotα>0
根据上面表格,思考以下问题:
各个函数值随着自变量α的增大而怎样变化?tanα与cotα有怎样的关系?
sinα、tanα随着自变量α的增大而增大 cosα、cotα随着自变量α的增大而减小
tanα cotα =1
当两角互余时,这两角的正弦和余弦有怎样的关系?正切和余切呢?
sinα= cos(90°-α)
cosα= sin(90°-α)
tanα= cot(90°-α)
cotα= tan(90°-α)
sin2α+cos2α=1
【例3】求下列各式的值:
解:
(1)sin60°+cos45°;
(2) sin230°+cos245°+tan60°.
解: (1)sin30°+cos45°
(2) sin260°+cos260°-cot45°
小练习
如果知道一个角的三角函数的数值,你能求出这个角是多少度吗?
(1)已知 ,则∠A=________;
(2)已知 ,则∠B=________;
(3)已知 ,则∠C=________;
(4)已知 ,则∠D=________;
30°
60°
60°
30°
探究
由锐角的三角函数值反求锐角
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
归纳
【例4】 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
∴最高位置与最低位置的高度差约为0.34m.
∠AOD OD=2.5m,
解:如图,根据题意可知,
∴AC=2.5-2.165≈0.34(m).
如图,在Rt△ABC中,∠C=90°,∠A,∠B ,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1.
证明:
小练习
b
A
B
C
a
c
┏
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=17°,那么缆车垂直上升的距离是多少
解:在Rt△ABC中,∠C=90°,
BC=ABsin17° .
你知道sin17°等于多少吗
用科学计算器求锐角的三角函数值:
sin
cos
tan
用计算器求sin18°,cos53°, tan72°, cot65°和sin72° 38′25″的三角函数.
按键的顺序 显示结果
sin18°
cos53°
tan72°
cot62°
sin72° 38′25″
sin
1
8
°′″
0.309 016 994
cos
5
3
°′″
0.601 815 023
tan
7
2
°′″
3.732 050 808
sin
7
2
°′″
3
8
°′″
2
5
°′″
0.954 450 312
=
=
=
=
cot
6
2
°′″
=
0.531 709 432
用计算器求三角函数值时,结果一般有10个数位.本书约定,如无特别声明,计算结果一般精确到万分位.
所以我们可以用计算器求得缆车上升的垂直距离: BC=ABsin17°≈200×0.2924≈58.48(m).
如图,为了方便行人,市政府在10m高的天桥.两端修建了40m长的斜道.这条斜道的倾斜角是多少
如图,在Rt△ABC中,
∠A是多少度
A
B
C
40m
10m
如图,一名患者体内某重要器官后面有一肿瘤.在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必需从侧面照射肿瘤.已知肿瘤在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求射线的入射角度.
解:如图,在Rt△ABC中,AC=6.3cm,BC=9.8cm.
∴∠B≈32°44′13″.
因此,射线的入射角度约为32°44′13″.
小练习
已知三角函数值求角度,要用到三个键, 和第二功能键 和 .
sin
cos
tan
按键的顺序 显示结果
sinA=0.9816
cosA=0.8607
tanA=0.1890
tanA=56.78
shift
sin-1
0
.
sin-1=0.9816
=78.99184039
shift
cos-1
0
.
cos-1=0.8607
=30.60473007
shift
tan-1
0
.
tan-1=0.1890
=10.70265749
shift
tan-1
5
6
.
7
8
tan-1=56.78
=88.99102049
9
8
1
=
sin-1
cos-1
tan-1
shift
8
1
6
=
6
0
7
=
8
9
0
=
上表的显示结果是以度为单位的,再按 键即可显示以“度,分,秒”为单位的结果.
dms
根据下列条件计算器求∠θ的大小:
(1)tanθ=2.9888;
(2)sinθ=0.3957;
(3)cosθ=0.7850;
(4)tanθ=0.8972.
小练习
71.5°
23.3°
38.3°
41.9°
1.锐角∠A的正弦、余弦、正切、余切函数,统称为 锐角∠A的三角函数.
2.30°、45°、60°角的三角函数值.
3.锐角α的三角函数值的取值范围 .
4.三角函数的增减性:
正弦 0< sinα<1 正切 tanα>0
余弦 0< cosα<1 余切 cotα>0
sinα、tanα随着自变量α的增大而增大
cosα、cotα随着自变量α的增大而减小
课堂小结
tanα cot(90°-α) =1
sin2 α +cos2 (90°-α) =1
sinα= cos(90°-α)
cosα= sin(90°-α)
tanα= cot(90°-α)
cotα = tan(90°-α)
5.三角函数的几个重要关系式
1.当∠A为锐角,且tanA的值大于
时,∠A( )
A.小于30° B.大于30°
C.小于60° D.大于60°
D
随堂练习
2.当∠A为锐角,且cotA的值小于 时,
∠A( )
A.小于30° B.大于30°
C.小于60° D.大于60°
D
当∠A为锐角,且cosA= 那么( )
A.0°<∠A≤ 30 ° B .30°<∠A≤45°
C.45°<∠A≤ 60 ° D.60°<∠A≤ 90 °
D
4.当锐角A>45°时,sinA的值( )
A.小于 B.大于
C.小于 D.大于
B
A.小于 B.大于
C.小于 D.大于
5.当锐角A>30°时,cotA的值( )
C
6.计算:
(1) 2sin30°+3cos30°+cot45°
(2) cos230°+ tan60°sin30°
0
∴ 3cosA =
7.已知3tanA — = 0 ,求锐角A的度数 .
解:3tanA- = 0
∴cosA=
∴∠A= 60°
8.求出如图所示的Rt△ABC中∠A的四个三角函数值.
解:∵
∴ sinA =
cosA =
tanA =
cotA =
17
15
8
C
B
A
9.如图,在直角坐标平面中,P是第一象限的点,其坐标是(3,y),且OP与x轴的正半轴的夹角a的正切值是 ,求:
(1) y的值; (2) ∠a的正弦值.
(1)y =4
(2)sina=
●
O
x
y
P(3,y)
α
(1)sinA= ,cosA= ,
tanA= ,sinB= ,
cosA= ,tanB= ,
2. 确定.因为一个锐角确定的直角三角形都相似.
习题答案
怎样求出小山的高度
新课导入
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1米.然后他很快就算出旗杆的高度了.
1米
10米
你想知道小明怎样算出的吗?
【知识与技能】
1.了解三角函数的概念,理解正弦、余弦、正切的概念; 2. 掌握在直角三角形之中,锐角三角函数与两边之比的对应关系; 3.掌握锐角三角函数的概念并会求一个锐角的三角函数值.
教学目标
【过程与方法】 1.通过经历三角函数概念的形成过程,丰富自己的数学活动经验;
2.渗透数形结合的数学思想方法.
【情感态度与价值观】
1.感受数学来源于生活又应用于生活,体验数学的生活化经历; 2.培养主动探索,敢于实践,勇于发现,合作交流的精神.
重点:
锐角三角函数的概念.
难点:
锐角三角函数概念的形成.
教学重难点
某商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少
B
A
C
┓
30°
7m
实际问题
解:这个问题可以归结为,在Rt△ABC中,∠C=90 °,∠A=30 °,BC=7m,求AB.
∵在直角三角形中, 由于∠A=30 °,
所以
可得AB=2BC=7×2=14m
所以,扶梯的长度是14m.
在上面的问题中,如果高为10m ,那么需要准备多长的水管?
解:这个问题可以归结为,在Rt△ABC中,∠C=90 °,∠A=30 °,BC=10m,求AB.
∵在直角三角形中, 由于∠A=30 °,
所以
想一想
可得AB=2BC=10×2=20m
所以,扶梯的长度是20m.
已知等腰直角三角形ABC,∠C=90 °,计算∠A的对边与斜边的比 ,你能得出什么结论?
A
B
C
┓
解:因为△ABC是等腰直角三角形, ∠C=90 °,所以∠A=45 °.
由勾股定理得
A
B
C
┓
即直角三角形中,当一个角等于45°时,这个角的对边与斜边的比都等于 .
因此
在Rt△ABC中, ∠C=90°.
当∠A=30°时,
当∠A=45°时,
固定值
固定值
归纳
对于锐角A的每一个确定的值,其对边与斜边的比值也是惟一确定的 吗?
想一想
所以 =__________=__________.
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以,在Rt△ABC中,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何, ∠A的对边与斜边的比是一个固定值.
观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,∠A的对边与斜边有什么关系?
直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
┓
C
A
B
斜边
c
邻边
对边
a
b
C
A
B
┓
C
A
B
在Rt△ABC中, ∠C=90 °,我们把锐角A的对边与斜边的比叫做∠ A的正弦(sine),记作sinA,即
一个角的正弦表示定值、比值、正值.
知识要点
正弦
【例1】如图,在Rt△ABC中, ∠C=90 °,求sinA和sinB的值.
A
B
C
A
B
C
┓
┓
6
8
(1)
(2)
A
B
C
┓
6
8
(1)
解:设如图所示,在Rt△ABC中,
因此
A
B
C
┓
(2)
解:设如图所示,在Rt△ABC中,
因此
如图,求sinA和sinB的值.
A
B
C
A
B
C
┓
┓
10
(1)
(2)
26
9
40
小练习
对于锐角A的每一个确定的值,其邻边与斜边、邻边与对边的比值也是惟一确定的吗?
想一想
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =__________=__________.
观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,∠A的邻边与斜边、 ∠A的对边与邻边之间有什么关系?
=__________=__________.
在Rt△ABC中,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何, ∠A的∠A的邻边与斜边的比、 ∠A的对边与邻边的比都是一个固定值.
在Rt△ABC中,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,
∠A的对边边与斜边的比、
∠A的邻边与斜边的比、
∠A的对边与邻边的比都是一个固定值.
归纳
在Rt△ABC中, ∠C=90 °,我们把锐角A的邻边与斜边的比叫做∠ A的余弦(cosine),记作cosA,即
一个角的余弦表示定值、比值、正值.
知识要点
余弦
在Rt△ABC中, ∠C=90 °,我们把锐角A的对边与邻边的比叫做∠ A的正切(tangent),记作tanA,即
一个角的余切表示定值、比值、正值.
知识要点
正切
在Rt△ABC中, ∠C=90 °,我们把锐角A的邻边与对边的比叫做∠ A的余切,记作cotA,即
一个角的余切表示定值、比值、正值.
知识要点
余切
tan30°=
A
B
C
┌
锐角A的正切值可以等于1吗?为什么?
可以大于1吗?
tan 45°=
tan 60°=
锐角三角函数
锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数(trigonometric function of acute angle)
知识要点
1.sinA、cosA、tanA 、 cotA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA、 cosA、tanA 、 cotA是一个比值(数值).
3.sinA、 cosA、 tanA 、 cotA的大小只与∠A的大小有关,而与直角三角形的边长无关.
归纳
【例2】如图,在Rt△ABC中, ∠C=90 °,BC=24,sinA= ,求cosA、tanB的值.
A
B
C
┓
24
解:∵
∴
又
∴
A
B
C
┓
24
分别求出下列直角三角形中的锐角的正弦值、余弦值和正切值、余切值.
A
B
C
┓
(1)
A
B
C
┓
5
(2)
25
7
小练习
如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
抢答
如图,观察一副三角板:它们其中有几个锐角 分别是多少度 分别求出这几个锐角的三角函数.
A
B
C
30°
1
2
sin30°=
cos30°=
tan30°=
cot30°=
┓
A
B
C
45°
1
1
sin45 ° =
cos45°=
tan45°=
cot45°=
1
1
┓
A
C
B
60°
1
2
sin60°=
cos60°=
tan60°=
cot60°=
┓
30 ° 45 ° 60 °
sinα
cosα
tanα
cotα
特殊角的三角函数值表
自变量α的取值范围是:
各因变量的取值范围是:
0°<α< 90°
正弦 0< sinα<1
余弦 0< cosα<1
正切 tanα>0
余切 cotα>0
根据上面表格,思考以下问题:
各个函数值随着自变量α的增大而怎样变化?tanα与cotα有怎样的关系?
sinα、tanα随着自变量α的增大而增大 cosα、cotα随着自变量α的增大而减小
tanα cotα =1
当两角互余时,这两角的正弦和余弦有怎样的关系?正切和余切呢?
sinα= cos(90°-α)
cosα= sin(90°-α)
tanα= cot(90°-α)
cotα= tan(90°-α)
sin2α+cos2α=1
【例3】求下列各式的值:
解:
(1)sin60°+cos45°;
(2) sin230°+cos245°+tan60°.
解: (1)sin30°+cos45°
(2) sin260°+cos260°-cot45°
小练习
如果知道一个角的三角函数的数值,你能求出这个角是多少度吗?
(1)已知 ,则∠A=________;
(2)已知 ,则∠B=________;
(3)已知 ,则∠C=________;
(4)已知 ,则∠D=________;
30°
60°
60°
30°
探究
由锐角的三角函数值反求锐角
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
归纳
【例4】 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
∴最高位置与最低位置的高度差约为0.34m.
∠AOD OD=2.5m,
解:如图,根据题意可知,
∴AC=2.5-2.165≈0.34(m).
如图,在Rt△ABC中,∠C=90°,∠A,∠B ,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1.
证明:
小练习
b
A
B
C
a
c
┏
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=17°,那么缆车垂直上升的距离是多少
解:在Rt△ABC中,∠C=90°,
BC=ABsin17° .
你知道sin17°等于多少吗
用科学计算器求锐角的三角函数值:
sin
cos
tan
用计算器求sin18°,cos53°, tan72°, cot65°和sin72° 38′25″的三角函数.
按键的顺序 显示结果
sin18°
cos53°
tan72°
cot62°
sin72° 38′25″
sin
1
8
°′″
0.309 016 994
cos
5
3
°′″
0.601 815 023
tan
7
2
°′″
3.732 050 808
sin
7
2
°′″
3
8
°′″
2
5
°′″
0.954 450 312
=
=
=
=
cot
6
2
°′″
=
0.531 709 432
用计算器求三角函数值时,结果一般有10个数位.本书约定,如无特别声明,计算结果一般精确到万分位.
所以我们可以用计算器求得缆车上升的垂直距离: BC=ABsin17°≈200×0.2924≈58.48(m).
如图,为了方便行人,市政府在10m高的天桥.两端修建了40m长的斜道.这条斜道的倾斜角是多少
如图,在Rt△ABC中,
∠A是多少度
A
B
C
40m
10m
如图,一名患者体内某重要器官后面有一肿瘤.在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必需从侧面照射肿瘤.已知肿瘤在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求射线的入射角度.
解:如图,在Rt△ABC中,AC=6.3cm,BC=9.8cm.
∴∠B≈32°44′13″.
因此,射线的入射角度约为32°44′13″.
小练习
已知三角函数值求角度,要用到三个键, 和第二功能键 和 .
sin
cos
tan
按键的顺序 显示结果
sinA=0.9816
cosA=0.8607
tanA=0.1890
tanA=56.78
shift
sin-1
0
.
sin-1=0.9816
=78.99184039
shift
cos-1
0
.
cos-1=0.8607
=30.60473007
shift
tan-1
0
.
tan-1=0.1890
=10.70265749
shift
tan-1
5
6
.
7
8
tan-1=56.78
=88.99102049
9
8
1
=
sin-1
cos-1
tan-1
shift
8
1
6
=
6
0
7
=
8
9
0
=
上表的显示结果是以度为单位的,再按 键即可显示以“度,分,秒”为单位的结果.
dms
根据下列条件计算器求∠θ的大小:
(1)tanθ=2.9888;
(2)sinθ=0.3957;
(3)cosθ=0.7850;
(4)tanθ=0.8972.
小练习
71.5°
23.3°
38.3°
41.9°
1.锐角∠A的正弦、余弦、正切、余切函数,统称为 锐角∠A的三角函数.
2.30°、45°、60°角的三角函数值.
3.锐角α的三角函数值的取值范围 .
4.三角函数的增减性:
正弦 0< sinα<1 正切 tanα>0
余弦 0< cosα<1 余切 cotα>0
sinα、tanα随着自变量α的增大而增大
cosα、cotα随着自变量α的增大而减小
课堂小结
tanα cot(90°-α) =1
sin2 α +cos2 (90°-α) =1
sinα= cos(90°-α)
cosα= sin(90°-α)
tanα= cot(90°-α)
cotα = tan(90°-α)
5.三角函数的几个重要关系式
1.当∠A为锐角,且tanA的值大于
时,∠A( )
A.小于30° B.大于30°
C.小于60° D.大于60°
D
随堂练习
2.当∠A为锐角,且cotA的值小于 时,
∠A( )
A.小于30° B.大于30°
C.小于60° D.大于60°
D
当∠A为锐角,且cosA= 那么( )
A.0°<∠A≤ 30 ° B .30°<∠A≤45°
C.45°<∠A≤ 60 ° D.60°<∠A≤ 90 °
D
4.当锐角A>45°时,sinA的值( )
A.小于 B.大于
C.小于 D.大于
B
A.小于 B.大于
C.小于 D.大于
5.当锐角A>30°时,cotA的值( )
C
6.计算:
(1) 2sin30°+3cos30°+cot45°
(2) cos230°+ tan60°sin30°
0
∴ 3cosA =
7.已知3tanA — = 0 ,求锐角A的度数 .
解:3tanA- = 0
∴cosA=
∴∠A= 60°
8.求出如图所示的Rt△ABC中∠A的四个三角函数值.
解:∵
∴ sinA =
cosA =
tanA =
cotA =
17
15
8
C
B
A
9.如图,在直角坐标平面中,P是第一象限的点,其坐标是(3,y),且OP与x轴的正半轴的夹角a的正切值是 ,求:
(1) y的值; (2) ∠a的正弦值.
(1)y =4
(2)sina=
●
O
x
y
P(3,y)
α
(1)sinA= ,cosA= ,
tanA= ,sinB= ,
cosA= ,tanB= ,
2. 确定.因为一个锐角确定的直角三角形都相似.
习题答案
