2020年人教版八年级上册数学期中复习(基础)学案(无答案)
文档属性
| 名称 | 2020年人教版八年级上册数学期中复习(基础)学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 304.1KB | ||
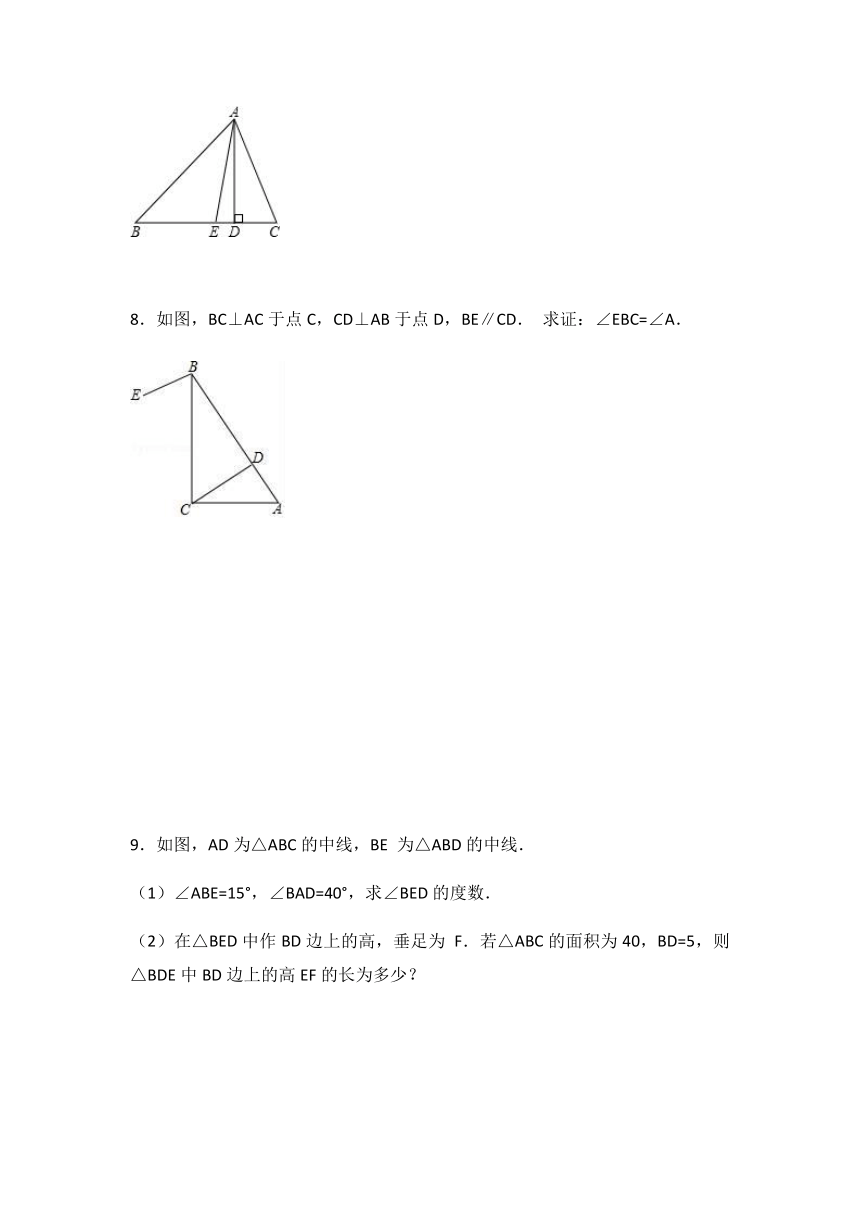
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览




文档简介
知识梳理+例题
知识点1:三角形的三边
(1)知识点:
三角形任意两边之和大于第三边:b+c>a
三角形任意两边之差小于第三边:b-c(2)例题:
以下列数据为长度的三条线段,能组成三角形的是:(
)
A.2cm、3cm、5cm
B.2cm、3cm、4cm
C.3cm、5cm、9cm
D.8cm、4cm、4cm
2.小芳有两根长度为4cm和9cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A.3cm
B.5cm
C.12cm
D.17cm
3.一个等腰三角形的两边长分别是3和7,则它的周长为( )
A.13
B.15
C.17
D.13或17
知识点2:三角形的内角和及外角
(1)知识点:
三角形三个内角的和是180°
在直角三角形中,两个锐角互余.
三角形的一个外角等于与它不相邻的两个内角的和.
(2)例题:
1.在△ABC中,∠A:∠B:∠C=2:3:4,则∠C=____________.
2.如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是 .
3.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85°
B.80°
C.75°
D.70°
4.∠ACD是△ABC的外角,∠ACD=80°,∠B=30°,则∠A的度数为 .
5.如图,把一根直尺与一块三角尺如图放置,若么∠1=55?,则∠2的度数为___.
6.如图,在△ABC中,∠B=46?,∠C=54?,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,求∠ADE的大小。
7.如图,在△ABC中,AE是∠BAC的角平分线,AD是BC边上的高,且∠B=40°,∠C=60°,求∠EAD的度数.
8.如图,BC⊥AC于点C,CD⊥AB于点D,BE∥CD.
求证:∠EBC=∠A.
9.如图,AD为△ABC的中线,BE
为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数.
(2)在△BED中作BD边上的高,垂足为
F.若△ABC的面积为40,BD=5,则△BDE中BD边上的高EF的长为多少?
10.小明在学习过程中,对教材中的一个有趣问题做如下探究:
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
知识点3:多边形的内角和、外角和及对角线数
(1)知识点:
从n边形一个顶点可以引(n-3)条对角线,将多边形分成(n-2)个三角形。
n边形共有条对角线。
n边形的内角和等于(n-2)·180°(n≥3,n是正整数)。任意凸形多边形的外角和等于360°
(2)例题:
1.若一个多边形的内角和和外角和相加是2160°,则次多边形是(
)
A.八边形
B.十边形
C.十二边形
D.十四边形
2.一个正多边形的每个外角都等于36°,那么它是( )
A.正五边形
B.正六边形
C.正八边形
D.正十边形
3.已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )
A.6
B.7
C.8
D.9
4.一个多边形的内角和是它的外角和的4倍,这个多边形是__________边形.
知识点4:全等三角形的性质
(1)知识点:
全等的图形必须满足:(1)形状相同的图形;(2)大小相等的图形;
全等三角形的性质
(1)全等三角形对应边相等;
(2)全等三角形对应角相等;
(2)例题:
1.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
2.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2
B.3
C.5
D.2.5
知识点5:全等三角形的证明
(1)知识点:
(1)三边对应相等的两个三角形全等。(SSS)
(2)两角和它们的夹边对应相等的两个三角形全等。(ASA)
(3)两角和其中一角的对边对应相等的两个三角形全等。(AAS)
(4)两边和它们的夹角对应相等的两个三角形全等。(SAS)
(5)斜边和一条直角边对应相等的两个直角三角形全等。(HL)
(2)例题:
1.下列条件不可以判定两个直角三角形全等的是()
两条直角边对应相等
B.一条直角边和它所对的锐角对应相等
C.两个锐角对应相等
D.一个锐角和锐角所对的直角边对应相等
2.如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD,你添加的条件是
.
3.如图,已知
AB⊥BD,ED⊥BD,AB=ED,要说明△ABC≌△EDC,
①若以“SAS”为判定依据,还要添加的一个条件为 ;
②若添加条件AC=EC,则可以依据 判定全等.
4、如图,AF=CE,AD∥CB,∠B=∠D,
(1)求证:△ADF≌△CBE.
(2)若∠D=20°,∠C=25°,求∠AEB的度数.
5.已知:如图,A,E,B,D在同一直线上,AE=DB,∠A=∠D,BC∥EF.求证:△ABC≌△DEF.
6、在等边△ABC中,点D是线段BC的中点,∠EDF=120?,线段DE与线段AB相交于点E.
线段DF与线段AC相交于点F.
如图,若DF⊥AC,求∠AED的度数.
求证:DE=DF.
7.如图,在一个风筝ABCD中,AB=AD,BC=DC,分别在AB、AD的中点E、F处贴两根彩线EC、FC.
(1)∠B
与∠D相等吗?请说明理由;
(2)求证:EC=FC.
8.如图1,在线段BE上取一点C,分别以CB,CE为腰作等腰直角△BCA和等腰直角△DCE,连接BD和AE.
(1)请判断线段BD和线段AE的数量关系,并说明理由;
9、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B.
C.?E在同一条直线上,连结DC.
(1)请在图2中找出与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
10、如图,已知在△ABC中,AB=AC=10cm,BC=9cm,D为AB中点,设点P在线段BC上以3cm/s的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.
(1)若Q点运动的速度与P点相同,且点P、Q同时出发,经过1秒钟后△BPD与△CQP是否全等,并说明理由;
知识点6:角平分线的性质
(1)知识点:
①角的平分线上的点到角的两边的距离相等.
PD
=
PE.
应满足的条件:
(1)角的平分线;(2)点在角平分线上;(3)垂直距离.
②角的内部到角的两边的距离相等的点在角的平分线上.
应满足的条件:
(1)点在角的内部.
(2)该点到角两边的距离相等.
(2)例题:
1.下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误的是(
)
A.①
B.②
C.③
D.④
2.如图,在直角△ABC中,∠C=90?,∠CAB的平分线AD交BC于D,若DE垂直平分AB,则∠B=___.
3.如图,在△ABC中,∠CAB=90°,∠ABC=60°,BD平分∠ABC,若CD=4,则AD的长为( )
A.2
B.3
C.4
D.4.5
4.如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC= .
5、如图,在△ABC
中,D
是BC
的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,且BE=CF.
求证:AD
是△ABC
的角平分线.
6、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.
知识点7:轴对称图形及垂直平分线的性质
知识点:
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条
直线(成轴)对称.
平面内如果把一个图形沿着某一条直线折叠后,能够与另一个图形重合,那么这两个图形关于这条直线成轴对称,这条直线叫做对称轴。折叠重合的两点叫对应点也叫对称点。
(一)轴对称的性质:
成轴对称的两个图形全等。
对称轴与连结“对应点的线段”垂直。
对应点到对称轴的距离相等。
对应点的连线互相平行。
(二)用坐标表示轴对称
点(x,y)关于x轴对称的点的坐标为(x,-y);
关于X轴对称,X不变,y变相反数
点(x,y)关于y轴对称的点的坐标为(-x,y);
关于y轴对称,y不变,x变相反数
点(x,y)关于原点对称的点的坐标为(-x,-y)。关于原点轴对称,X、y都变相反数
(三)对称轴的画法:
在一个轴对称图形或成轴对称的两个图形中,连结其中一对对应点并作出所得线段的垂直平分线。
注意:有的轴对称图形只有一条对称轴,有的不止一条,要画出所有的对称轴。
成轴对称的两个图形只有一条对称轴。
我们把经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.即AP1=BP1,AP2=BP2,…
例题:
1、下列图案是轴对称图形的是(
)
B.
C.
D.
2.已知点p(m-1,4)与点Q(2,n-2)关于x轴对称,则m+n=___.
3.点(1,3)关于x轴对称的点的坐标是( )
A.(1,﹣3)
B.(﹣3,﹣1)
C.(﹣1,3)
D.(﹣1,﹣3)
4.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AB,AC于点M,N,△BCN的周长是7cm,则BC的长为( )
A.4cm
B.3
cm
C.2cm
D.1cm
5.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AB,AC于点M,N,△BCN的周长是7cm,则BC的长为( )
4cm
B.3
cm
C.2cm
D.1cm
6、如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB,BC于点D和点E.
(1)若AB=10,则△CDE的周长.
(2)若∠ACB=120?,求∠DCE的度数.
7.如图,在平面直角坐标系中,A(2,4),B(1,1),C(3,2).
(1)请画出△ABC
关于y轴对称的△A1B1C1;
(2)若△A2B2C2是△ABC
关于x轴对称的图形,请直接写出A2、B2、C2的坐标.
A2( ).
B2( ).
C2( ).
8.如图,在直角坐标系中,A(?1,5),B(?3,0),C(?4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)写出点C1的坐标。
(3)在y轴上求作点P,使PA+PB最小.
9.如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D(
),E(
),F(
);
(3)在y轴上存在一点,使PC﹣PB最大,则点P的坐标为____________.
知识点8:等腰三角形的性质和证明
(1)知识点:
(一)定理:等腰三角形有两边相等;
等腰三角形的两个底角相等
推论1:等腰三角形顶角的平分线平分底边且垂直于底边,也就是说,等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(三线合一)。
等腰三角形是以底边的垂直平分线为对称轴的轴对称图形;
推论2:等边三角形的各角相等,且每一个角都等于60°,等边三角形的三边都相等。(有三条对称轴,三线合一出现三次)
证明:有两边相等或两角相等的三角形是等腰三角形。
有一个角是60°的等腰三角形时等边三角形。
(二)30°角的直角三角形
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,反之也成立.
(2)例题:
1.如图,△ABC中,AB=AC,∠A=36?,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为(
)
A.72?
B.36?
C.60?
D.82?
2.如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )
A.30°
B.36°
C.45°
D.54°
3、定义:等腰三角形的顶角与一个底角的度数的比值称为这个等腰三角形的“特征值”,记作k,若等腰△ABC中,∠A=40°,则它的特征值k=___.
4.如图所示,已知:△ABC和△DCE都是等边三角形,求证:AD=BE.
5.如图:△ABC中,AB=AC,D为BC边的中点,DE⊥AB.
(1)求证:∠BAC=2∠EDB;
(2)若AC=6,DE=2,求△ABC的面积.
知识点1:三角形的三边
(1)知识点:
三角形任意两边之和大于第三边:b+c>a
三角形任意两边之差小于第三边:b-c
以下列数据为长度的三条线段,能组成三角形的是:(
)
A.2cm、3cm、5cm
B.2cm、3cm、4cm
C.3cm、5cm、9cm
D.8cm、4cm、4cm
2.小芳有两根长度为4cm和9cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A.3cm
B.5cm
C.12cm
D.17cm
3.一个等腰三角形的两边长分别是3和7,则它的周长为( )
A.13
B.15
C.17
D.13或17
知识点2:三角形的内角和及外角
(1)知识点:
三角形三个内角的和是180°
在直角三角形中,两个锐角互余.
三角形的一个外角等于与它不相邻的两个内角的和.
(2)例题:
1.在△ABC中,∠A:∠B:∠C=2:3:4,则∠C=____________.
2.如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是 .
3.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85°
B.80°
C.75°
D.70°
4.∠ACD是△ABC的外角,∠ACD=80°,∠B=30°,则∠A的度数为 .
5.如图,把一根直尺与一块三角尺如图放置,若么∠1=55?,则∠2的度数为___.
6.如图,在△ABC中,∠B=46?,∠C=54?,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,求∠ADE的大小。
7.如图,在△ABC中,AE是∠BAC的角平分线,AD是BC边上的高,且∠B=40°,∠C=60°,求∠EAD的度数.
8.如图,BC⊥AC于点C,CD⊥AB于点D,BE∥CD.
求证:∠EBC=∠A.
9.如图,AD为△ABC的中线,BE
为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数.
(2)在△BED中作BD边上的高,垂足为
F.若△ABC的面积为40,BD=5,则△BDE中BD边上的高EF的长为多少?
10.小明在学习过程中,对教材中的一个有趣问题做如下探究:
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
知识点3:多边形的内角和、外角和及对角线数
(1)知识点:
从n边形一个顶点可以引(n-3)条对角线,将多边形分成(n-2)个三角形。
n边形共有条对角线。
n边形的内角和等于(n-2)·180°(n≥3,n是正整数)。任意凸形多边形的外角和等于360°
(2)例题:
1.若一个多边形的内角和和外角和相加是2160°,则次多边形是(
)
A.八边形
B.十边形
C.十二边形
D.十四边形
2.一个正多边形的每个外角都等于36°,那么它是( )
A.正五边形
B.正六边形
C.正八边形
D.正十边形
3.已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )
A.6
B.7
C.8
D.9
4.一个多边形的内角和是它的外角和的4倍,这个多边形是__________边形.
知识点4:全等三角形的性质
(1)知识点:
全等的图形必须满足:(1)形状相同的图形;(2)大小相等的图形;
全等三角形的性质
(1)全等三角形对应边相等;
(2)全等三角形对应角相等;
(2)例题:
1.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
2.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2
B.3
C.5
D.2.5
知识点5:全等三角形的证明
(1)知识点:
(1)三边对应相等的两个三角形全等。(SSS)
(2)两角和它们的夹边对应相等的两个三角形全等。(ASA)
(3)两角和其中一角的对边对应相等的两个三角形全等。(AAS)
(4)两边和它们的夹角对应相等的两个三角形全等。(SAS)
(5)斜边和一条直角边对应相等的两个直角三角形全等。(HL)
(2)例题:
1.下列条件不可以判定两个直角三角形全等的是()
两条直角边对应相等
B.一条直角边和它所对的锐角对应相等
C.两个锐角对应相等
D.一个锐角和锐角所对的直角边对应相等
2.如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD,你添加的条件是
.
3.如图,已知
AB⊥BD,ED⊥BD,AB=ED,要说明△ABC≌△EDC,
①若以“SAS”为判定依据,还要添加的一个条件为 ;
②若添加条件AC=EC,则可以依据 判定全等.
4、如图,AF=CE,AD∥CB,∠B=∠D,
(1)求证:△ADF≌△CBE.
(2)若∠D=20°,∠C=25°,求∠AEB的度数.
5.已知:如图,A,E,B,D在同一直线上,AE=DB,∠A=∠D,BC∥EF.求证:△ABC≌△DEF.
6、在等边△ABC中,点D是线段BC的中点,∠EDF=120?,线段DE与线段AB相交于点E.
线段DF与线段AC相交于点F.
如图,若DF⊥AC,求∠AED的度数.
求证:DE=DF.
7.如图,在一个风筝ABCD中,AB=AD,BC=DC,分别在AB、AD的中点E、F处贴两根彩线EC、FC.
(1)∠B
与∠D相等吗?请说明理由;
(2)求证:EC=FC.
8.如图1,在线段BE上取一点C,分别以CB,CE为腰作等腰直角△BCA和等腰直角△DCE,连接BD和AE.
(1)请判断线段BD和线段AE的数量关系,并说明理由;
9、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B.
C.?E在同一条直线上,连结DC.
(1)请在图2中找出与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
10、如图,已知在△ABC中,AB=AC=10cm,BC=9cm,D为AB中点,设点P在线段BC上以3cm/s的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.
(1)若Q点运动的速度与P点相同,且点P、Q同时出发,经过1秒钟后△BPD与△CQP是否全等,并说明理由;
知识点6:角平分线的性质
(1)知识点:
①角的平分线上的点到角的两边的距离相等.
PD
=
PE.
应满足的条件:
(1)角的平分线;(2)点在角平分线上;(3)垂直距离.
②角的内部到角的两边的距离相等的点在角的平分线上.
应满足的条件:
(1)点在角的内部.
(2)该点到角两边的距离相等.
(2)例题:
1.下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误的是(
)
A.①
B.②
C.③
D.④
2.如图,在直角△ABC中,∠C=90?,∠CAB的平分线AD交BC于D,若DE垂直平分AB,则∠B=___.
3.如图,在△ABC中,∠CAB=90°,∠ABC=60°,BD平分∠ABC,若CD=4,则AD的长为( )
A.2
B.3
C.4
D.4.5
4.如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=2,ED=6,则EB+DC= .
5、如图,在△ABC
中,D
是BC
的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,且BE=CF.
求证:AD
是△ABC
的角平分线.
6、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.
知识点7:轴对称图形及垂直平分线的性质
知识点:
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条
直线(成轴)对称.
平面内如果把一个图形沿着某一条直线折叠后,能够与另一个图形重合,那么这两个图形关于这条直线成轴对称,这条直线叫做对称轴。折叠重合的两点叫对应点也叫对称点。
(一)轴对称的性质:
成轴对称的两个图形全等。
对称轴与连结“对应点的线段”垂直。
对应点到对称轴的距离相等。
对应点的连线互相平行。
(二)用坐标表示轴对称
点(x,y)关于x轴对称的点的坐标为(x,-y);
关于X轴对称,X不变,y变相反数
点(x,y)关于y轴对称的点的坐标为(-x,y);
关于y轴对称,y不变,x变相反数
点(x,y)关于原点对称的点的坐标为(-x,-y)。关于原点轴对称,X、y都变相反数
(三)对称轴的画法:
在一个轴对称图形或成轴对称的两个图形中,连结其中一对对应点并作出所得线段的垂直平分线。
注意:有的轴对称图形只有一条对称轴,有的不止一条,要画出所有的对称轴。
成轴对称的两个图形只有一条对称轴。
我们把经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.即AP1=BP1,AP2=BP2,…
例题:
1、下列图案是轴对称图形的是(
)
B.
C.
D.
2.已知点p(m-1,4)与点Q(2,n-2)关于x轴对称,则m+n=___.
3.点(1,3)关于x轴对称的点的坐标是( )
A.(1,﹣3)
B.(﹣3,﹣1)
C.(﹣1,3)
D.(﹣1,﹣3)
4.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AB,AC于点M,N,△BCN的周长是7cm,则BC的长为( )
A.4cm
B.3
cm
C.2cm
D.1cm
5.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AB,AC于点M,N,△BCN的周长是7cm,则BC的长为( )
4cm
B.3
cm
C.2cm
D.1cm
6、如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB,BC于点D和点E.
(1)若AB=10,则△CDE的周长.
(2)若∠ACB=120?,求∠DCE的度数.
7.如图,在平面直角坐标系中,A(2,4),B(1,1),C(3,2).
(1)请画出△ABC
关于y轴对称的△A1B1C1;
(2)若△A2B2C2是△ABC
关于x轴对称的图形,请直接写出A2、B2、C2的坐标.
A2( ).
B2( ).
C2( ).
8.如图,在直角坐标系中,A(?1,5),B(?3,0),C(?4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)写出点C1的坐标。
(3)在y轴上求作点P,使PA+PB最小.
9.如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D(
),E(
),F(
);
(3)在y轴上存在一点,使PC﹣PB最大,则点P的坐标为____________.
知识点8:等腰三角形的性质和证明
(1)知识点:
(一)定理:等腰三角形有两边相等;
等腰三角形的两个底角相等
推论1:等腰三角形顶角的平分线平分底边且垂直于底边,也就是说,等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(三线合一)。
等腰三角形是以底边的垂直平分线为对称轴的轴对称图形;
推论2:等边三角形的各角相等,且每一个角都等于60°,等边三角形的三边都相等。(有三条对称轴,三线合一出现三次)
证明:有两边相等或两角相等的三角形是等腰三角形。
有一个角是60°的等腰三角形时等边三角形。
(二)30°角的直角三角形
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,反之也成立.
(2)例题:
1.如图,△ABC中,AB=AC,∠A=36?,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为(
)
A.72?
B.36?
C.60?
D.82?
2.如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )
A.30°
B.36°
C.45°
D.54°
3、定义:等腰三角形的顶角与一个底角的度数的比值称为这个等腰三角形的“特征值”,记作k,若等腰△ABC中,∠A=40°,则它的特征值k=___.
4.如图所示,已知:△ABC和△DCE都是等边三角形,求证:AD=BE.
5.如图:△ABC中,AB=AC,D为BC边的中点,DE⊥AB.
(1)求证:∠BAC=2∠EDB;
(2)若AC=6,DE=2,求△ABC的面积.
同课章节目录
