人教版数学九年级上册24.1.2垂直于弦的直径课件(17张)
文档属性
| 名称 | 人教版数学九年级上册24.1.2垂直于弦的直径课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 218.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 14:49:28 | ||
图片预览



文档简介
(共17张PPT)
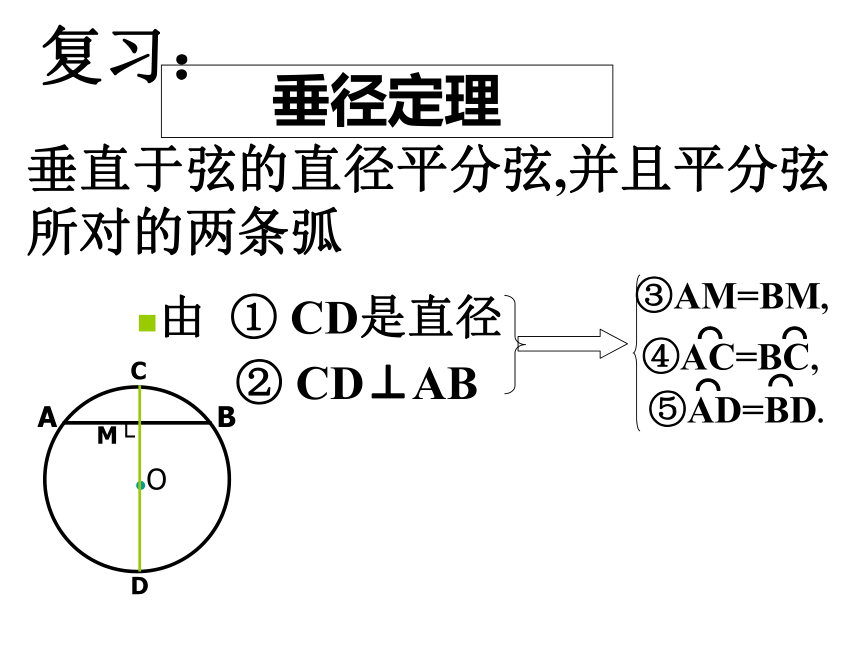
A
B
C
D
垂直于弦的直径(二)
③AM=BM,
垂径定理
●O
A
B
C
D
M└
由
①
CD是直径
②
CD⊥AB
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
复习:
垂直于弦的直径平分弦,并且平分弦
所对的两条弧
②CD⊥AB,
垂径定理的推论
●O
C
D
由
①
CD是直径
③
AM=BM
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
●
M
A
B
┗
平分弦(不是直径)的直径
垂直于弦,并且平
分弦所对
的两条弧.
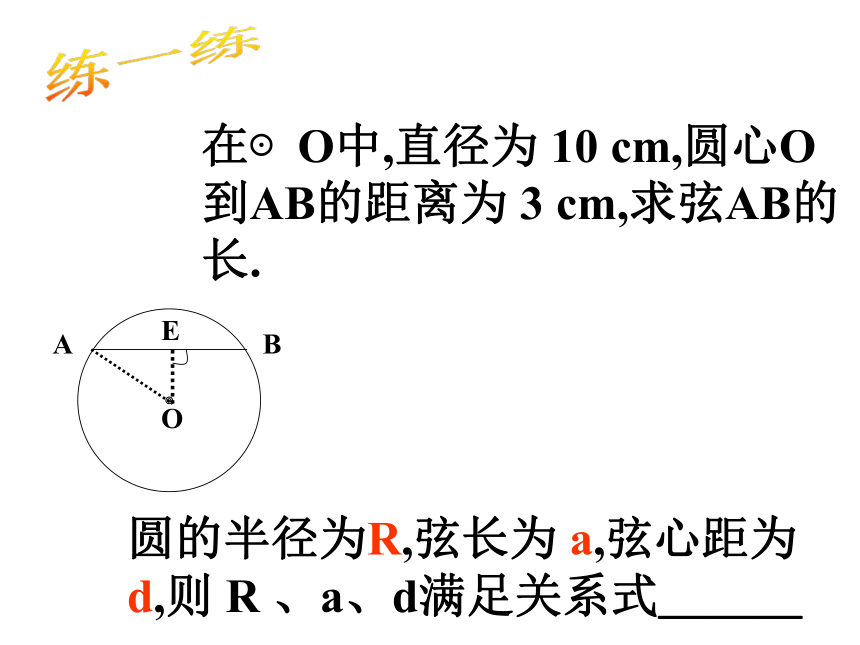
练一练
O
A
B
E
在⊙O中,直径为
10
cm,圆心O到AB的距离为
3
cm,求弦AB的长.
圆的半径为R,弦长为
a,弦心距为d,则
R
、a、d满足关系式___
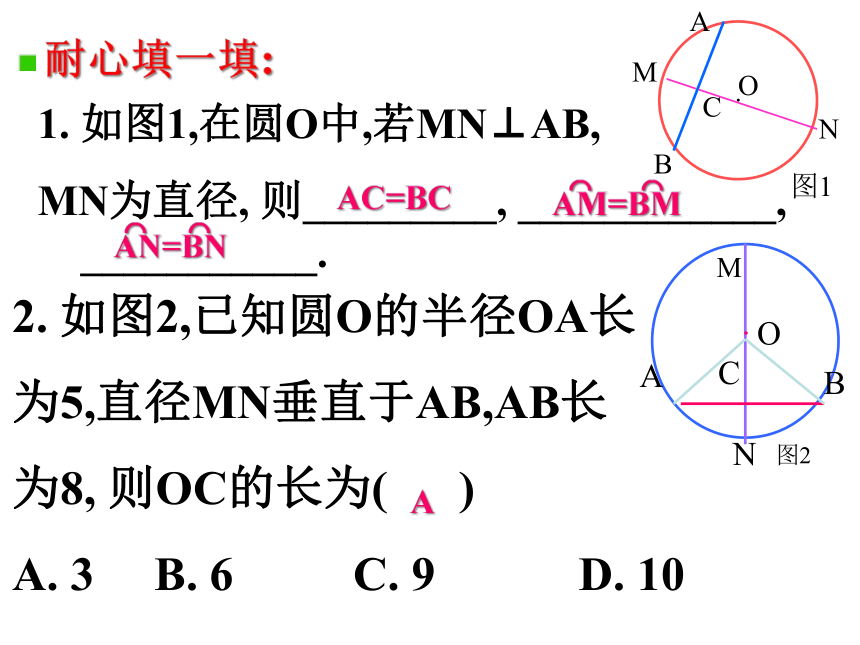
耐心填一填:
如图1,在圆O中,若MN⊥AB,
MN为直径,
则_________,
____________,
___________.
·
M
O
A
B
N
C
2.
如图2,已知圆O的半径OA长
为5,直径MN垂直于AB,AB长
为8,
则OC的长为(
)
A.
3
B.
6
C.
9
D.
10
AC=BC
A
AN=BN
⌒
⌒
AM=BM
⌒
⌒
·
M
N
O
A
B
图2
图1
C
耐心填一填:
·
M
O
A
B
N
C
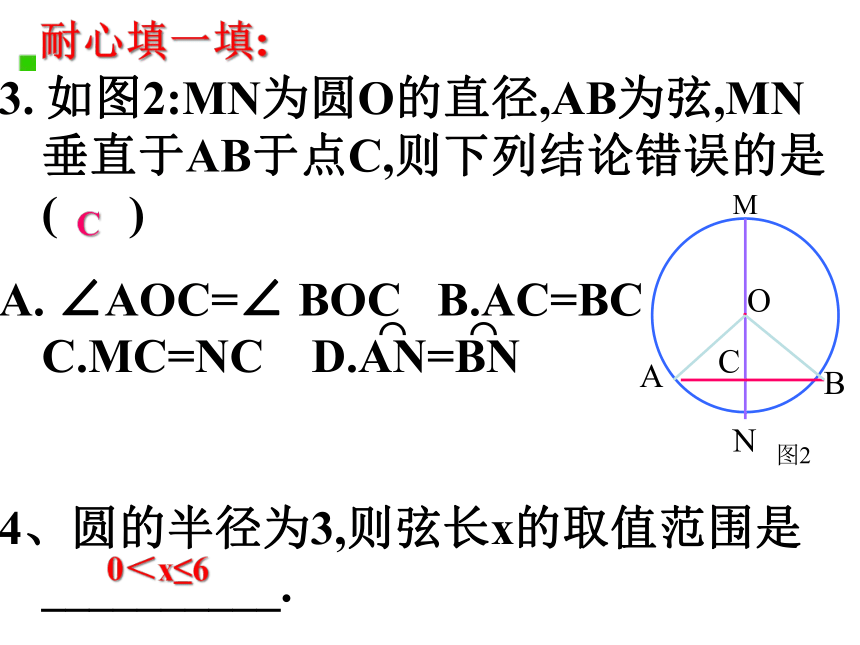
3.
如图2:MN为圆O的直径,AB为弦,MN垂直于AB于点C,则下列结论错误的是(
)
A.
∠AOC=∠
BOC
B.AC=BC
C.MC=NC
D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
C
⌒
⌒
0<x≤6
图2
5.若圆的半径为2,圆中一条弦长
为
,则此弦中点到此弦所对
劣弧的中点的距离为
多少?
例1.已知⊙O的直径是50
cm,⊙O的两条平行弦AB=40
cm
,CD=48cm,
求弦AB与CD之间的距离。
.
A
E
B
O
C
D
20
15
25
25
24
7
.
A
E
B
O
C
D
F
F
AB、CD在点O两侧
EF=OE+OF=15+7=22
AB、CD在点O同侧
EF=OE-OF=15-7=8
过点O作直线OE⊥AB,交CD于F。
练习:在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB
=
600mm,求油的最大深度.
E
D
┌
600
练习:
1.⊙O的半径为5,AB为直径,
CD为弦,垂足为E,若CD=6,
则AE的长为多少?
2.若圆心到该圆的两条平行弦的
距离分别是3和5,则此二条平行
弦之间的距离是___________.
3如图,CD为圆O的直径,
弦AB交CD于E,
∠
CEB=30°,
DE=9㎝,CE=3㎝,
求弦AB的长。
赵州石拱桥
例2:1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为
37.4
m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
R
D
37.4
7.2
解:如图,用
表示桥拱,
所在圆的圆心为O,半径为Rm,经过圆心O作弦AB的垂线OD,D为垂足,与
相交于点C.根
据垂径定理,D是AB的中点,C是
的中点,CD就是拱高.由题设
变式练习
如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.
●
O
C
D
E
F
┗
小
结
1、垂径定理及其推论
对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:
⑴d
+
h
=
r
⑵
2、要学会把实际问题转变成一
个数学问题来解决.
·
A
B
C
D
O
M
如果再交换垂径定理的题设和结论的部分语句,还会有一些什么样的结论呢?
①直线CD过圆心O
?
思考
⌒
⌒
④AC=BC,
②
CD⊥AB
③
AM=BM
⌒
⌒
⑤AD=BD.
平分弦所对的一条弧的直径,
垂直平分弦,并且并分弦所对
的另一条弧.
·
A
B
C
D
O
M
如果再交换垂径定理的题设和结论的部分语句,还会有一些什么样的结论呢?
①直线CD过圆心O
?
思考
⌒
⌒
④AC=BC,
②
CD⊥AB
③
AM=BM
⌒
⌒
⑤AD=BD.
弦的垂直平分线经过圆心,
并且并分弦所对的两条弧.
A
B
C
D
垂直于弦的直径(二)
③AM=BM,
垂径定理
●O
A
B
C
D
M└
由
①
CD是直径
②
CD⊥AB
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
复习:
垂直于弦的直径平分弦,并且平分弦
所对的两条弧
②CD⊥AB,
垂径定理的推论
●O
C
D
由
①
CD是直径
③
AM=BM
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
●
M
A
B
┗
平分弦(不是直径)的直径
垂直于弦,并且平
分弦所对
的两条弧.
练一练
O
A
B
E
在⊙O中,直径为
10
cm,圆心O到AB的距离为
3
cm,求弦AB的长.
圆的半径为R,弦长为
a,弦心距为d,则
R
、a、d满足关系式___
耐心填一填:
如图1,在圆O中,若MN⊥AB,
MN为直径,
则_________,
____________,
___________.
·
M
O
A
B
N
C
2.
如图2,已知圆O的半径OA长
为5,直径MN垂直于AB,AB长
为8,
则OC的长为(
)
A.
3
B.
6
C.
9
D.
10
AC=BC
A
AN=BN
⌒
⌒
AM=BM
⌒
⌒
·
M
N
O
A
B
图2
图1
C
耐心填一填:
·
M
O
A
B
N
C
3.
如图2:MN为圆O的直径,AB为弦,MN垂直于AB于点C,则下列结论错误的是(
)
A.
∠AOC=∠
BOC
B.AC=BC
C.MC=NC
D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
C
⌒
⌒
0<x≤6
图2
5.若圆的半径为2,圆中一条弦长
为
,则此弦中点到此弦所对
劣弧的中点的距离为
多少?
例1.已知⊙O的直径是50
cm,⊙O的两条平行弦AB=40
cm
,CD=48cm,
求弦AB与CD之间的距离。
.
A
E
B
O
C
D
20
15
25
25
24
7
.
A
E
B
O
C
D
F
F
AB、CD在点O两侧
EF=OE+OF=15+7=22
AB、CD在点O同侧
EF=OE-OF=15-7=8
过点O作直线OE⊥AB,交CD于F。
练习:在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB
=
600mm,求油的最大深度.
E
D
┌
600
练习:
1.⊙O的半径为5,AB为直径,
CD为弦,垂足为E,若CD=6,
则AE的长为多少?
2.若圆心到该圆的两条平行弦的
距离分别是3和5,则此二条平行
弦之间的距离是___________.
3如图,CD为圆O的直径,
弦AB交CD于E,
∠
CEB=30°,
DE=9㎝,CE=3㎝,
求弦AB的长。
赵州石拱桥
例2:1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为
37.4
m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
R
D
37.4
7.2
解:如图,用
表示桥拱,
所在圆的圆心为O,半径为Rm,经过圆心O作弦AB的垂线OD,D为垂足,与
相交于点C.根
据垂径定理,D是AB的中点,C是
的中点,CD就是拱高.由题设
变式练习
如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.
●
O
C
D
E
F
┗
小
结
1、垂径定理及其推论
对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:
⑴d
+
h
=
r
⑵
2、要学会把实际问题转变成一
个数学问题来解决.
·
A
B
C
D
O
M
如果再交换垂径定理的题设和结论的部分语句,还会有一些什么样的结论呢?
①直线CD过圆心O
?
思考
⌒
⌒
④AC=BC,
②
CD⊥AB
③
AM=BM
⌒
⌒
⑤AD=BD.
平分弦所对的一条弧的直径,
垂直平分弦,并且并分弦所对
的另一条弧.
·
A
B
C
D
O
M
如果再交换垂径定理的题设和结论的部分语句,还会有一些什么样的结论呢?
①直线CD过圆心O
?
思考
⌒
⌒
④AC=BC,
②
CD⊥AB
③
AM=BM
⌒
⌒
⑤AD=BD.
弦的垂直平分线经过圆心,
并且并分弦所对的两条弧.
同课章节目录
