24.2.1点和圆的位置关系
文档属性
| 名称 | 24.2.1点和圆的位置关系 |  | |
| 格式 | rar | ||
| 文件大小 | 645.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-29 10:18:15 | ||
图片预览




文档简介
(共24张PPT)
点和圆的位置关系
探究:1、请你在练习本上画一个圆,然后任意作一些点,观察这些点和圆的位置关系。
2、量一量这些点到圆心的距离。你发现了什么?
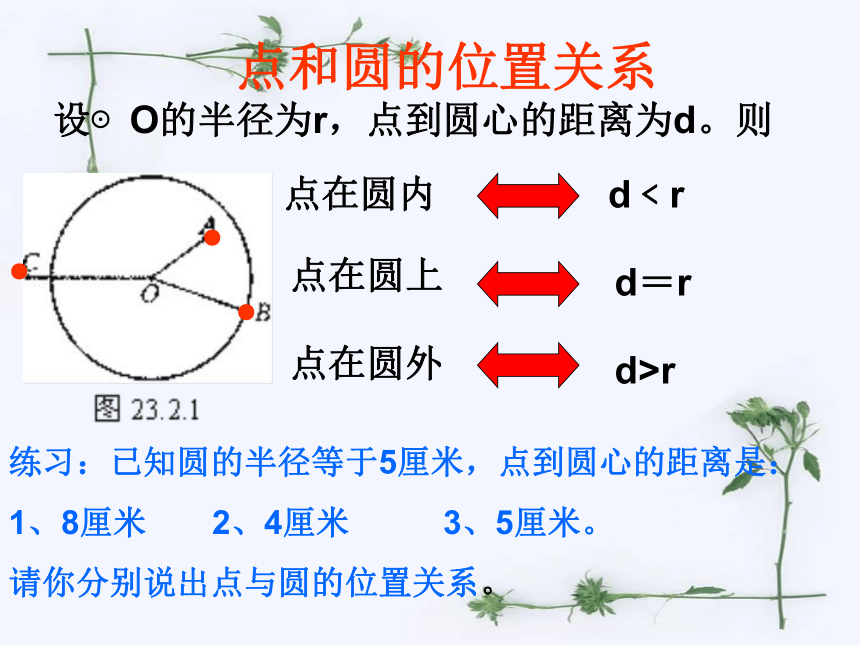
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习:已知圆的半径等于5厘米,点到圆心的距离是:
1、8厘米 2、4厘米 3、5厘米。
请你分别说出点与圆的位置关系。
●
●
●
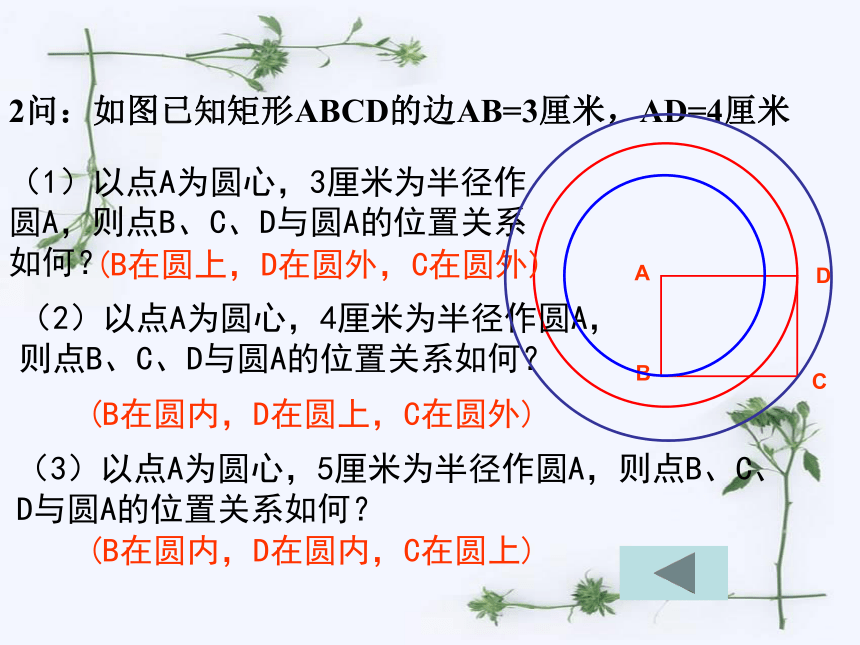
2问:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x-6x+8=0的两根,则点A与⊙O的位置关系是( )
A.点A在⊙O内部 B.点A在⊙O上
C.点A在⊙O外部 D.点A不在⊙O上
2、M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=?_____ cm.?
3、圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是( )
A、1∶2∶3∶4 B、1∶3∶2∶4
C、4∶2∶3∶1 D、4∶2∶1∶3
2
D
3
D
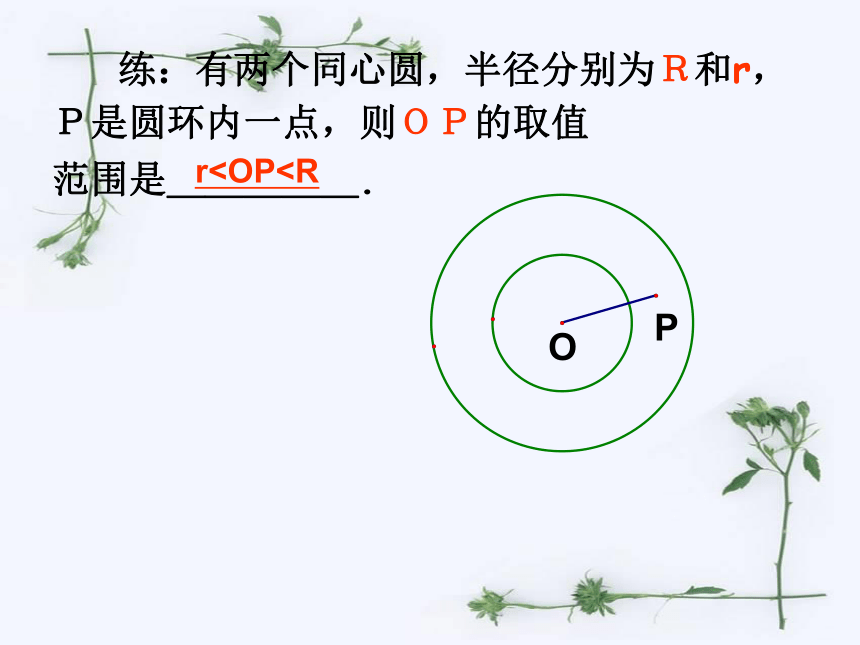
练:有两个同心圆,半径分别为R和r,
P是圆环内一点,则OP的取值
范围是_____.
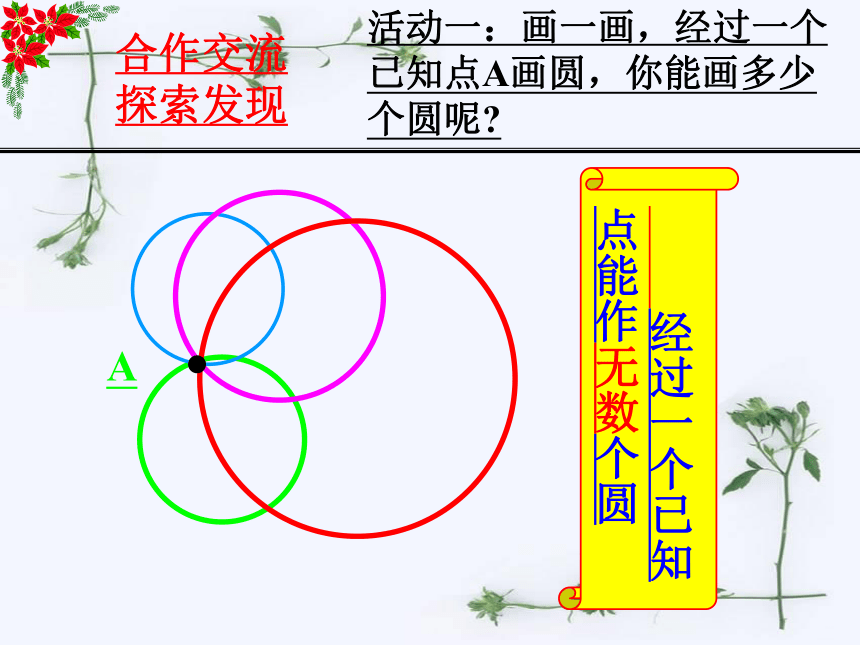
r活动一:画一画,经过一个已知点A画圆,你能画多少个圆呢
经过一个已知点能作无数个圆
合作交流探索发现
A
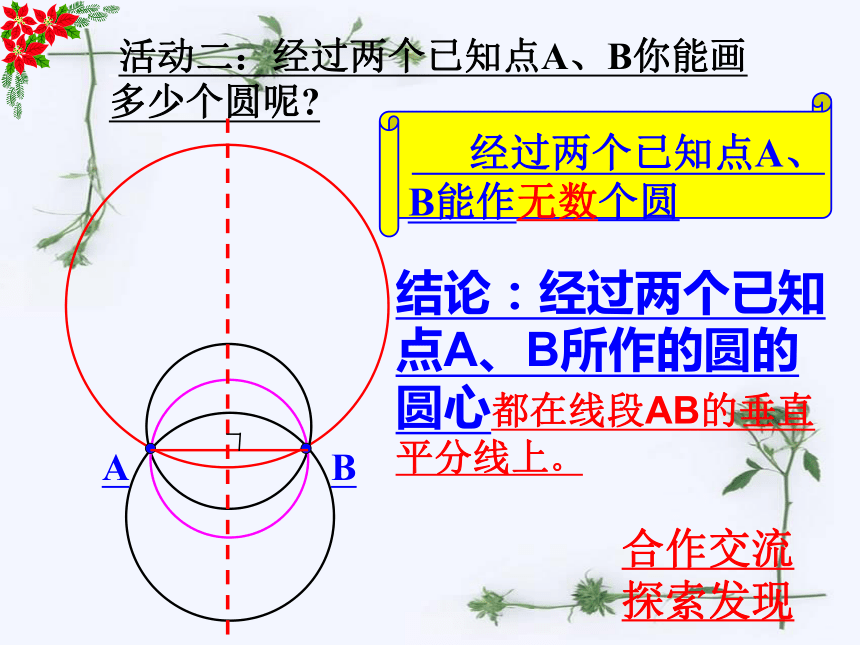
活动二:经过两个已知点A、B你能画多少个圆呢
A
B
经过两个已知点A、B能作无数个圆
结论:经过两个已知点A、B所作的圆的圆心都在线段AB的垂直平分线上。
合作交流探索发现
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离 (填“相等”或”不相等”)。
(2)连结AB、AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的 ;EF是AC的 。
(3)AB、AC的中垂线的交点O到B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
A
B
C
过如下三点能不能做圆 为什么
不在同一直线上的三点确定一个圆
反证法
例题:
已知:不在同一直线上的三点A、B、C,
求作:⊙O,使它经过点A、B、C。
做法:
1、连接AB,作线段AB的垂直平分线DE。
2、连接BC,作线段BC的垂直平分线FG,交DE于点O。
3、以O为圆心,以OB为半径作圆。
A
B
C
O
E
G
⊙O就是所求作的圆
F
D
B
A
C
O
阅读92页,完成以下填空:
如图:⊙O是△ ABC的 圆, △ ABC
是⊙O的 三角形,O是△ ABC的 心,它是 的交点,到
三角形 的距离相等。
外接
内接
外
三角形三边垂直平分线
三个顶点
●
你能画出过以下三角形的外接圆吗?(小组合作完成)
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
说一说:比较这三个三角形外心的位置,你有何发现?
证一证:你能验证图二的结论是对的吗?
(图一)
(图二)
(图三)
应用新知探索规律
总结归纳:
1.三角形的外心是三角形三边垂直平分线的交点。
2.三角形的外心到三角形三个顶点的距离相等。
3.锐角三角形的外心在三角形的内部。
直角三角形的外心是三角形的斜边中点。
钝角三角形的外心在三角形的外部。
反之成立。
应用新知探索规律
练习
例2、填空:
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )
内部
0﹤r ﹤5
外部
某居民小区的一片空地上有三颗古树,现准备在这片空地上建一个圆形广场,为使古树不被破坏,设计时要求古树恰好在圆形广场的边缘上,要怎样画出设计图呢?
确定一个圆的关键条件是什么
A
B
C
学生叙述做法
如何解决“破镜重圆”的问题:
解决问题的关键是什么?
(找圆心)
A
B
C
O
学以致用联系实际
三、思考题:
经过四个点是不是一定能作圆?
分类
1、
A
B
C
D
2、
A
B
C
D
所以经过四点不一定能作圆。
D
4、
A
B
C
A
B
C
D
3、
B
A
C
D
一.判断题:
1.过三点一定可以作圆 ( )
2.三角形有且只有一个外接圆 ( )
3.任意一个圆有一个内接三角形,并且只有
一个内接三角形 ( )
4.三角形的外心就是这个三角形任意两边垂
直平分线的交点 ( )
5.三角形的外心到三边的距离相等 ( )
6、经过不在一直线上的四点能作一个圆。( )
达标检测学情反馈
×
√
×
×
×
√
达标检测学情反馈
四.如图所示,在四边形ABCD中,∠B=∠D=90。试证明四边形ABCD有外接圆。
A
B
C
D
三. 已知△ABC中,AB=5,BC=13,AC=12,求△ABC的外接圆的面积。
如图所示,△ ABC是圆O的_____三角形;圆O是
△ ABC的_____。
2. 在Rt△ABC中,∠C=90°,AB=5cm,则其外接圆的半径为____________。
3. 已知正△ABC的边长为6cm,则其外接圆的半径为 _______ cm。
若正三长为a,则其外接圆的半径为角形的边______(用a来表示)
O
C
B
A
二. 填空题
内接
外接
2.5cm
今天我们学习了什么内容?
回顾反思
1、点和圆的位置关系:
d>r
设⊙O的半径为r,点到圆心的距离为d。则
点在圆外
d=r
d﹤r
点在圆上
点在圆内
2、不在同一直线上的三点确定一个圆
再 见!
点和圆的位置关系
探究:1、请你在练习本上画一个圆,然后任意作一些点,观察这些点和圆的位置关系。
2、量一量这些点到圆心的距离。你发现了什么?
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习:已知圆的半径等于5厘米,点到圆心的距离是:
1、8厘米 2、4厘米 3、5厘米。
请你分别说出点与圆的位置关系。
●
●
●
2问:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x-6x+8=0的两根,则点A与⊙O的位置关系是( )
A.点A在⊙O内部 B.点A在⊙O上
C.点A在⊙O外部 D.点A不在⊙O上
2、M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=?_____ cm.?
3、圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是( )
A、1∶2∶3∶4 B、1∶3∶2∶4
C、4∶2∶3∶1 D、4∶2∶1∶3
2
D
3
D
练:有两个同心圆,半径分别为R和r,
P是圆环内一点,则OP的取值
范围是_____.
r
经过一个已知点能作无数个圆
合作交流探索发现
A
活动二:经过两个已知点A、B你能画多少个圆呢
A
B
经过两个已知点A、B能作无数个圆
结论:经过两个已知点A、B所作的圆的圆心都在线段AB的垂直平分线上。
合作交流探索发现
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离 (填“相等”或”不相等”)。
(2)连结AB、AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的 ;EF是AC的 。
(3)AB、AC的中垂线的交点O到B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
A
B
C
过如下三点能不能做圆 为什么
不在同一直线上的三点确定一个圆
反证法
例题:
已知:不在同一直线上的三点A、B、C,
求作:⊙O,使它经过点A、B、C。
做法:
1、连接AB,作线段AB的垂直平分线DE。
2、连接BC,作线段BC的垂直平分线FG,交DE于点O。
3、以O为圆心,以OB为半径作圆。
A
B
C
O
E
G
⊙O就是所求作的圆
F
D
B
A
C
O
阅读92页,完成以下填空:
如图:⊙O是△ ABC的 圆, △ ABC
是⊙O的 三角形,O是△ ABC的 心,它是 的交点,到
三角形 的距离相等。
外接
内接
外
三角形三边垂直平分线
三个顶点
●
你能画出过以下三角形的外接圆吗?(小组合作完成)
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
说一说:比较这三个三角形外心的位置,你有何发现?
证一证:你能验证图二的结论是对的吗?
(图一)
(图二)
(图三)
应用新知探索规律
总结归纳:
1.三角形的外心是三角形三边垂直平分线的交点。
2.三角形的外心到三角形三个顶点的距离相等。
3.锐角三角形的外心在三角形的内部。
直角三角形的外心是三角形的斜边中点。
钝角三角形的外心在三角形的外部。
反之成立。
应用新知探索规律
练习
例2、填空:
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )
内部
0﹤r ﹤5
外部
某居民小区的一片空地上有三颗古树,现准备在这片空地上建一个圆形广场,为使古树不被破坏,设计时要求古树恰好在圆形广场的边缘上,要怎样画出设计图呢?
确定一个圆的关键条件是什么
A
B
C
学生叙述做法
如何解决“破镜重圆”的问题:
解决问题的关键是什么?
(找圆心)
A
B
C
O
学以致用联系实际
三、思考题:
经过四个点是不是一定能作圆?
分类
1、
A
B
C
D
2、
A
B
C
D
所以经过四点不一定能作圆。
D
4、
A
B
C
A
B
C
D
3、
B
A
C
D
一.判断题:
1.过三点一定可以作圆 ( )
2.三角形有且只有一个外接圆 ( )
3.任意一个圆有一个内接三角形,并且只有
一个内接三角形 ( )
4.三角形的外心就是这个三角形任意两边垂
直平分线的交点 ( )
5.三角形的外心到三边的距离相等 ( )
6、经过不在一直线上的四点能作一个圆。( )
达标检测学情反馈
×
√
×
×
×
√
达标检测学情反馈
四.如图所示,在四边形ABCD中,∠B=∠D=90。试证明四边形ABCD有外接圆。
A
B
C
D
三. 已知△ABC中,AB=5,BC=13,AC=12,求△ABC的外接圆的面积。
如图所示,△ ABC是圆O的_____三角形;圆O是
△ ABC的_____。
2. 在Rt△ABC中,∠C=90°,AB=5cm,则其外接圆的半径为____________。
3. 已知正△ABC的边长为6cm,则其外接圆的半径为 _______ cm。
若正三长为a,则其外接圆的半径为角形的边______(用a来表示)
O
C
B
A
二. 填空题
内接
外接
2.5cm
今天我们学习了什么内容?
回顾反思
1、点和圆的位置关系:
d>r
设⊙O的半径为r,点到圆心的距离为d。则
点在圆外
d=r
d﹤r
点在圆上
点在圆内
2、不在同一直线上的三点确定一个圆
再 见!
同课章节目录
