人教版数学八年级上册14.1.4同底数幂除法课件(14张)
文档属性
| 名称 | 人教版数学八年级上册14.1.4同底数幂除法课件(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 429.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 19:09:12 | ||
图片预览






文档简介
(共14张PPT)
同底数幂的除法
1/14
八上数学
人教版
教学目标
1.通过计算,观察,理解同底数幂的
除法法则;
2.理解零指数幂的意义;
3.会运用法则,熟练进行同底数幂的
除法运算;
4.培养学生逆向思维的能力.
教学重点
同底数幂的除法运算.
教学难点
逆向运用同底数幂的除法法则.
2/14
我能行
2.直接写出结果
(1)
a3
·
a4=
(2)
(-a)3
·
a4=
,
(3)(a+b)6
·
(a+b)12=
(4)
230=220
×
,
(5)
am
=a
n
·
.
1.填空
同底数幂相乘,底数
,指数
,
即am
·
an
=
(m,n都是正整数)
不变
相加
am+n
a7
-a7
(a+b)18
210
am-n
3/14
交流学
4/14
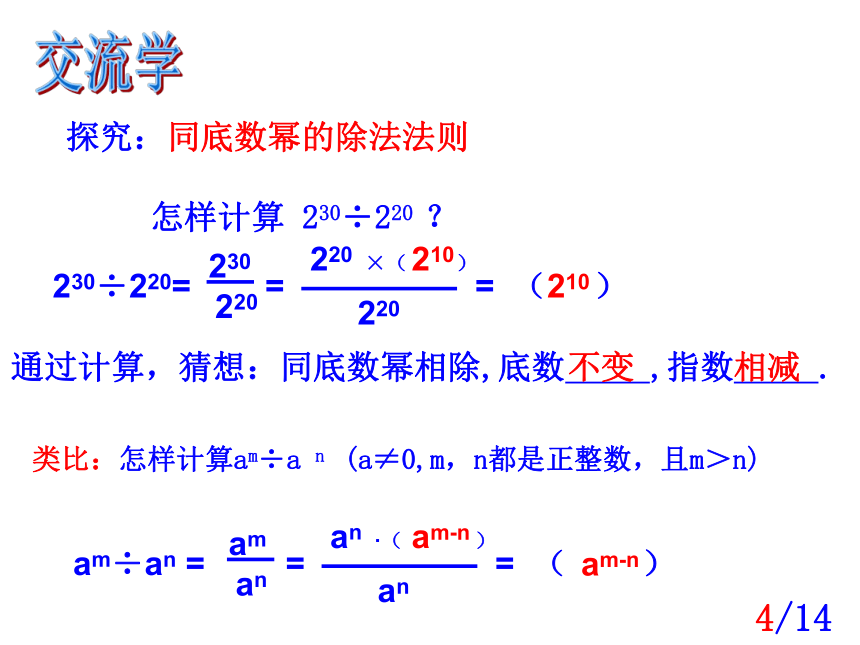
探究:同底数幂的除法法则
怎样计算
230÷220
?
类比:怎样计算am÷a
n
(a≠0,m,n都是正整数,且m>n)
230÷220=
230
220
220
×(
)
220
=
=
(
)
210
210
通过计算,猜想:同底数幂相除,底数
,指数
.
不变
相减
am÷an
=
am
an
an
·(
)
an
=
=
(
)
am-n
am-n
交流学
归纳:同底数幂的除法法则
am÷an
=
,
(a≠0,m,n都是正整数,且m>n).
文字语言叙述为:同底数幂相除,底数
,指数
.
不变
相减
am-n
5/14
交流学
尝试做
计算
1.x10÷x2
2.(xy)5÷(xy)2
3.(-x)10÷(-x)2
4.(-xy)5÷(-xy)2
6/14
交流学
变式练习
计算
1.(a-b)9÷(a-b)2
2.(a-b)9÷(b-a)2
3.(a-b)9÷(b-a)3
7/14
交流学
再探究:零指数幂的意义
由除法的意义我们可得到,
当a≠0,m为正整数时,am÷am
=
.
仿照同底数幂的除法法则
当a≠0,m为正整数时,am÷am
=am-m
=
.
通过上面两种方式的计算,你有什么猜想?
文字叙述:
的零次幂等于
.
a0
a0=1(a≠0)
1
零指数幂的意义:
任何非零数
1
8/14
交流学
尝试做
1.填空
(1)1000
=
,
(2)(-2)0
=
,
(3)(π-5)0
=
,
(4)-20150
=
.
9/14
交流学
尝试做
2.下列计算正确的是(
)
A
.
(2x-3)0=1,
B
.
a0=1,
C
.
(a2-1)0=1,
D
.
(m2+1)0=1.
D
10/14
交流学
思维拓展
1.已知
xa=32,xb=4,求xa-b的值;
2.变式练习
(2).已知
3m=5,9n=8,求32m-3n的值.
(1).已知
xm=5,xn=3,求x2m-3n的值;
11/14
学后思
学习这节课后,你有什么收获?
12/14
检测反馈
1.下列计算正确的是(
)
A.a5÷a=a5,
B.a4·a4=2a4,
C.a5÷a5=0,
D.a3÷a2=a.
2.计算:
(a8)2÷a4
(2)
(-a)10
÷a3
(3)(x-y)6÷(x-y)2
(4)
(x-y)7÷(y-x)3
(5)
x3m-1÷xm
(6)
x4m÷xn-1
3.已知:252m÷52m-1=125,求m的值;
4.已知:3m=5,9n=10,求3m-2n的值.
13/14
14/14
同底数幂的除法
1/14
八上数学
人教版
教学目标
1.通过计算,观察,理解同底数幂的
除法法则;
2.理解零指数幂的意义;
3.会运用法则,熟练进行同底数幂的
除法运算;
4.培养学生逆向思维的能力.
教学重点
同底数幂的除法运算.
教学难点
逆向运用同底数幂的除法法则.
2/14
我能行
2.直接写出结果
(1)
a3
·
a4=
(2)
(-a)3
·
a4=
,
(3)(a+b)6
·
(a+b)12=
(4)
230=220
×
,
(5)
am
=a
n
·
.
1.填空
同底数幂相乘,底数
,指数
,
即am
·
an
=
(m,n都是正整数)
不变
相加
am+n
a7
-a7
(a+b)18
210
am-n
3/14
交流学
4/14
探究:同底数幂的除法法则
怎样计算
230÷220
?
类比:怎样计算am÷a
n
(a≠0,m,n都是正整数,且m>n)
230÷220=
230
220
220
×(
)
220
=
=
(
)
210
210
通过计算,猜想:同底数幂相除,底数
,指数
.
不变
相减
am÷an
=
am
an
an
·(
)
an
=
=
(
)
am-n
am-n
交流学
归纳:同底数幂的除法法则
am÷an
=
,
(a≠0,m,n都是正整数,且m>n).
文字语言叙述为:同底数幂相除,底数
,指数
.
不变
相减
am-n
5/14
交流学
尝试做
计算
1.x10÷x2
2.(xy)5÷(xy)2
3.(-x)10÷(-x)2
4.(-xy)5÷(-xy)2
6/14
交流学
变式练习
计算
1.(a-b)9÷(a-b)2
2.(a-b)9÷(b-a)2
3.(a-b)9÷(b-a)3
7/14
交流学
再探究:零指数幂的意义
由除法的意义我们可得到,
当a≠0,m为正整数时,am÷am
=
.
仿照同底数幂的除法法则
当a≠0,m为正整数时,am÷am
=am-m
=
.
通过上面两种方式的计算,你有什么猜想?
文字叙述:
的零次幂等于
.
a0
a0=1(a≠0)
1
零指数幂的意义:
任何非零数
1
8/14
交流学
尝试做
1.填空
(1)1000
=
,
(2)(-2)0
=
,
(3)(π-5)0
=
,
(4)-20150
=
.
9/14
交流学
尝试做
2.下列计算正确的是(
)
A
.
(2x-3)0=1,
B
.
a0=1,
C
.
(a2-1)0=1,
D
.
(m2+1)0=1.
D
10/14
交流学
思维拓展
1.已知
xa=32,xb=4,求xa-b的值;
2.变式练习
(2).已知
3m=5,9n=8,求32m-3n的值.
(1).已知
xm=5,xn=3,求x2m-3n的值;
11/14
学后思
学习这节课后,你有什么收获?
12/14
检测反馈
1.下列计算正确的是(
)
A.a5÷a=a5,
B.a4·a4=2a4,
C.a5÷a5=0,
D.a3÷a2=a.
2.计算:
(a8)2÷a4
(2)
(-a)10
÷a3
(3)(x-y)6÷(x-y)2
(4)
(x-y)7÷(y-x)3
(5)
x3m-1÷xm
(6)
x4m÷xn-1
3.已知:252m÷52m-1=125,求m的值;
4.已知:3m=5,9n=10,求3m-2n的值.
13/14
14/14
