人教版八年级数学上册课件:13.2 画轴对称图形(共35张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:13.2 画轴对称图形(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 349.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
第十三章
·
轴对称
画轴对称图形
课前回顾
1、什么样的图形是轴对称图形?什么是轴对称?
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。
2、轴对称的两个图形有什么特点?
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
新课导入
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分画出整个图案?
新课导入
1.会画轴对称图形.
2.能够用轴对称的知识进行简单的图形设计.
3.理解在平面直角坐标系中,已知点关于x
轴或y
轴对称的点的坐标的变化规律.
4.掌握在平面直角坐标系中作出一个图形的轴对称图形的方法.
学习目标
自学指导
看课本P69第一自然段的内容,思考下列问题,3分钟后小组讨论
1.纸上的左脚掌印和右脚掌印是全等的吗?这两个图形有什么关系?
2.你能仿照图13.2-1再画出一只脚掌印吗?
讨论点拨
在一
张半透明的纸的左边部分,画一只左脚印,在把这张纸对折后描图,打开对折的纸。就能得到相应的右脚印,
左脚印和右脚印有什么关系?
成轴对称
对称轴是
折痕所在的
直线,既直线
l
图中的PP’与l有什么关系?
垂直平分
(1)画出的轴对称图形的形状、大小和原图形有什么
关系?
(2)画出的轴对称图形的点与原图形上的点有什么关
系?
(3)对应点所连线段与对称轴有什么关系?
小组讨论
一个平面图形和与它成轴对称的另一个图形之
间有什么关系?
由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点都是原图形上的某一点关于直线l的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
轴对称变换的性质:
讨论点拨
(1)三角形关于直线l
的对称图
形是什么形状?
(2)三角形的轴对称图形可以由
哪几个点确定?
(3)如何作一个已知点关于直线
l
的对称点?
自学指导2:
看课本P67思考及例1部分,思考下列问题,3分钟后小组讨论
例1
如图,已知△ABC
和直线l,画出与△ABC
关于直线l
对称的图形.
A
B
C
l
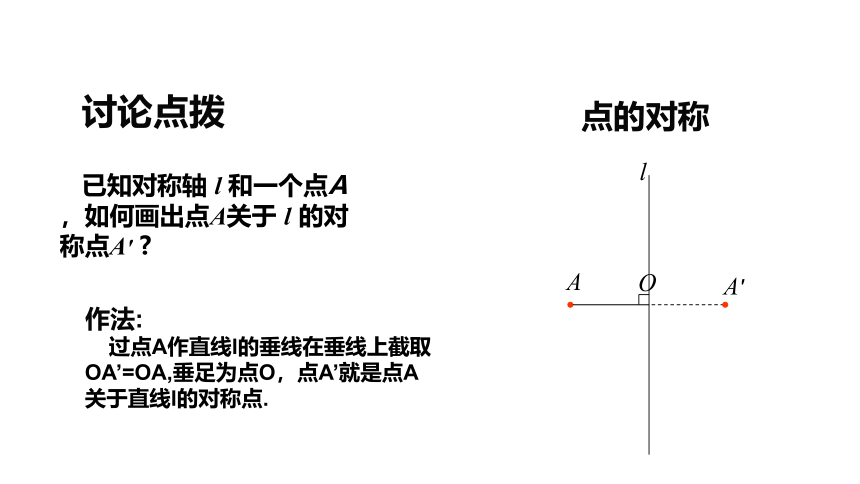
已知对称轴
l
和一个点A,如何画出点A关于
l
的对称点A′
?
A
A′
O
l
讨论点拨
作法:
过点A作直线l的垂线在垂线上截取OA’=OA,垂足为点O,点A’就是点A关于直线l的对称点.
点的对称
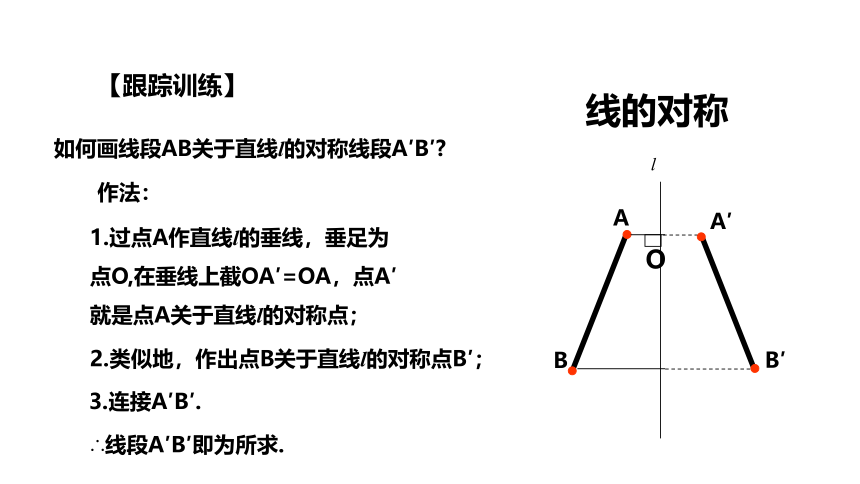
如何画线段AB关于直线l的对称线段A′B′?
A
B
A′
B′
作法:
∴线段A′B′即为所求.
O
【跟踪训练】
1.过点A作直线l的垂线,垂足为点O,在垂线上截OA′=OA,点A′就是点A关于直线l的对称点;
3.连接A′B′.
2.类似地,作出点B关于直线l的对称点B′;
线的对称
1、过点A作直线l的垂线,垂足为点O,在垂线上截OA’=OA,点A’就是点A关于直线l的对称点;
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
分析:△ABC可以由三个顶点的位置确定,只要能分别作出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要作的图形。
l
作法:
2、类似地,分别作出点B、C关于直线l的对称点B’、C’;
3、连接A’B’、B’C’、C’A’。
∴△A’B’C’即为所求.
A’
B’
C’
O
面的对称
作已知图形关于已知直线对称的图形的一般步骤:
1、找点
2、画点
3、连线
(确定图形中的一些特殊点).
(画出特殊点关于已知直线的对称点).
(连接对称点).
课堂练习
课本P68页练习
练习1 如图,把下列图形补成关于直线l
对称的图形.
l
l
l
练习2 用纸片剪一个三角形,分别沿它一边的中
线、高、角平分线对折,看看哪些部分能够重合,哪些
部分不能重合.
沿角一部分线折叠
沿高折叠
沿中线折叠
课堂练习
课本P68页练习
如
自学指导:
看课本P69思考以下的部分,完成以下问题:
(1)在直角坐标系中画出下列已知点.
A(2,-3),B(-1,2),C(-6,-5),D(
,1),E(4,
0),F
(0,-3)
(2)画出这些点分别关于x轴、y轴对称的点.并填写表格.
(3)请你仔细观察点的坐标,你能发现每对对称点的坐标有什么规律吗?
已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗?
A
A′
M
N
∴
A′就是点A关于直线MN的对称点.
O
然后延长AO至OA′,使AO=OA′.
过点A作AO⊥MN于O,
讨论点拨
·
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
A
(2,3)
你能说出点A与点A′坐标的关系吗?
如图,在平面直角坐标系中,你能画出点A关于x轴的对称点吗?
y
x
·
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
A
(2,3)
·
A′(2,-3)
点A与点A′横坐标相同,
纵坐标互为相反数.
x
y
O
讨论点拨
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
B
(-4,
2)
·
·
C(3,
-4)
关于x轴对称的点的坐标具有怎样的关系?
在平面直角坐标系中画出下列各点关于x轴的对称点.
y
x
O
讨论点拨
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
B
(-4,
2)
·
·
C(3,
-4)
·
B′
(-4,
-2)
·
C′(3,
4)
关于x轴对称的点的横坐标
相同,纵坐标互为相反数.
y
x
O
讨论点拨
·
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
A
(2,3)
·
A′
(-2,3)
你能说出点A与点A′坐标的关系吗?
如图,你能在平面直角坐标系中画出点A关于y轴的对称点吗?
y
x
O
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
B
(-4,
2)
·
·
C(3,
-4)
·
B′
(4,
2)
·
C′(-3,
-4)
关于y轴对称的点的坐标具有怎样的关系?
在平面直角坐标系中画出下列各点关于y轴的对称点.
y
x
O
关于y轴对称的点的横坐标互为相反数,
纵坐标相等.
点(x,
y)关于x轴对称的点的坐标为________.
点(x,
y)关于y轴对称的点的坐标为________.
(x,-y)
(-x,y)
讨论点拨
练习1 分别写出下列各点关于x
轴和y
轴对称的点
的坐标:(-2,6),(1,-2),(-1,3),
(-4,-2),(1,0)
.
解:关于x
轴对称的点的坐标:(-2,
-6),
(1,2),(-1,
-3),(-4,2),(1,0)
.
关于y
轴对称的点的坐标:(2,6),
(-1,-2),(1,3),(4,-2),(-1,0)
.
课堂练习
自学指导:
看课本P70例2,试着完成其中的填空和画图
例
如图,四边形ABCD
的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD
关
于x
轴和y
轴对称的图形.
x
y
1
1
O
A
B
C
D
讨论点拨
x
y
1
1
O
A
B
C
D
运用变化规律作图
解:点(x,y)关于y
轴对称的点的坐标为
(-x,y),因此四边形
ABCD
的顶点A,B,C,
D
关于y
轴对称的点分别
为:
A′(
,
),
B′(
,
),
C′(
,
),
D′(
,
),
2
5
5
1
2
1
5
4
A′
B′
C′
D′
x
y
1
1
O
A
B
C
D
运用变化规律作图
解:依次连接
,
,
,
,
就可得到与四边形ABCD
关于y轴对称的四边形
.
A′B′C′D′
A′B′
B′C′
C′D′
D′A′
A′
B′
C′
D′
请在图上画出四边形ABCD
关于x
轴对称的图形.
运用变化规律作图
x
y
1
1
O
A
B
C
D
先求出已知图形中一些特殊点(多边形的顶点)的
对称点的坐标,描出并连接这些点,就可以得到这个图
形的轴对称图形.
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线.
归纳画一个图形关于x
轴或y
轴对称的图形的方法
和步骤.
讨论点拨
4.关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
5.在平面直角坐标系中画一个图形关于x轴或y轴的对称图形:先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
1.轴对称变换的定义:
3.画已知图形关于已知直线的对称图形.
2.轴对称变换的特征;
由一个平面图形得到它的轴对称图形叫做轴对称变换.
通过本课时的学习,需要我们掌握:
第十三章
·
轴对称
画轴对称图形
课前回顾
1、什么样的图形是轴对称图形?什么是轴对称?
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。
2、轴对称的两个图形有什么特点?
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
新课导入
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分画出整个图案?
新课导入
1.会画轴对称图形.
2.能够用轴对称的知识进行简单的图形设计.
3.理解在平面直角坐标系中,已知点关于x
轴或y
轴对称的点的坐标的变化规律.
4.掌握在平面直角坐标系中作出一个图形的轴对称图形的方法.
学习目标
自学指导
看课本P69第一自然段的内容,思考下列问题,3分钟后小组讨论
1.纸上的左脚掌印和右脚掌印是全等的吗?这两个图形有什么关系?
2.你能仿照图13.2-1再画出一只脚掌印吗?
讨论点拨
在一
张半透明的纸的左边部分,画一只左脚印,在把这张纸对折后描图,打开对折的纸。就能得到相应的右脚印,
左脚印和右脚印有什么关系?
成轴对称
对称轴是
折痕所在的
直线,既直线
l
图中的PP’与l有什么关系?
垂直平分
(1)画出的轴对称图形的形状、大小和原图形有什么
关系?
(2)画出的轴对称图形的点与原图形上的点有什么关
系?
(3)对应点所连线段与对称轴有什么关系?
小组讨论
一个平面图形和与它成轴对称的另一个图形之
间有什么关系?
由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点都是原图形上的某一点关于直线l的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
轴对称变换的性质:
讨论点拨
(1)三角形关于直线l
的对称图
形是什么形状?
(2)三角形的轴对称图形可以由
哪几个点确定?
(3)如何作一个已知点关于直线
l
的对称点?
自学指导2:
看课本P67思考及例1部分,思考下列问题,3分钟后小组讨论
例1
如图,已知△ABC
和直线l,画出与△ABC
关于直线l
对称的图形.
A
B
C
l
已知对称轴
l
和一个点A,如何画出点A关于
l
的对称点A′
?
A
A′
O
l
讨论点拨
作法:
过点A作直线l的垂线在垂线上截取OA’=OA,垂足为点O,点A’就是点A关于直线l的对称点.
点的对称
如何画线段AB关于直线l的对称线段A′B′?
A
B
A′
B′
作法:
∴线段A′B′即为所求.
O
【跟踪训练】
1.过点A作直线l的垂线,垂足为点O,在垂线上截OA′=OA,点A′就是点A关于直线l的对称点;
3.连接A′B′.
2.类似地,作出点B关于直线l的对称点B′;
线的对称
1、过点A作直线l的垂线,垂足为点O,在垂线上截OA’=OA,点A’就是点A关于直线l的对称点;
例1:如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。
B
A
C
分析:△ABC可以由三个顶点的位置确定,只要能分别作出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要作的图形。
l
作法:
2、类似地,分别作出点B、C关于直线l的对称点B’、C’;
3、连接A’B’、B’C’、C’A’。
∴△A’B’C’即为所求.
A’
B’
C’
O
面的对称
作已知图形关于已知直线对称的图形的一般步骤:
1、找点
2、画点
3、连线
(确定图形中的一些特殊点).
(画出特殊点关于已知直线的对称点).
(连接对称点).
课堂练习
课本P68页练习
练习1 如图,把下列图形补成关于直线l
对称的图形.
l
l
l
练习2 用纸片剪一个三角形,分别沿它一边的中
线、高、角平分线对折,看看哪些部分能够重合,哪些
部分不能重合.
沿角一部分线折叠
沿高折叠
沿中线折叠
课堂练习
课本P68页练习
如
自学指导:
看课本P69思考以下的部分,完成以下问题:
(1)在直角坐标系中画出下列已知点.
A(2,-3),B(-1,2),C(-6,-5),D(
,1),E(4,
0),F
(0,-3)
(2)画出这些点分别关于x轴、y轴对称的点.并填写表格.
(3)请你仔细观察点的坐标,你能发现每对对称点的坐标有什么规律吗?
已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗?
A
A′
M
N
∴
A′就是点A关于直线MN的对称点.
O
然后延长AO至OA′,使AO=OA′.
过点A作AO⊥MN于O,
讨论点拨
·
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
A
(2,3)
你能说出点A与点A′坐标的关系吗?
如图,在平面直角坐标系中,你能画出点A关于x轴的对称点吗?
y
x
·
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
A
(2,3)
·
A′(2,-3)
点A与点A′横坐标相同,
纵坐标互为相反数.
x
y
O
讨论点拨
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
B
(-4,
2)
·
·
C(3,
-4)
关于x轴对称的点的坐标具有怎样的关系?
在平面直角坐标系中画出下列各点关于x轴的对称点.
y
x
O
讨论点拨
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
B
(-4,
2)
·
·
C(3,
-4)
·
B′
(-4,
-2)
·
C′(3,
4)
关于x轴对称的点的横坐标
相同,纵坐标互为相反数.
y
x
O
讨论点拨
·
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
A
(2,3)
·
A′
(-2,3)
你能说出点A与点A′坐标的关系吗?
如图,你能在平面直角坐标系中画出点A关于y轴的对称点吗?
y
x
O
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
B
(-4,
2)
·
·
C(3,
-4)
·
B′
(4,
2)
·
C′(-3,
-4)
关于y轴对称的点的坐标具有怎样的关系?
在平面直角坐标系中画出下列各点关于y轴的对称点.
y
x
O
关于y轴对称的点的横坐标互为相反数,
纵坐标相等.
点(x,
y)关于x轴对称的点的坐标为________.
点(x,
y)关于y轴对称的点的坐标为________.
(x,-y)
(-x,y)
讨论点拨
练习1 分别写出下列各点关于x
轴和y
轴对称的点
的坐标:(-2,6),(1,-2),(-1,3),
(-4,-2),(1,0)
.
解:关于x
轴对称的点的坐标:(-2,
-6),
(1,2),(-1,
-3),(-4,2),(1,0)
.
关于y
轴对称的点的坐标:(2,6),
(-1,-2),(1,3),(4,-2),(-1,0)
.
课堂练习
自学指导:
看课本P70例2,试着完成其中的填空和画图
例
如图,四边形ABCD
的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD
关
于x
轴和y
轴对称的图形.
x
y
1
1
O
A
B
C
D
讨论点拨
x
y
1
1
O
A
B
C
D
运用变化规律作图
解:点(x,y)关于y
轴对称的点的坐标为
(-x,y),因此四边形
ABCD
的顶点A,B,C,
D
关于y
轴对称的点分别
为:
A′(
,
),
B′(
,
),
C′(
,
),
D′(
,
),
2
5
5
1
2
1
5
4
A′
B′
C′
D′
x
y
1
1
O
A
B
C
D
运用变化规律作图
解:依次连接
,
,
,
,
就可得到与四边形ABCD
关于y轴对称的四边形
.
A′B′C′D′
A′B′
B′C′
C′D′
D′A′
A′
B′
C′
D′
请在图上画出四边形ABCD
关于x
轴对称的图形.
运用变化规律作图
x
y
1
1
O
A
B
C
D
先求出已知图形中一些特殊点(多边形的顶点)的
对称点的坐标,描出并连接这些点,就可以得到这个图
形的轴对称图形.
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线.
归纳画一个图形关于x
轴或y
轴对称的图形的方法
和步骤.
讨论点拨
4.关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
5.在平面直角坐标系中画一个图形关于x轴或y轴的对称图形:先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
1.轴对称变换的定义:
3.画已知图形关于已知直线的对称图形.
2.轴对称变换的特征;
由一个平面图形得到它的轴对称图形叫做轴对称变换.
通过本课时的学习,需要我们掌握:
