人教版数学八年级上册13.4 最短路径问题课件(20张)
文档属性
| 名称 | 人教版数学八年级上册13.4 最短路径问题课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 131.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
人教版《数学》八年级上册
13.4
课题学习:
最短路径问题
学习目标:
能利用“两点之间线段最短”及“连接直线外一点与直线上各点的所有线段中,垂线段最短”并结合对称、平移等变换解决最短路径问题。
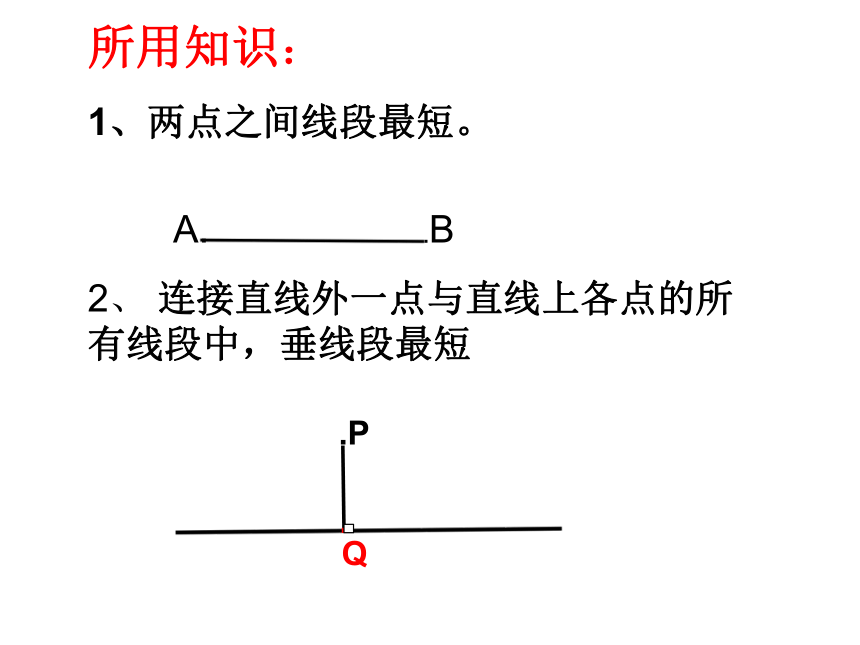
所用知识:
1、两点之间线段最短。
A.
.B
2、
连接直线外一点与直线上各点的所有线段中,垂线段最短
.P
Q
.
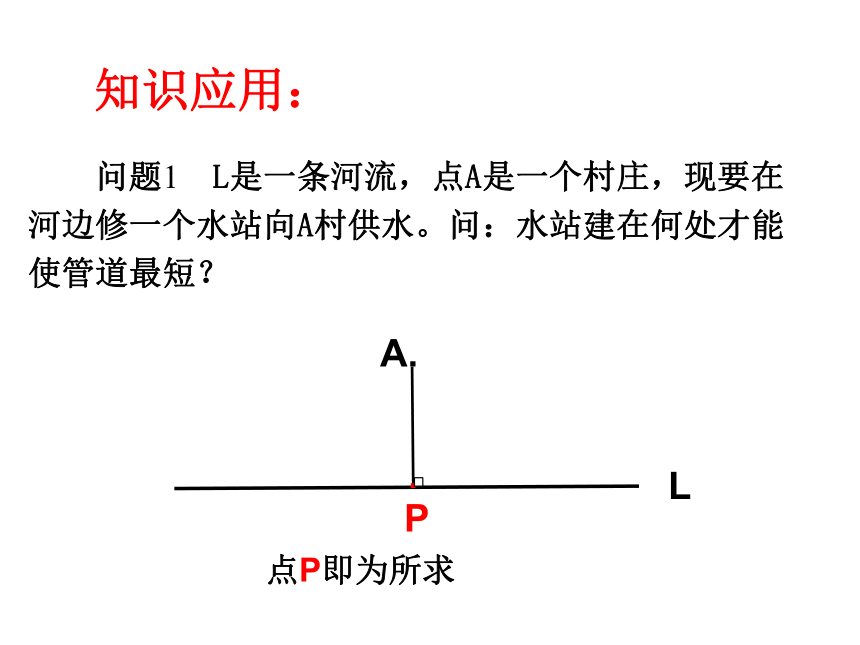
问题1 L是一条河流,点A是一个村庄,现要在
河边修一个水站向A村供水。问:水站建在何处才能
使管道最短?
L
A.
P
点P即为所求
知识应用:
.
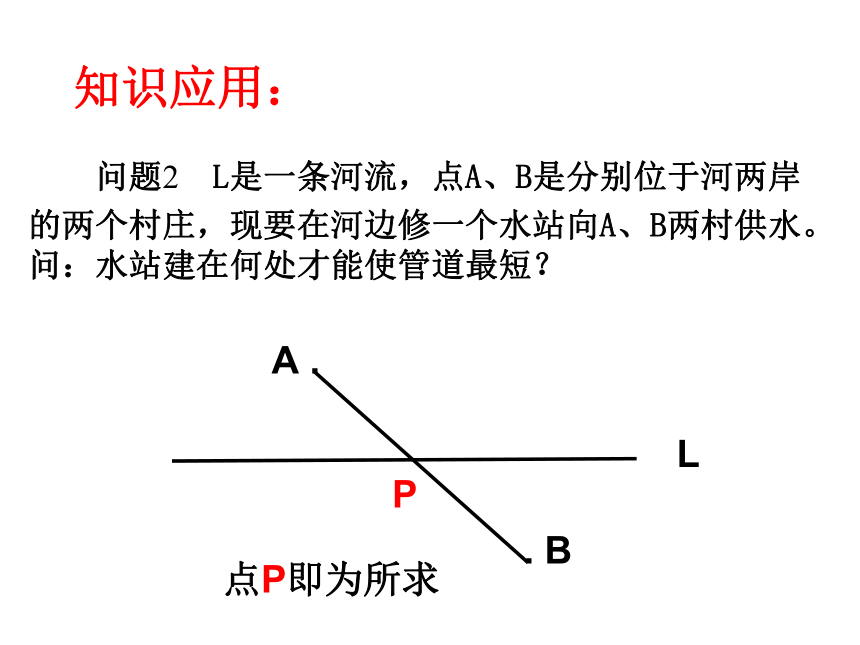
问题2 L是一条河流,点A、B是分别位于河两岸
的两个村庄,现要在河边修一个水站向A、B两村供水。问:水站建在何处才能使管道最短?
L
A
.
.
B
P
点P即为所求
知识应用:
A
.
.
B
问题3:如图,A、B两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从A到B的路径最短?(假设河的两岸是平行的直线,桥要与河岸垂直)
知识应用:
M
N
B
M
N
E
A
.
作法:1.将点B沿垂直与河岸的方向平移一个河宽到E,
2.连接AE交河对岸于点M,
则点M为建桥的位置,MN为所建的桥。
.
F.
.
证明:若桥的位置建在CD处,连接AC,
CD,DB,CE,
由平移的性质,得
BN∥EM
且BN=EM,
MN=CD,
BD∥CE,
BD=CE,
在MN处建桥:A、B两地的距离为AM+MN+BN=AM+MN+EM
=AE+MN
在CD处建桥:A、B两地的距离为:
AC+CD+DB=AC+CD+CE
=AC+CE+MN。
在△ACE中,∵AC+CE>AE,
∴AC+CE+MN>AE+MN,
即AC+CD+DB
>AM+MN+BN
所以桥的位置建在MN处,
A、B两地的路程最短。
E
B
M
N
C
D
A
F.
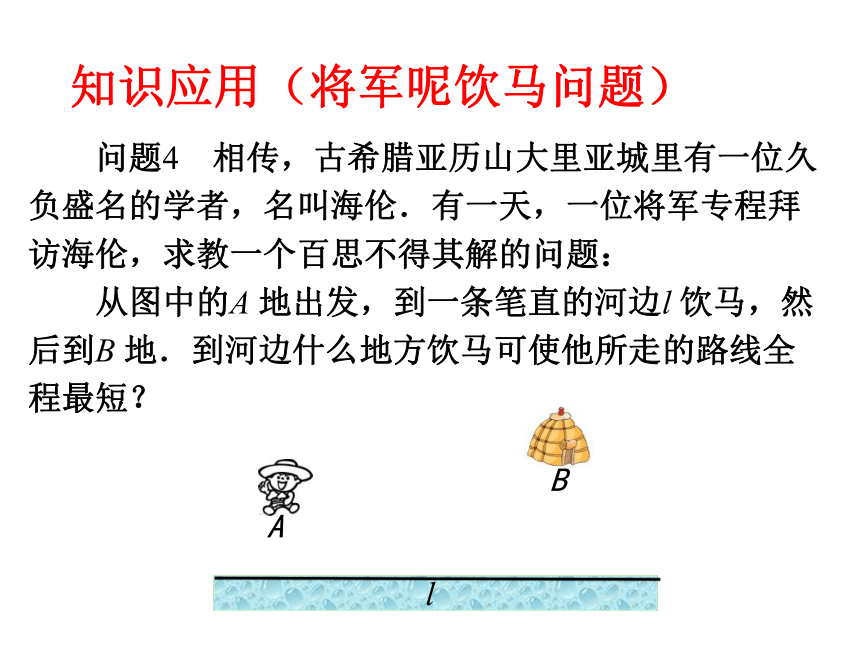
问题4 相传,古希腊亚历山大里亚城里有一位久
负盛名的学者,名叫海伦.有一天,一位将军专程拜
访海伦,求教一个百思不得其解的问题:
从图中的A
地出发,到一条笔直的河边l
饮马,然
后到B
地.到河边什么地方饮马可使他所走的路线全
程最短?
B
A
l
知识应用(将军呢饮马问题)
将A,B
两地抽象为两个点,将河l
抽象为一条直
线.
B
·
·
A
l
数学建模:
现在的问题就是怎样找出使两条线段长度之和
为最短的直线l上的点.设C
为直线上的一个动点,
上面的问题就转化为:当点C
在l
的什么位置时,
AC
与CB
的和最小.
C
作法:
(1)作点B
关于直线l
的对称
点B′;
(2)连接AB′,与直线l
相交
于点C.
则点C
即为所求.
如图,点A,B
在直线l
的同侧,点C
是直
线上的一个动点,当点C
在l
的什么位置时,
AC
与CB
的和最小?
B
·
l
A
·
B′
C
基本方法:
.
你能用所学的知识证明AC
+BC最短吗?
B
·
l
A
·
B′
C
说明理由:
.
证明:如图,在直线l
上任取一点C′(与
点C
不重合),连接AC′,BC′,B′C′
由轴对称的性质知,
BC
=B′C,BC′=B′C′
∴ AC
+BC
=
AC
+B′C
=
AB′
AC′+BC′
=
AC′+B′C′
B
·
l
A
·
B′
C
C′
在△AB′C′中,
AB′<AC′+B′C′
即 AC
+BC<AC′+BC′
因此 AC
+BC
最短
.
若直线l
上任意一点(与点
C
不重合)与A,B
两点的距离
和都大于AC
+BC,就说明AC
+
BC
最小.
B
·
l
A
·
B′
C
C′
证明AC
+BC
最短时,为什么要在直线l
上
任取一点C′(与点C
不重合),
证明AC
+BC
<AC′+BC′?
这里的“C′”的作用是什么?
思考:
.
拓展提高1:
如图,直线l是草场的边缘,直线m是河流的岸边,点A是牧场,牧羊人要先到草场放牧,再到河边饮水,最后回到牧场。问:他怎么行走才能是所走的路径最短?
l
m
.
A
A1
.
A2
.
B
C
B1.
C1.
如图,点A、B是直角坐标系中第一象限的两点,从点A出发先到达X轴在到达Y轴,最后到达B点。问:怎么行走才能使所走的路径最短?
O
X
Y
.
A
.
B
拓展提高2:
A1
.
B1
.
M
N
M1.
N1.
如图,L是一条直线,点A、B是直线同侧的两点,在直线L上求一点C,使AC与BC的差最大?
.
A
.
B
L
提高一步1:
C
c1
点C即为所求
变形:如图,L是一条直线,点A、B是直线异侧的两点,在直线L上求一点C,使AC与BC的差最大?
.
A
.
B
L
.
B1
C
C1
点C即为所求
提高一步2:
(1)本节课研究问题的基本过程是什么?
(2)轴对称、平移等数学变换在所研究问题中起什么作用?
归纳小结:
谢谢
再见
人教版《数学》八年级上册
13.4
课题学习:
最短路径问题
学习目标:
能利用“两点之间线段最短”及“连接直线外一点与直线上各点的所有线段中,垂线段最短”并结合对称、平移等变换解决最短路径问题。
所用知识:
1、两点之间线段最短。
A.
.B
2、
连接直线外一点与直线上各点的所有线段中,垂线段最短
.P
Q
.
问题1 L是一条河流,点A是一个村庄,现要在
河边修一个水站向A村供水。问:水站建在何处才能
使管道最短?
L
A.
P
点P即为所求
知识应用:
.
问题2 L是一条河流,点A、B是分别位于河两岸
的两个村庄,现要在河边修一个水站向A、B两村供水。问:水站建在何处才能使管道最短?
L
A
.
.
B
P
点P即为所求
知识应用:
A
.
.
B
问题3:如图,A、B两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从A到B的路径最短?(假设河的两岸是平行的直线,桥要与河岸垂直)
知识应用:
M
N
B
M
N
E
A
.
作法:1.将点B沿垂直与河岸的方向平移一个河宽到E,
2.连接AE交河对岸于点M,
则点M为建桥的位置,MN为所建的桥。
.
F.
.
证明:若桥的位置建在CD处,连接AC,
CD,DB,CE,
由平移的性质,得
BN∥EM
且BN=EM,
MN=CD,
BD∥CE,
BD=CE,
在MN处建桥:A、B两地的距离为AM+MN+BN=AM+MN+EM
=AE+MN
在CD处建桥:A、B两地的距离为:
AC+CD+DB=AC+CD+CE
=AC+CE+MN。
在△ACE中,∵AC+CE>AE,
∴AC+CE+MN>AE+MN,
即AC+CD+DB
>AM+MN+BN
所以桥的位置建在MN处,
A、B两地的路程最短。
E
B
M
N
C
D
A
F.
问题4 相传,古希腊亚历山大里亚城里有一位久
负盛名的学者,名叫海伦.有一天,一位将军专程拜
访海伦,求教一个百思不得其解的问题:
从图中的A
地出发,到一条笔直的河边l
饮马,然
后到B
地.到河边什么地方饮马可使他所走的路线全
程最短?
B
A
l
知识应用(将军呢饮马问题)
将A,B
两地抽象为两个点,将河l
抽象为一条直
线.
B
·
·
A
l
数学建模:
现在的问题就是怎样找出使两条线段长度之和
为最短的直线l上的点.设C
为直线上的一个动点,
上面的问题就转化为:当点C
在l
的什么位置时,
AC
与CB
的和最小.
C
作法:
(1)作点B
关于直线l
的对称
点B′;
(2)连接AB′,与直线l
相交
于点C.
则点C
即为所求.
如图,点A,B
在直线l
的同侧,点C
是直
线上的一个动点,当点C
在l
的什么位置时,
AC
与CB
的和最小?
B
·
l
A
·
B′
C
基本方法:
.
你能用所学的知识证明AC
+BC最短吗?
B
·
l
A
·
B′
C
说明理由:
.
证明:如图,在直线l
上任取一点C′(与
点C
不重合),连接AC′,BC′,B′C′
由轴对称的性质知,
BC
=B′C,BC′=B′C′
∴ AC
+BC
=
AC
+B′C
=
AB′
AC′+BC′
=
AC′+B′C′
B
·
l
A
·
B′
C
C′
在△AB′C′中,
AB′<AC′+B′C′
即 AC
+BC<AC′+BC′
因此 AC
+BC
最短
.
若直线l
上任意一点(与点
C
不重合)与A,B
两点的距离
和都大于AC
+BC,就说明AC
+
BC
最小.
B
·
l
A
·
B′
C
C′
证明AC
+BC
最短时,为什么要在直线l
上
任取一点C′(与点C
不重合),
证明AC
+BC
<AC′+BC′?
这里的“C′”的作用是什么?
思考:
.
拓展提高1:
如图,直线l是草场的边缘,直线m是河流的岸边,点A是牧场,牧羊人要先到草场放牧,再到河边饮水,最后回到牧场。问:他怎么行走才能是所走的路径最短?
l
m
.
A
A1
.
A2
.
B
C
B1.
C1.
如图,点A、B是直角坐标系中第一象限的两点,从点A出发先到达X轴在到达Y轴,最后到达B点。问:怎么行走才能使所走的路径最短?
O
X
Y
.
A
.
B
拓展提高2:
A1
.
B1
.
M
N
M1.
N1.
如图,L是一条直线,点A、B是直线同侧的两点,在直线L上求一点C,使AC与BC的差最大?
.
A
.
B
L
提高一步1:
C
c1
点C即为所求
变形:如图,L是一条直线,点A、B是直线异侧的两点,在直线L上求一点C,使AC与BC的差最大?
.
A
.
B
L
.
B1
C
C1
点C即为所求
提高一步2:
(1)本节课研究问题的基本过程是什么?
(2)轴对称、平移等数学变换在所研究问题中起什么作用?
归纳小结:
谢谢
再见
