人教版数学九年级上册 24.1圆的有关性质同步练习一(Word版 含答案)
文档属性
| 名称 | 人教版数学九年级上册 24.1圆的有关性质同步练习一(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 00:00:00 | ||
图片预览

文档简介
24.1圆的有关性质19-20年中考真题
同步练习一
一、选择题
1.(2020?青岛)如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为( )
A.99°
B.108°
C.110°
D.117°
2.(2020?滨州)在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6
B.9
C.12
D.15
3.(2020?泰安)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4
B.4
C.
D.2
4.(2019?菏泽)如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A.OC∥BD
B.AD⊥OC
C.△CEF≌△BED
D.AF=FD
5.(2019?德州)如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是( )
A.130°
B.140°
C.150°
D.160°
6.(2020?眉山)如图,四边形的外接圆为,,,,则的度数为
A.
B.
C.
D.
7.(2020?内江)如图,点、、、在上,,点是的中点,则的度数是
A.
B.
C.
D.
8.(2020?泸州)如图,中,,.则的度数为
A.
B.
C.
D.
9.(2019?眉山)如图,的直径垂直于弦,垂足是点,,,则的长为
A.
B.
C.6
D.12
10.(2020?阜新)如图,为的直径,,是圆周上的两点,若,则锐角的度数为
A.
B.
C.
D.
11.(2020?鞍山)如图,是的外接圆,半径为,若,则的度数为
A.
B.
C.
D.
12.(2020?营口)如图,为的直径,点,点是上的两点,连接,,.若,则的度数是
A.
B.
C.
D.
13.(2019?营口)如图,是的直径,,是上的两点,连接,,,若,则的度数是
A.
B.
C.
D.
14.(2019?阜新)如图,为的切线,点为切点,的延长线交于点,若,则的度数是
A.
B.
C.
D.
15.(2020?临沂)如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
二、填空题
16.(2020?襄阳)在中,若弦垂直平分半径,则弦所对的圆周角等于
.
17.(2019?随州)如图,点,,在上,点在优弧上,若,则的度数为
.
18.(2020?盐城)如图,在中,点在上,.则
.
19.(2019?无锡)如图,为的直径,点、在上,若,则的度数是
.
20.(2019?连云港)如图,点、、在上,,,则的半径为
.
21.(2019?娄底)如图,、两点在以为直径的圆上,,,则
.
22.(2019?株洲)如图所示,为的直径,点在上,且,过点的弦与线段相交于点,满足,连接,则
度.
答案:
一、选择题
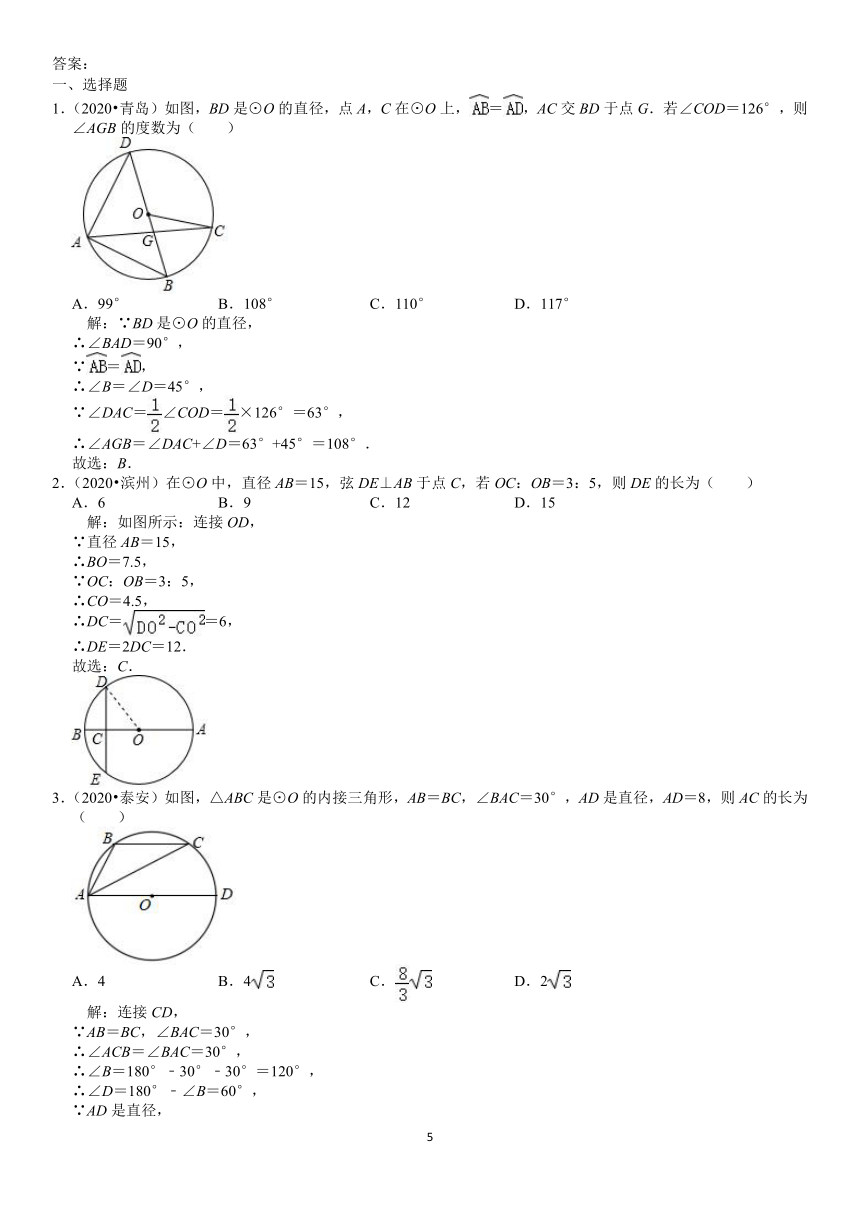
1.(2020?青岛)如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为( )
A.99°
B.108°
C.110°
D.117°
解:∵BD是⊙O的直径,
∴∠BAD=90°,
∵=,
∴∠B=∠D=45°,
∵∠DAC=∠COD=×126°=63°,
∴∠AGB=∠DAC+∠D=63°+45°=108°.
故选:B.
2.(2020?滨州)在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6
B.9
C.12
D.15
解:如图所示:连接OD,
∵直径AB=15,
∴BO=7.5,
∵OC:OB=3:5,
∴CO=4.5,
∴DC==6,
∴DE=2DC=12.
故选:C.
3.(2020?泰安)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4
B.4
C.
D.2
解:连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,
∴∠D=180°﹣∠B=60°,
∵AD是直径,
∴∠ACD=90°,
∵∠CAD=30°,AD=8,
∴CD=AD=4,
∴AC===4,
故选:B.
4.(2019?菏泽)如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A.OC∥BD
B.AD⊥OC
C.△CEF≌△BED
D.AF=FD
解:∵AB是⊙O的直径,BC平分∠ABD,
∴∠ADB=90°,∠OBC=∠DBC,
∴AD⊥BD,
∵OB=OC,
∴∠OCB=∠OBC,
∴∠DBC=∠OCB,
∴OC∥BD,选项A成立;
∴AD⊥OC,选项B成立;
∴AF=FD,选项D成立;
∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,选项C不成立;
故选:C.
5.(2019?德州)如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是( )
A.130°
B.140°
C.150°
D.160°
解:由题意得到OA=OB=OC=OD,作出圆O,如图所示,
∴四边形ABCD为圆O的内接四边形,
∴∠ABC+∠ADC=180°,
∵∠ABC=40°,
∴∠ADC=140°,
故选:B.
6.(2020?眉山)如图,四边形的外接圆为,,,,则的度数为
A.
B.
C.
D.
解:,
,
和所对的弧都是,
,
,
.
故选:.
7.(2020?内江)如图,点、、、在上,,点是的中点,则的度数是
A.
B.
C.
D.
解:连接,如图,
点是的中点,
,
.
故选:.
8.(2020?泸州)如图,中,,.则的度数为
A.
B.
C.
D.
解:,
,
,
.
故选:.
9.(2019?眉山)如图,的直径垂直于弦,垂足是点,,,则的长为
A.
B.
C.6
D.12
解:,
,
,
为等腰直角三角形,
,
.
故选:.
10.(2020?阜新)如图,为的直径,,是圆周上的两点,若,则锐角的度数为
A.
B.
C.
D.
解:连接,
是的直径,
,
,
,
.
故选:.
11.(2020?鞍山)如图,是的外接圆,半径为,若,则的度数为
A.
B.
C.
D.
解:连接和,
圆半径为2,,
,
为等边三角形,
,
,
故选:.
12.(2020?营口)如图,为的直径,点,点是上的两点,连接,,.若,则的度数是
A.
B.
C.
D.
解:如图,连接,
为的直径,
,
,
,
.
故选:.
13.(2019?营口)如图,是的直径,,是上的两点,连接,,,若,则的度数是
A.
B.
C.
D.
解:连接,如图,
是的直径,
,
,
.
故选:.
14.(2019?阜新)如图,为的切线,点为切点,的延长线交于点,若,则的度数是
A.
B.
C.
D.
解:如图:连接,
,
,
与相切于点,
,
.
故选:.
15.(2020?临沂)如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
解:连接OD、OE,
∵OC=OA,
∴△OAC是等腰三角形,
∵点D为弦AC的中点,
∴∠DOC=40°,∠BOC=100°,
设∠BOE=x,则∠COE=100°﹣x,∠DOE=100°﹣x+40°,
∵OC=OE,∠COE=100°﹣x,
∴∠OEC=∠OCE=40°+x,
∵OD<OE,∠DOE=100°﹣x+40°=140°﹣x,
∴∠OED<20°+x,
∴∠CED=∠OEC﹣∠OED>(40°+x)﹣(20°+x)=20°,
∵∠CED<∠ABC=40°,
∴20°<∠CED<40°
故选:C.
二、填空题
16.(2020?襄阳)在中,若弦垂直平分半径,则弦所对的圆周角等于 或120 .
解:如图,
弦垂直平分半径,
,
,
,
弦所对的圆周角等于或.
故答案为:或.
17.(2019?随州)如图,点,,在上,点在优弧上,若,则的度数为 .
解:,
,
,
.
故答案为.
18.(2020?盐城)如图,在中,点在上,.则 130 .
解:如图,在优弧上取一点,且异于,,连接,,
则四边形是的内接四边形,
.
,
,
,
故答案为:130.
19.(2019?无锡)如图,为的直径,点、在上,若,则的度数是 .
解:为的直径,
,
,
,
.
故答案为.
20.(2019?连云港)如图,点、、在上,,,则的半径为 6 .
解:,又,
是等边三角形
,
故答案为6.
21.(2019?娄底)如图,、两点在以为直径的圆上,,,则 1 .
解:为直径,
,
,
.
故答案为1.
22.(2019?株洲)如图所示,为的直径,点在上,且,过点的弦与线段相交于点,满足,连接,则 20 度.
解:连接,如图:
,
,
,
,
,
,
,
,
,
故答案为:20.
同步练习一
一、选择题
1.(2020?青岛)如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为( )
A.99°
B.108°
C.110°
D.117°
2.(2020?滨州)在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6
B.9
C.12
D.15
3.(2020?泰安)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4
B.4
C.
D.2
4.(2019?菏泽)如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A.OC∥BD
B.AD⊥OC
C.△CEF≌△BED
D.AF=FD
5.(2019?德州)如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是( )
A.130°
B.140°
C.150°
D.160°
6.(2020?眉山)如图,四边形的外接圆为,,,,则的度数为
A.
B.
C.
D.
7.(2020?内江)如图,点、、、在上,,点是的中点,则的度数是
A.
B.
C.
D.
8.(2020?泸州)如图,中,,.则的度数为
A.
B.
C.
D.
9.(2019?眉山)如图,的直径垂直于弦,垂足是点,,,则的长为
A.
B.
C.6
D.12
10.(2020?阜新)如图,为的直径,,是圆周上的两点,若,则锐角的度数为
A.
B.
C.
D.
11.(2020?鞍山)如图,是的外接圆,半径为,若,则的度数为
A.
B.
C.
D.
12.(2020?营口)如图,为的直径,点,点是上的两点,连接,,.若,则的度数是
A.
B.
C.
D.
13.(2019?营口)如图,是的直径,,是上的两点,连接,,,若,则的度数是
A.
B.
C.
D.
14.(2019?阜新)如图,为的切线,点为切点,的延长线交于点,若,则的度数是
A.
B.
C.
D.
15.(2020?临沂)如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
二、填空题
16.(2020?襄阳)在中,若弦垂直平分半径,则弦所对的圆周角等于
.
17.(2019?随州)如图,点,,在上,点在优弧上,若,则的度数为
.
18.(2020?盐城)如图,在中,点在上,.则
.
19.(2019?无锡)如图,为的直径,点、在上,若,则的度数是
.
20.(2019?连云港)如图,点、、在上,,,则的半径为
.
21.(2019?娄底)如图,、两点在以为直径的圆上,,,则
.
22.(2019?株洲)如图所示,为的直径,点在上,且,过点的弦与线段相交于点,满足,连接,则
度.
答案:
一、选择题
1.(2020?青岛)如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为( )
A.99°
B.108°
C.110°
D.117°
解:∵BD是⊙O的直径,
∴∠BAD=90°,
∵=,
∴∠B=∠D=45°,
∵∠DAC=∠COD=×126°=63°,
∴∠AGB=∠DAC+∠D=63°+45°=108°.
故选:B.
2.(2020?滨州)在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6
B.9
C.12
D.15
解:如图所示:连接OD,
∵直径AB=15,
∴BO=7.5,
∵OC:OB=3:5,
∴CO=4.5,
∴DC==6,
∴DE=2DC=12.
故选:C.
3.(2020?泰安)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4
B.4
C.
D.2
解:连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,
∴∠D=180°﹣∠B=60°,
∵AD是直径,
∴∠ACD=90°,
∵∠CAD=30°,AD=8,
∴CD=AD=4,
∴AC===4,
故选:B.
4.(2019?菏泽)如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A.OC∥BD
B.AD⊥OC
C.△CEF≌△BED
D.AF=FD
解:∵AB是⊙O的直径,BC平分∠ABD,
∴∠ADB=90°,∠OBC=∠DBC,
∴AD⊥BD,
∵OB=OC,
∴∠OCB=∠OBC,
∴∠DBC=∠OCB,
∴OC∥BD,选项A成立;
∴AD⊥OC,选项B成立;
∴AF=FD,选项D成立;
∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,选项C不成立;
故选:C.
5.(2019?德州)如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是( )
A.130°
B.140°
C.150°
D.160°
解:由题意得到OA=OB=OC=OD,作出圆O,如图所示,
∴四边形ABCD为圆O的内接四边形,
∴∠ABC+∠ADC=180°,
∵∠ABC=40°,
∴∠ADC=140°,
故选:B.
6.(2020?眉山)如图,四边形的外接圆为,,,,则的度数为
A.
B.
C.
D.
解:,
,
和所对的弧都是,
,
,
.
故选:.
7.(2020?内江)如图,点、、、在上,,点是的中点,则的度数是
A.
B.
C.
D.
解:连接,如图,
点是的中点,
,
.
故选:.
8.(2020?泸州)如图,中,,.则的度数为
A.
B.
C.
D.
解:,
,
,
.
故选:.
9.(2019?眉山)如图,的直径垂直于弦,垂足是点,,,则的长为
A.
B.
C.6
D.12
解:,
,
,
为等腰直角三角形,
,
.
故选:.
10.(2020?阜新)如图,为的直径,,是圆周上的两点,若,则锐角的度数为
A.
B.
C.
D.
解:连接,
是的直径,
,
,
,
.
故选:.
11.(2020?鞍山)如图,是的外接圆,半径为,若,则的度数为
A.
B.
C.
D.
解:连接和,
圆半径为2,,
,
为等边三角形,
,
,
故选:.
12.(2020?营口)如图,为的直径,点,点是上的两点,连接,,.若,则的度数是
A.
B.
C.
D.
解:如图,连接,
为的直径,
,
,
,
.
故选:.
13.(2019?营口)如图,是的直径,,是上的两点,连接,,,若,则的度数是
A.
B.
C.
D.
解:连接,如图,
是的直径,
,
,
.
故选:.
14.(2019?阜新)如图,为的切线,点为切点,的延长线交于点,若,则的度数是
A.
B.
C.
D.
解:如图:连接,
,
,
与相切于点,
,
.
故选:.
15.(2020?临沂)如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
解:连接OD、OE,
∵OC=OA,
∴△OAC是等腰三角形,
∵点D为弦AC的中点,
∴∠DOC=40°,∠BOC=100°,
设∠BOE=x,则∠COE=100°﹣x,∠DOE=100°﹣x+40°,
∵OC=OE,∠COE=100°﹣x,
∴∠OEC=∠OCE=40°+x,
∵OD<OE,∠DOE=100°﹣x+40°=140°﹣x,
∴∠OED<20°+x,
∴∠CED=∠OEC﹣∠OED>(40°+x)﹣(20°+x)=20°,
∵∠CED<∠ABC=40°,
∴20°<∠CED<40°
故选:C.
二、填空题
16.(2020?襄阳)在中,若弦垂直平分半径,则弦所对的圆周角等于 或120 .
解:如图,
弦垂直平分半径,
,
,
,
弦所对的圆周角等于或.
故答案为:或.
17.(2019?随州)如图,点,,在上,点在优弧上,若,则的度数为 .
解:,
,
,
.
故答案为.
18.(2020?盐城)如图,在中,点在上,.则 130 .
解:如图,在优弧上取一点,且异于,,连接,,
则四边形是的内接四边形,
.
,
,
,
故答案为:130.
19.(2019?无锡)如图,为的直径,点、在上,若,则的度数是 .
解:为的直径,
,
,
,
.
故答案为.
20.(2019?连云港)如图,点、、在上,,,则的半径为 6 .
解:,又,
是等边三角形
,
故答案为6.
21.(2019?娄底)如图,、两点在以为直径的圆上,,,则 1 .
解:为直径,
,
,
.
故答案为1.
22.(2019?株洲)如图所示,为的直径,点在上,且,过点的弦与线段相交于点,满足,连接,则 20 度.
解:连接,如图:
,
,
,
,
,
,
,
,
,
故答案为:20.
同课章节目录
