人教版九年级上册同步练习:24.4 弧长和扇形面积 (Word版 含解析)
文档属性
| 名称 | 人教版九年级上册同步练习:24.4 弧长和扇形面积 (Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 281.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 00:00:00 | ||
图片预览



文档简介
人教版九年级上册同步练习:24.4
弧长和扇形面积
一.选择题
1.若圆弧的半径为3,所对的圆心角为60°,则弧长为( )
A.π
B.π
C.π
D.3π
2.已知圆锥的侧面积为10πcm2,侧面展开图的圆心角为36°,则该圆锥的母线长为( )
A.100cm
B.cm
C.10cm
D.cm
3.如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )
A.9π
B.12π
C.15π
D.20π
4.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2
B.100πcm2
C.100πcm2
D.50πcm2
5.如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )
A.
B.2
C.π
D.1
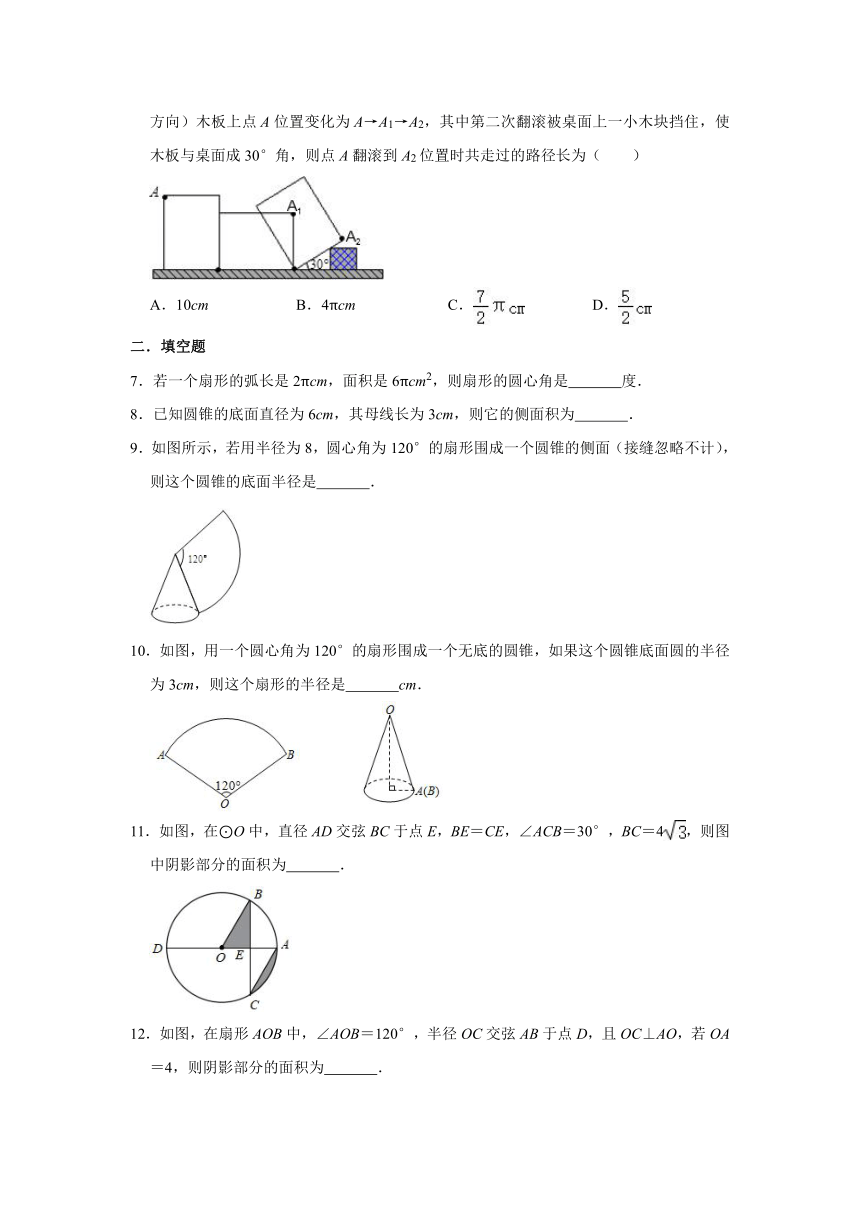
6.如图,王虎使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.10cm
B.4πcm
C.
D.
二.填空题
7.若一个扇形的弧长是2πcm,面积是6πcm2,则扇形的圆心角是
度.
8.已知圆锥的底面直径为6cm,其母线长为3cm,则它的侧面积为
.
9.如图所示,若用半径为8,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是
.
10.如图,用一个圆心角为120°的扇形围成一个无底的圆锥,如果这个圆锥底面圆的半径为3cm,则这个扇形的半径是
cm.
11.如图,在⊙O中,直径AD交弦BC于点E,BE=CE,∠ACB=30°,BC=4,则图中阴影部分的面积为
.
12.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥AO,若OA=4,则阴影部分的面积为
.
三.解答题
13.如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4米长的绳子一端拴在墙角O处(OA>4米,OB>4米),另一端栓一只小狗,小狗在地面上活动,求
(1)小狗可活动的最大区域图形的周长;
(2)小狗可活动的最大区域图形的面积(结果保留π).
14.如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°.
(1)求∠BAC的度数;
(2)当BC=4时,求劣弧AC的长.
15.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,∠A=30°,AO=1.
(1)求∠C度数;
(2)求阴影部分的面积.
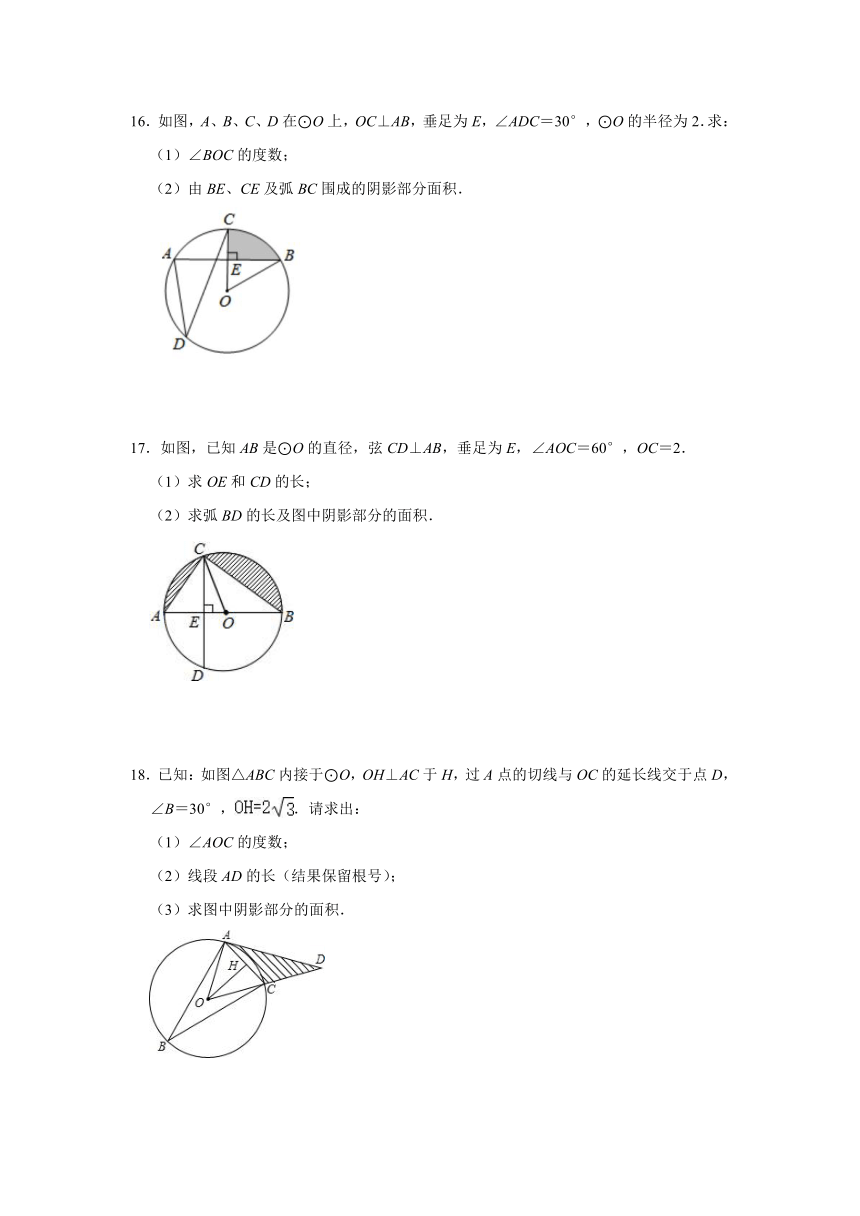
16.如图,A、B、C、D在⊙O上,OC⊥AB,垂足为E,∠ADC=30°,⊙O的半径为2.求:
(1)∠BOC的度数;
(2)由BE、CE及弧BC围成的阴影部分面积.
17.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.
(1)求OE和CD的长;
(2)求弧BD的长及图中阴影部分的面积.
18.已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,.请求出:
(1)∠AOC的度数;
(2)线段AD的长(结果保留根号);
(3)求图中阴影部分的面积.
参考答案
一.选择题
1.解:弧长l==π,
故选:B.
2.解:设母线长为Rcm,圆锥的侧面积==10π,
∴R=10
故选:C.
3.解:∵AC=4,BC=5,
∴由勾股定理得:AB=3
∴底面的周长是:6π
∴圆锥的侧面积等×6π×5=15π,
故选:C.
4.解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=10,AD=OD=10,
∴AB=2AD=20,
∴扇形围成的圆锥的侧面积==200π(cm2).
故选:A.
5.解:连接OD,
∵直径AB=2,CA切⊙O于A,
∴OB=OA=2,∠BAC=90°,
∵∠C=45°,
∴△ABC是等腰直角三角形,
∴∠B=45°,
∴∠AOD=90°,
∴S阴影=S△ABC﹣S△OBD﹣S扇形AOD+(S扇形BOD﹣S△OBD)
=S△ABC﹣2S△OBD﹣S扇形AOD+S扇形BOD
=S△ABC﹣2S△OBD
=×2×2﹣2××1×1﹣
=2﹣1
=1.
故选:D.
6.解:点A以B为旋转中心,以∠ABA1为旋转角,顺时针旋转得到A1;A2是由A1以C为旋转中心,以∠A1CA2为旋转角,顺时针旋转得到,
∵∠ABA1=90°,∠A1CA2=60°,AB==5cm,CA1=3cm,
∴点A翻滚到A2位置时共走过的路径长=+=π(cm).
故选:C.
二.填空题
7.解:设圆心角都度数为n度,
扇形的面积==6π,
解得:r=6,
又∵=2π,
∴n=60.
故答案为:60.
8.解:根据题意得,圆锥的侧面积=×6π×3=9π(cm2).
故答案为9πcm2.
9.解:设圆锥的底面半径为r,
由题意得,=2πr,
解得,r=,
故答案为:.
10.解:设扇形的半径为r,则=2π×3,
解得R=9cm.
故答案为:9.
11.解:连接AB,
∵∠ACB=30°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∵BE=CE,
∴BC⊥AO,
∴BE=CE=2,
∴OE=AE=2,
∴图中阴影部分的面积=﹣=π﹣2,
故答案为:π﹣2.
12.解:∵∠AOB=120°,OA=OB,
∴∠A=∠OBA=30°,
∵OC⊥AO,
∴∠AOD=90°,
∴∠BOD=30°,
∴DO=DB,
在Rt△AOD中,OD=OA=,OD=AD,
∴BD=AD,
∵S△AOD=×4×=,
∴S△BOD=S△AOD=
∴阴影部分的面积=S△AOD+S扇形BOC﹣S△BOD
=+﹣
=.
故答案为.
三.解答题
13.解:(1)小狗可活动的最大区域图形的周长为:=(米);
(2)小狗可活动的最大区域图形的面积为:=(米2).
答:(1)小狗可活动的最大区域图形的周长是米;
(2)小狗可活动的最大区域图形的面积是米2.
14.解:(1)∵∠ABC与∠D都是弧AC所对的圆周角,
∴∠ABC=∠D=60°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=180°﹣90°﹣60°=30°;
(2)连结OC,
∵OB=OC,∠ABC=60°∴△OBC是等边三角形
∴OC=BC=4,∠BOC=60°,
∴∠AOC=120°,
∴劣弧AC的长为=π.
15.解:(1)∵CD是圆O的直径,CD⊥AB,
∴=,
∴∠C=∠AOD,
∵∠AOD=∠COE,
∴∠C=∠COE,
∵∠A=30°,AO⊥BC,
∴∠C=30°.
(2)连接OB,
由(1)知,∠C=30°,
∴∠AOD=60°,
∴∠AOB=120°,
在Rt△AOF中,AO=1,∠AOF=60°,
∴AF=,OF=,
∴AB=,
∴S阴影=S扇形OADB﹣S△OAB=﹣××=π﹣.
16.解:(1)∵OC⊥AB,
∴,
∵∠ADC=30°,
∴∠BOC=2∠ADC=60°,
(2)∵∠BOC=60°,OC⊥AB,
∴∠OBE=30°,
∵⊙O的半径为2,
∴OE=1,BE=,
∴由BE、CE及弧BC围成的阴影部分面积=S扇形﹣S△BOE=﹣=﹣.
17.解:(1)在△OCE中,
∵∠CEO=90°,∠EOC=60°,OC=2,
∴OE=OC=1,
∴CE=OC=,
∵OA⊥CD,
∴CE=DE,
∴CD=2;
(2)∵CD⊥AB,
∴,
∵∠EOC=60°,
∴∠BOC=120°,
∴弧BD的长==,
∵S△ABC=AB?EC=×4×=2,
∴S阴影==2π﹣2.
18.解:(1)∵∠B=30°,
∴∠AOC=2∠B=60°;
(2)∵∠AOC=60°,AO=CO,
∴△AOC是等边三角形;
∵OH=,
∴AO=4;
∵AD与⊙O相切,
∴AD=;
(3)∵S扇形OAC==π,S△AOD=×4×4=8;
∴.
弧长和扇形面积
一.选择题
1.若圆弧的半径为3,所对的圆心角为60°,则弧长为( )
A.π
B.π
C.π
D.3π
2.已知圆锥的侧面积为10πcm2,侧面展开图的圆心角为36°,则该圆锥的母线长为( )
A.100cm
B.cm
C.10cm
D.cm
3.如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )
A.9π
B.12π
C.15π
D.20π
4.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2
B.100πcm2
C.100πcm2
D.50πcm2
5.如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )
A.
B.2
C.π
D.1
6.如图,王虎使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.10cm
B.4πcm
C.
D.
二.填空题
7.若一个扇形的弧长是2πcm,面积是6πcm2,则扇形的圆心角是
度.
8.已知圆锥的底面直径为6cm,其母线长为3cm,则它的侧面积为
.
9.如图所示,若用半径为8,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是
.
10.如图,用一个圆心角为120°的扇形围成一个无底的圆锥,如果这个圆锥底面圆的半径为3cm,则这个扇形的半径是
cm.
11.如图,在⊙O中,直径AD交弦BC于点E,BE=CE,∠ACB=30°,BC=4,则图中阴影部分的面积为
.
12.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥AO,若OA=4,则阴影部分的面积为
.
三.解答题
13.如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4米长的绳子一端拴在墙角O处(OA>4米,OB>4米),另一端栓一只小狗,小狗在地面上活动,求
(1)小狗可活动的最大区域图形的周长;
(2)小狗可活动的最大区域图形的面积(结果保留π).
14.如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°.
(1)求∠BAC的度数;
(2)当BC=4时,求劣弧AC的长.
15.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,∠A=30°,AO=1.
(1)求∠C度数;
(2)求阴影部分的面积.
16.如图,A、B、C、D在⊙O上,OC⊥AB,垂足为E,∠ADC=30°,⊙O的半径为2.求:
(1)∠BOC的度数;
(2)由BE、CE及弧BC围成的阴影部分面积.
17.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.
(1)求OE和CD的长;
(2)求弧BD的长及图中阴影部分的面积.
18.已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,.请求出:
(1)∠AOC的度数;
(2)线段AD的长(结果保留根号);
(3)求图中阴影部分的面积.
参考答案
一.选择题
1.解:弧长l==π,
故选:B.
2.解:设母线长为Rcm,圆锥的侧面积==10π,
∴R=10
故选:C.
3.解:∵AC=4,BC=5,
∴由勾股定理得:AB=3
∴底面的周长是:6π
∴圆锥的侧面积等×6π×5=15π,
故选:C.
4.解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=10,AD=OD=10,
∴AB=2AD=20,
∴扇形围成的圆锥的侧面积==200π(cm2).
故选:A.
5.解:连接OD,
∵直径AB=2,CA切⊙O于A,
∴OB=OA=2,∠BAC=90°,
∵∠C=45°,
∴△ABC是等腰直角三角形,
∴∠B=45°,
∴∠AOD=90°,
∴S阴影=S△ABC﹣S△OBD﹣S扇形AOD+(S扇形BOD﹣S△OBD)
=S△ABC﹣2S△OBD﹣S扇形AOD+S扇形BOD
=S△ABC﹣2S△OBD
=×2×2﹣2××1×1﹣
=2﹣1
=1.
故选:D.
6.解:点A以B为旋转中心,以∠ABA1为旋转角,顺时针旋转得到A1;A2是由A1以C为旋转中心,以∠A1CA2为旋转角,顺时针旋转得到,
∵∠ABA1=90°,∠A1CA2=60°,AB==5cm,CA1=3cm,
∴点A翻滚到A2位置时共走过的路径长=+=π(cm).
故选:C.
二.填空题
7.解:设圆心角都度数为n度,
扇形的面积==6π,
解得:r=6,
又∵=2π,
∴n=60.
故答案为:60.
8.解:根据题意得,圆锥的侧面积=×6π×3=9π(cm2).
故答案为9πcm2.
9.解:设圆锥的底面半径为r,
由题意得,=2πr,
解得,r=,
故答案为:.
10.解:设扇形的半径为r,则=2π×3,
解得R=9cm.
故答案为:9.
11.解:连接AB,
∵∠ACB=30°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∵BE=CE,
∴BC⊥AO,
∴BE=CE=2,
∴OE=AE=2,
∴图中阴影部分的面积=﹣=π﹣2,
故答案为:π﹣2.
12.解:∵∠AOB=120°,OA=OB,
∴∠A=∠OBA=30°,
∵OC⊥AO,
∴∠AOD=90°,
∴∠BOD=30°,
∴DO=DB,
在Rt△AOD中,OD=OA=,OD=AD,
∴BD=AD,
∵S△AOD=×4×=,
∴S△BOD=S△AOD=
∴阴影部分的面积=S△AOD+S扇形BOC﹣S△BOD
=+﹣
=.
故答案为.
三.解答题
13.解:(1)小狗可活动的最大区域图形的周长为:=(米);
(2)小狗可活动的最大区域图形的面积为:=(米2).
答:(1)小狗可活动的最大区域图形的周长是米;
(2)小狗可活动的最大区域图形的面积是米2.
14.解:(1)∵∠ABC与∠D都是弧AC所对的圆周角,
∴∠ABC=∠D=60°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=180°﹣90°﹣60°=30°;
(2)连结OC,
∵OB=OC,∠ABC=60°∴△OBC是等边三角形
∴OC=BC=4,∠BOC=60°,
∴∠AOC=120°,
∴劣弧AC的长为=π.
15.解:(1)∵CD是圆O的直径,CD⊥AB,
∴=,
∴∠C=∠AOD,
∵∠AOD=∠COE,
∴∠C=∠COE,
∵∠A=30°,AO⊥BC,
∴∠C=30°.
(2)连接OB,
由(1)知,∠C=30°,
∴∠AOD=60°,
∴∠AOB=120°,
在Rt△AOF中,AO=1,∠AOF=60°,
∴AF=,OF=,
∴AB=,
∴S阴影=S扇形OADB﹣S△OAB=﹣××=π﹣.
16.解:(1)∵OC⊥AB,
∴,
∵∠ADC=30°,
∴∠BOC=2∠ADC=60°,
(2)∵∠BOC=60°,OC⊥AB,
∴∠OBE=30°,
∵⊙O的半径为2,
∴OE=1,BE=,
∴由BE、CE及弧BC围成的阴影部分面积=S扇形﹣S△BOE=﹣=﹣.
17.解:(1)在△OCE中,
∵∠CEO=90°,∠EOC=60°,OC=2,
∴OE=OC=1,
∴CE=OC=,
∵OA⊥CD,
∴CE=DE,
∴CD=2;
(2)∵CD⊥AB,
∴,
∵∠EOC=60°,
∴∠BOC=120°,
∴弧BD的长==,
∵S△ABC=AB?EC=×4×=2,
∴S阴影==2π﹣2.
18.解:(1)∵∠B=30°,
∴∠AOC=2∠B=60°;
(2)∵∠AOC=60°,AO=CO,
∴△AOC是等边三角形;
∵OH=,
∴AO=4;
∵AD与⊙O相切,
∴AD=;
(3)∵S扇形OAC==π,S△AOD=×4×4=8;
∴.
同课章节目录
