人教版高中物理必修一竖直上抛专题练习含答案
文档属性
| 名称 | 人教版高中物理必修一竖直上抛专题练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 466.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-22 22:40:04 | ||
图片预览




文档简介
竖直上抛专题练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共40.0分)
做竖直上抛运动的物体( )
A.
在上升过程中,速度越来越小,加速度也越来越小
B.
在整个运动过程中,加速度大小不变方向改变
C.
上升和下降经过同一位置速度相同
D.
上升和下降经过同一段高度的过程中,上升时间等于下降时间
建筑工人常常徒手抛砖块,当砖块上升到最高点时被楼上的师傅接住用以砌墙.如所示,若某次以10
m/s的速度从地面竖直向上抛出一个砖块,g取10
m/s2,空气阻力可以忽略,则?
(???
)
A.
砖块上升的最大高度为10
m
B.
砖块上升的时间为1
s
C.
抛出后经0.5
s上升的高度为最大高度的一半
D.
抛出后上升过程砖块做加速度变化的减速直线运动
将一小球从足够高的塔顶以某初速度竖直向上抛出,经时间t=2s小球的速度大小为v=5m/s,忽略空气阻力,重力加速度g=10m/s2.则下列说法正确的是( )
A.
初速度大小一定为15m/s,2s末小球在抛出点上方10m处
B.
初速度大小一定为15m/s,2s末小球在拋出点下方10m处
C.
初速度大小可能为25m/s,2s末小球在抛出点上方30m处
D.
初速度大小可能为25m/s,2s末小球在抛出点下方30m处
将质量为m的小球甲和质量为2m的小球乙,分别从高地高度为h、2h处同时由静止释放,不计空气阻力和小球与地面碰撞的时间,碰撞后小球速度大小不变。则下列说法正确的是( )
A.
甲乙两球空中下落的加速度比之等于1:2
B.
甲乙第-次落地时速度大小之比等于1:2
C.
甲乙与地面第一次碰撞前下落的时间之比为1:2
D.
从开始下落计时时两球第一次在空中相遇
一个从地面竖直上抛的物体,它两次经过一个较低点a的时间间隔是Ta,两次经过一个较高点b的时间间隔是Tb,则a、b之间的距离为( )
A.
g(-)
B.
g(-)
C.
g(-)
D.
g(-)
一物体从某一行星表面竖直向上抛出(不计空气阻力),t=0时抛出,得到如图所示的x-t图象,则()
A.
该行星表面的重力加速度为10
m/s2
B.
该物体上升的时间为5
s
C.
该物体被抛出时的初速度为10
m/s
D.
该物体落到行星表面时的速度为20
m/s
每隔0.3s从同一高度抛出一个小球,小球做初速为6m/s的竖直上抛运动,设它们在空中不相碰.第一个小球在抛出点以上能遇到的小球数为(取g=10m/s2)( )
A.
三个
B.
四个
C.
五个
D.
六个
从地面上以初速度2υ0竖直上抛物体A,相隔时间△t后再以初速度υ0从同一地点竖直上抛物体B,不计空气阻力。以下说法正确的是(???
)
A.
物体A、B可能在物体A上升过程中相遇
B.
要使物体A、B相遇需要满足条件<△t<
C.
要使物体A、B相遇需要满足条件△t<
D.
要使物体A、B相遇需要满足条件△t>
一物体从地面以速度v竖直上抛,不计空气阻力,经过t时间到最高点,上升高度为h,则()
A.
物体通过前半程和后半程所用时间之比为1:(-1)
B.
物体通过h/2处的速度为v/2
C.
物体经过t/2时的速度为v/2
D.
物体经过前t/2和后t/2的位移之比为1:3
一个人在离地某高度处以相同的速率V0抛出两个物体A、B,A被竖直上抛,B被竖直下抛,这两个物体落地时间相差是△t,则初速度V0的大小为( )
A.
g△t
B.
g△t
C.
g△t
D.
g△t
二、多选题(本大题共5小题,共20.0分)
将一物体以的初速度竖直上拋,不计空气阻力,g取,则在第1s内物体的(????)
A.
位移大小为
B.
路程为
C.
平均速度的大小为
D.
速度改变量的大小为
如图所示,两端点分别为A、B,长L=1m的金属细杆在距地面H=40m处以v0=10m/s竖直上抛,同时在AB上方略微错开的竖直线上h处有一可视为质点的小球C由静止释放,不计空气阻力及落地后的运动,取g=10
m/s2,则可知
A.
杆从抛出到落地共用时4
s
B.
杆能上升的最大位移为10
m
C.
若h=15
m,则C与A相遇时杆的速度方向向下,与杆相遇共用时0.1
s
D.
若h=25
m,则C与A相遇时杆的速度方向向下,与杆相遇共用时0.1
s
(多选)在塔顶边缘将一物体竖直向上抛出,抛出点为A,物体上升的最大高度为20
m,不计空气阻力,g=10
m/s2,设塔足够高,则物体位移大小为10
m时,物体运动的时间可能为(
)
A.
(2-)s
B.
(2+)s
C.
(2+)s
D.
s
(多选)在地面上某处将一金属小球竖直向上抛出,上升一定高度后再落回原处。若不考虑空气阻力,则如图所示图像能正确反映小球的速度v、加速度a、位移x和速率v随时间变化关系的是(取向上为正方向)(
)
A.
B.
C.
D.
一小球自t=0时刻从水平地面上方某处自由下落,小球与地面碰后反向弹回,不计空气阻力,也不计小球与地面碰撞的时间间隔,小球距地面的高度h与运动时间t关系如图所示,取g=10m/s2.则(
)
A.
小球第一次与地面碰撞后的最大速度为10m/s
B.
小球第一次与地面碰撞后的最大速度为20m/s
C.
小球第二次与地面碰撞后上升的最大高度为1.25m
D.
小球将在t=6s时与地面发生第四次碰撞
三、计算题(本大题共3小题,共30.0分)
在一楼,有人将一物块以12
m/s的速度竖直向上抛出,物块冲过二楼窗口时被人接住,在被人接住前1
s内物块的位移是4
m,且位移方向向上,不计空气阻力,g取10
m/s2,求:
(1)人接住物块前1
s时物块的速度v
(2)物块从抛出到被人接住所经历的时间;
(3)二楼窗口距地面的高度.
气球下挂一重物,以v0=10
m/s的速度匀速上升,当到达离地高度h=175
m处时,悬挂重物的绳子突然断裂,那么重物经多长时间落到地面?落地时的速度?空气阻力不计,g取10
m/s2。
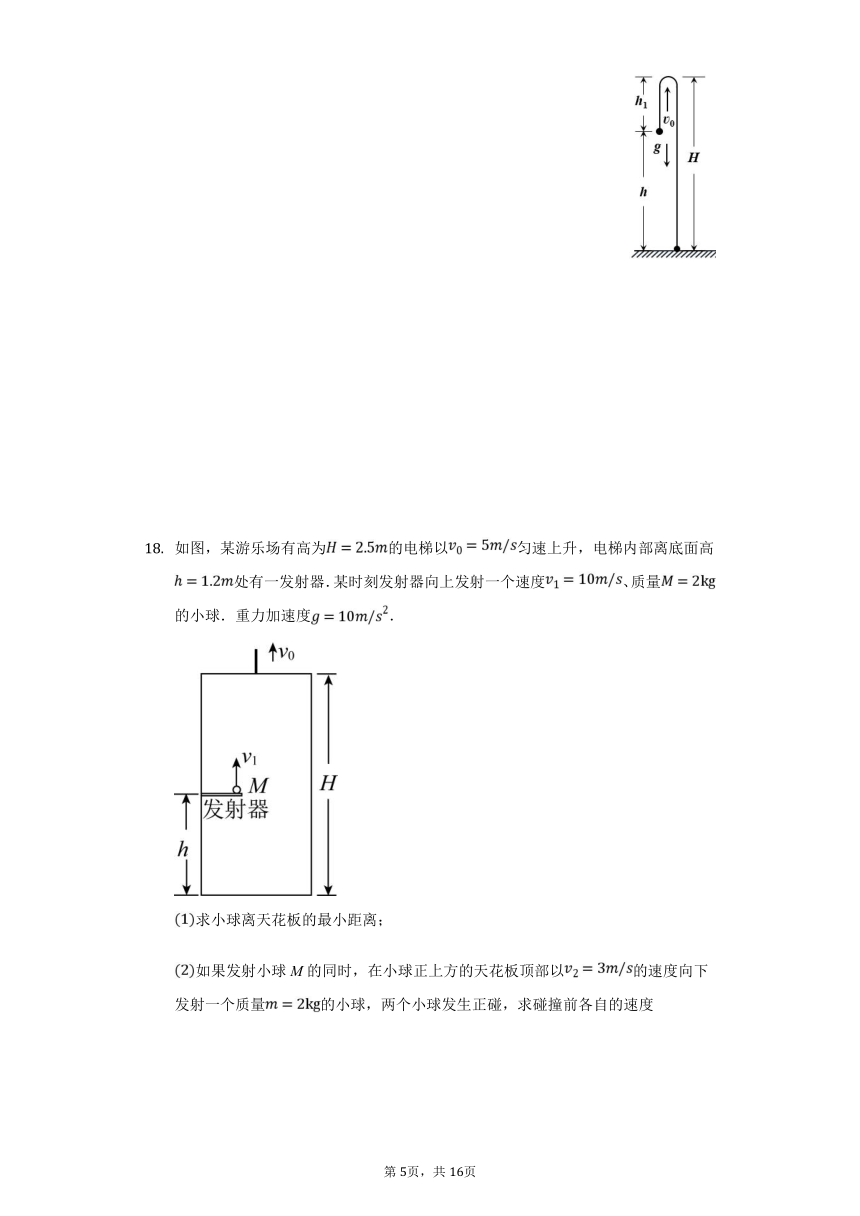
如图,某游乐场有高为的电梯以匀速上升,电梯内部离底面高处有一发射器.某时刻发射器向上发射一个速度、质量的小球.重力加速度.
求小球离天花板的最小距离;
如果发射小球M的同时,在小球正上方的天花板顶部以的速度向下发射一个质量的小球,两个小球发生正碰,求碰撞前各自的速度
答案和解析
1.【答案】D
【解析】解:A、做竖直上抛运动的物体,上升过程中速度向上,加速向下,速度减小,但加速度不变,故A错误;
B、整个运动过程中物体只受重力,加速度大小方向都不变,故B错误;
C、由对称性可知,物体回到抛出点时的速度大小不变,但方向相反,故C错误;
D、由对称性可知,向上和向下为互逆过程,上升和下降经过同一段高度的过程中时间相等,故D正确;
故选:D。
物体上升是匀减速运动,整个过程只受重力,加速度不变;由竖直上抛的对称性可知回到抛出点的速度和时间;
本题考查竖直上抛运动的规律,注意竖直上抛运动可分为向上运动和向下运动两段进行分析,而向上和向下为互逆过程,即向上的匀减速运动可看作向下的匀加速运动。
2.【答案】B
【解析】A.砖块做竖直上抛运动,上升的最大高度为,故A错误;
B.砖块上升的时间为,故B正确;
???????CD.砖块上升过程做匀减速直线运动,速度不断减小,所以前0.5s内上升的高度大于后0.5s上升的高度,则抛出后经0.5s上升的高度大于最大高度的一半,故CD错误。
故选B。
砖块做竖直上抛运动,可以看作加速度为-g的匀减速直线运动,由速度位移公式求最大高度.由速度时间公式即可求得上升的时间。
本题考查了竖直上抛运动;竖直上抛运动是常见的运动,是高考的热点,将竖直上抛运动看成一种匀减速直线运动,采用分段法研究比较好理解。
3.【答案】C
【解析】解:经时间t=2s小球的速度大小为v=5m/s,速度方向可能向上也可能向下;取向上为正;
当t=2s小球的速度为v=5m/s,则初速度v=v0-gt可得:v0=25m/s,此时小球在在抛出点上方h==m=30m处;
当t=2s小球的速度为v=-5m/s,则初速度v=v0-gt可得:v0=15m/s,此时小球在在抛出点上方h==m=10m处。故C正确、ABD错误。
故选:C。
当t=2s小球的速度为v=5m/s或速度为v=-5m/s时,求出初速度大小,再根据位移关系求解。
本题主要是考查竖直上抛运动,解答本题的关键是知道速度是一个矢量,末速度大小为5m/s,方向可能向上、可能向下。
4.【答案】D
【解析】解:A、不计空气阻力,自由落体运动的加速度与质量无关,故A错误;
B、落地速度等于v2=2gh,,高度之比等于1:2,落地时速度之比等于,故B错误;
C、下落高度与时间的关系是,显然时间之比也等于,故C错误;
D、甲球先落地,速度大小为v,此时乙球速度也为v,乙球也下落了h,设再过一段时间△t,二者在空中相遇,则有:,而甲球下落h的时间为故第一次相遇的时刻为,故D正确。
故选:D。
两小球均做自由落体运动,根据自由落体运动规律可确定加速度、速度以及时间关系;再分析两球的运动过程,根据运动学公式确定相遇时间。
本题考查自由落体运动以及竖直上抛运动规律,要注意两球在空中均做自由落体运动;但由于下落高度不同,故距离h的小球落地反弹后与球乙相遇。
5.【答案】B
【解析】解:小球做竖直上抛运动,根据运动时间的对称性得,物体从最高点自由下落到A点的时间为,物体从最高点自由下落到B点的时间为,
竖直上抛运动的加速度a=g,由x=at2可得:
最高点到A点的距离为:xA=gTa2…①
最高点到B点的距离为:xB=gTb2…②
A点在B点下方,由①、②解得,AB相距为:
△x=g(Ta2-Tb2)。
故选:B。
因为是上抛运动可以利用对称来解,可以得到物体从顶点到a的时间为,顶点到B点的时间为,
从顶点出发初速度为0,经过t时间到达某个点,位移式x=at2将其带入求解.
竖直上抛上去和下来具有对称性,所需的时间是一样的,所以只要讨论下来就可以,在最高点速度是0,就是个初速度为0的匀加速运动.
6.【答案】D
【解析】
【分析】
物体从行星表面竖直上抛,由图读出最大高度和上升的时间,根据运动学公式求出初速度和重力加速度。物体落回行星表面的速度与抛出时速度大小相等。
本题首先考查读图能力,图上能读出最大高度、上升和下落时间等等;其次要灵活选择运动学公式求解。
【解答】
ABC.由图读出,物体上升的最大高度为h=25m,上升的时间为t=2.5s,
对于上升过程,有h=得,初速度v0==m/s=20m/s,
物体上升的加速度大小a=g==m/s2=8m/s2,故ABC错误;
D.根据对称性可知,该物体落到行星表面时的速度大小与初速度大小相等,也为20m/s,故D正确。
故选D。
7.【答案】A
【解析】解:小球做竖直上抛运动,从抛出到落地的整个过程是匀变速运动,根据位移时间关系公式,有:
x=v0t-gt2
代入数据,有:
0=6t-×10×t2
解得:t=0(舍去)或
t=1.2s
每隔0.3s抛出一个小球,故第一个小球在抛出点以上能遇到的小球数为:
N=-1=3
故选:A。
小球做竖直上抛运动,先求解出小球运动的总时间,然后判断小球在抛出点以上能遇到的小球数.
本题关键明确第一个小球的运动情况,然后选择恰当的运动学公式列式求解出运动时间,再判断相遇的小球个数.
8.【答案】B
【解析】
【分析】
两个物体空中都做竖直上抛运动,相遇可能有几种情况:①A、B均在下降,A追上B;②A在下降,B在上升。根据运动学规律求出两物体在空中运动的总时间,两物体抛出的时间间隔Δt必须满足条件:①抛出B时A不能已经落地;②B不能先落地,即A在B前落.由此分析间隔Δt必须满足条件。
本题关键要判断出物体A、B只能在物体A下降过程中相遇,根据两球运动的总时间关系,分析抛出时的时间间隔。
【解答】
A.A物体上升时,A的初速度大于B的初速度,且A先抛出,所以A的位移大于B的位移,不可能在A上升的过程中相遇,故A错误;
BCD.A在空中的总时间为t1=2×=;B在空中的总时间为t2=,要使A、B能在空中相遇,t1-t2<Δt<t1,即得:<Δt<,故B正确,CD错误。
故选B。
9.【答案】C
【解析】
【分析】
物体做竖直上抛运动,其逆运动为自由落体运动,初速度为零;由匀变速直线运动的规律进行分析解答。
本题考查自由落体的运动规律,要注意明确自由落体就是初速度为零,加速度为g的匀加速直线运动;所有运动学公式及结论均可以使用。
【解答】
解:A、设全程高度为h,则由位移公式可知,h=gt2;则前半程的时间t1=;全程的时间t=;则后半程所用时间为t2=t-t1=;因本题为上抛运动,为自由落体的逆运动,故前后半程内的时间之比为:():1;故A错误;
B、由v2=2gh可得,通过时的速度为,落地时的速度为:,故,故B错误;
C、由v=gt可得,物体通过时的速度v=g=,故C正确;
D、做自由落体运动时,前一半时间内的平均速度为;而后一半时间内的平均速度为;本题为竖直上抛运动,故前后一半时间内的速度之比为3:1;故D错误;
故选C。
10.【答案】B
【解析】解:根据机械能守恒可知两个物体落地时的速度大小相等,设为v。
对于竖直上抛,取竖直向上为正方向,则有t1==
对于竖直下抛,有t2=
据题△t=t1-t2=
则v0=g△t
故选:B。
竖直下抛是匀加速直线运动,竖直上抛是匀减速直线运动,根据速度位移公式分别列式两个运动的时间,即可求解。
本题关键要熟练运用运动学速度时间公式列出时间表达式,要注意取竖直向上为正方向时,竖直上抛运动的加速度为-g,落地时速度大小为-v。
11.【答案】BCD
【解析】
【分析】
物体竖直上抛后,只受重力,加速度等于重力加速度,可以把物体的运动看成一种匀减速直线运动,由位移公式求出1s内位移,由平均速度公式求出平均速度,由△v=at求出速度的改变量。对于竖直上抛运动,通常有两种处理方法,一种是分段法,一种是整体法,两种方法可以交叉运用。
【解答】
?A、1s内物体的位移为:x=m=3m,方向竖直向上,故A错误;
B、物体上升的最大位移为:m,物体上升和下落的总路程为3.2m+(3.2-3.0)m=3.4m,所以1s内的路程是3.4m,故B正确;
C、平均速度:=m/s.故C正确;
D、速度改变量的大小为:△v=at=gt=10×1m/s=10m/s。故D正确。
故选:BCD
12.【答案】ACD
【解析】略
13.【答案】ABC
【解析】[解析] 物体在塔顶边缘的A点抛出,位移大小为10
m的位置有两处,如图所示,一处在A点之上,另一处在A点之下,在A点之上时,通过位移大小为10
m处有上升和下降两种过程,在A点之下10
m处只有下降过程。
法一:分段法
由H=,得v0=20
m/s,
物体上升10
m时,速度为v1,则由v12-v02=-2gh,
得v1=10?m/s,
则t1==(2-)s,故A对;
物体从抛出到下落至A点上方10
m时,
t2=t1+=(2+)s,故B对;
物体从最高点到下落至A点下方10
m处时,
H+h=gt32,则t3=?s,
故物体从抛出到下落至A点下方10
m处时,
t3′=+t3=(2+)s,故C对,D错。
法二:全程法
取竖直向上为正方向,物体的位移为x=v0t-gt2,
当物体位于A点上方10
m处时x=10
m,
解得t1=(2-)s,t2=(2+)s,故选项A、B对。
当物体位于A点下方10
m处时,x=-10
m,
解得t3=(2+)s,另一解为负值,舍去,故选项C对,D错。
[答案]ABC
14.【答案】AD
【解析】金属小球做竖直上抛运动,上升和下降过程加速度大小和方向都不变,做匀变速直线运动,速度图像应是倾斜的直线。以向上为正方向,速度先正后负,加速度为负值,A正确,B错误;上升过程速率均匀减小,下降过程速率均匀增加,D正确;根据位移时间关系式:x=v0t+at2可知位移时间图像是抛物线,C错误。故选AD。
15.【答案】AC
【解析】
【分析】
根据竖直上抛运动的对称性,结合自由落体运动列式求解即可。
本题考查了竖直上抛运动,根据竖直上抛运动的特点,结合自由落体运动列式求解。
【解答】
AB.第一次碰撞到第二次碰撞用时2s,根据竖直上抛运动的对称性知,上升时间为1s,则由速度公式得碰撞后的速度为:,故A正确,B错误;
C.第二次碰撞到第三次碰撞用时1s,根据竖直上抛运动的对称性知,上升时间为0.5s,下落时间也为0.5s,则上升高度为:,故C正确;
D.根据图像知,从第二次碰撞到第三次碰撞用时1s,而第三次弹起时,其速度减小,故在空中时间减小,故应在t=6s之前发生第四次碰撞,故D错误。
故选AC。
16.【答案】解:(1)选竖直向上的方向为正方向,,,在物块被人接住的前1s内位移x=4m,设被人接住的前1s的初速度为v1,在接住的前1s内由知:
(2)被人接住时物体的速度为:
所以物体从抛出到被人接住所经历的时间为:
(3)整个过程物块运动的位移就是二楼窗口距地面的高度:
【解析】本题考查了竖直上抛运动,竖直上抛运动是加速度为重力加速度的匀变速直线运动,运用匀变速直线运动的规律求解。
(1)通过位移时间公式求的接住前1s时的速度;
(2)根据速度时间公式求的时间;
(3)由位移速度公式求的位移。
17.【答案】解:
分成上升阶段和下落阶段两个过程处理.
绳子断裂后重物要继续上升的时间t1:
上升的高度h1:
故重物离地面的最大高度为:H=h1+h=180m
重物从最高处自由下落,落地时间:,由以上分析可知,重物落到地面用时:,
落地速度:v=gt2=60m/s。
【解析】由竖直上抛运动解得上升的时间,由自由落体运动解得下落时间,再解得总时间;由速度公式解得落地速度。
该题考查了竖直上抛运动的一般运用,把竖直上抛分成减速上升,和自由落体两个过程,可以简单求解。
18.【答案】解:当小球离电梯天花板最近时二者速度相同,即:
解得:
电梯发生位移:
小球发生位移:
小球离天花板最小距离:
方法二:以电梯为参考系小球初速度:
小球上升最大高度:
小球离天花板的最小距离:
以电梯为参考系
小球M位移:
小球m位移:
两小球相遇:
联立解得:
此时M相对地面速度:方向向上
m相对地面速度:方向向下???????
【解析】本题是力学的综合题,涉及知识较多,分析好物理情景,灵活应用公式是解决本题的关键。
(1)经分析,当小球离电梯天花板最近时二者速度相同,列式求出小球运动的时间,然后根据位移公式求小球离天花板的最小距离;
(2)以电梯为参考系,根据相遇时两球的位移关系求出相遇时间,然后根据速度公式求出两球相对地的速度。
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共40.0分)
做竖直上抛运动的物体( )
A.
在上升过程中,速度越来越小,加速度也越来越小
B.
在整个运动过程中,加速度大小不变方向改变
C.
上升和下降经过同一位置速度相同
D.
上升和下降经过同一段高度的过程中,上升时间等于下降时间
建筑工人常常徒手抛砖块,当砖块上升到最高点时被楼上的师傅接住用以砌墙.如所示,若某次以10
m/s的速度从地面竖直向上抛出一个砖块,g取10
m/s2,空气阻力可以忽略,则?
(???
)
A.
砖块上升的最大高度为10
m
B.
砖块上升的时间为1
s
C.
抛出后经0.5
s上升的高度为最大高度的一半
D.
抛出后上升过程砖块做加速度变化的减速直线运动
将一小球从足够高的塔顶以某初速度竖直向上抛出,经时间t=2s小球的速度大小为v=5m/s,忽略空气阻力,重力加速度g=10m/s2.则下列说法正确的是( )
A.
初速度大小一定为15m/s,2s末小球在抛出点上方10m处
B.
初速度大小一定为15m/s,2s末小球在拋出点下方10m处
C.
初速度大小可能为25m/s,2s末小球在抛出点上方30m处
D.
初速度大小可能为25m/s,2s末小球在抛出点下方30m处
将质量为m的小球甲和质量为2m的小球乙,分别从高地高度为h、2h处同时由静止释放,不计空气阻力和小球与地面碰撞的时间,碰撞后小球速度大小不变。则下列说法正确的是( )
A.
甲乙两球空中下落的加速度比之等于1:2
B.
甲乙第-次落地时速度大小之比等于1:2
C.
甲乙与地面第一次碰撞前下落的时间之比为1:2
D.
从开始下落计时时两球第一次在空中相遇
一个从地面竖直上抛的物体,它两次经过一个较低点a的时间间隔是Ta,两次经过一个较高点b的时间间隔是Tb,则a、b之间的距离为( )
A.
g(-)
B.
g(-)
C.
g(-)
D.
g(-)
一物体从某一行星表面竖直向上抛出(不计空气阻力),t=0时抛出,得到如图所示的x-t图象,则()
A.
该行星表面的重力加速度为10
m/s2
B.
该物体上升的时间为5
s
C.
该物体被抛出时的初速度为10
m/s
D.
该物体落到行星表面时的速度为20
m/s
每隔0.3s从同一高度抛出一个小球,小球做初速为6m/s的竖直上抛运动,设它们在空中不相碰.第一个小球在抛出点以上能遇到的小球数为(取g=10m/s2)( )
A.
三个
B.
四个
C.
五个
D.
六个
从地面上以初速度2υ0竖直上抛物体A,相隔时间△t后再以初速度υ0从同一地点竖直上抛物体B,不计空气阻力。以下说法正确的是(???
)
A.
物体A、B可能在物体A上升过程中相遇
B.
要使物体A、B相遇需要满足条件<△t<
C.
要使物体A、B相遇需要满足条件△t<
D.
要使物体A、B相遇需要满足条件△t>
一物体从地面以速度v竖直上抛,不计空气阻力,经过t时间到最高点,上升高度为h,则()
A.
物体通过前半程和后半程所用时间之比为1:(-1)
B.
物体通过h/2处的速度为v/2
C.
物体经过t/2时的速度为v/2
D.
物体经过前t/2和后t/2的位移之比为1:3
一个人在离地某高度处以相同的速率V0抛出两个物体A、B,A被竖直上抛,B被竖直下抛,这两个物体落地时间相差是△t,则初速度V0的大小为( )
A.
g△t
B.
g△t
C.
g△t
D.
g△t
二、多选题(本大题共5小题,共20.0分)
将一物体以的初速度竖直上拋,不计空气阻力,g取,则在第1s内物体的(????)
A.
位移大小为
B.
路程为
C.
平均速度的大小为
D.
速度改变量的大小为
如图所示,两端点分别为A、B,长L=1m的金属细杆在距地面H=40m处以v0=10m/s竖直上抛,同时在AB上方略微错开的竖直线上h处有一可视为质点的小球C由静止释放,不计空气阻力及落地后的运动,取g=10
m/s2,则可知
A.
杆从抛出到落地共用时4
s
B.
杆能上升的最大位移为10
m
C.
若h=15
m,则C与A相遇时杆的速度方向向下,与杆相遇共用时0.1
s
D.
若h=25
m,则C与A相遇时杆的速度方向向下,与杆相遇共用时0.1
s
(多选)在塔顶边缘将一物体竖直向上抛出,抛出点为A,物体上升的最大高度为20
m,不计空气阻力,g=10
m/s2,设塔足够高,则物体位移大小为10
m时,物体运动的时间可能为(
)
A.
(2-)s
B.
(2+)s
C.
(2+)s
D.
s
(多选)在地面上某处将一金属小球竖直向上抛出,上升一定高度后再落回原处。若不考虑空气阻力,则如图所示图像能正确反映小球的速度v、加速度a、位移x和速率v随时间变化关系的是(取向上为正方向)(
)
A.
B.
C.
D.
一小球自t=0时刻从水平地面上方某处自由下落,小球与地面碰后反向弹回,不计空气阻力,也不计小球与地面碰撞的时间间隔,小球距地面的高度h与运动时间t关系如图所示,取g=10m/s2.则(
)
A.
小球第一次与地面碰撞后的最大速度为10m/s
B.
小球第一次与地面碰撞后的最大速度为20m/s
C.
小球第二次与地面碰撞后上升的最大高度为1.25m
D.
小球将在t=6s时与地面发生第四次碰撞
三、计算题(本大题共3小题,共30.0分)
在一楼,有人将一物块以12
m/s的速度竖直向上抛出,物块冲过二楼窗口时被人接住,在被人接住前1
s内物块的位移是4
m,且位移方向向上,不计空气阻力,g取10
m/s2,求:
(1)人接住物块前1
s时物块的速度v
(2)物块从抛出到被人接住所经历的时间;
(3)二楼窗口距地面的高度.
气球下挂一重物,以v0=10
m/s的速度匀速上升,当到达离地高度h=175
m处时,悬挂重物的绳子突然断裂,那么重物经多长时间落到地面?落地时的速度?空气阻力不计,g取10
m/s2。
如图,某游乐场有高为的电梯以匀速上升,电梯内部离底面高处有一发射器.某时刻发射器向上发射一个速度、质量的小球.重力加速度.
求小球离天花板的最小距离;
如果发射小球M的同时,在小球正上方的天花板顶部以的速度向下发射一个质量的小球,两个小球发生正碰,求碰撞前各自的速度
答案和解析
1.【答案】D
【解析】解:A、做竖直上抛运动的物体,上升过程中速度向上,加速向下,速度减小,但加速度不变,故A错误;
B、整个运动过程中物体只受重力,加速度大小方向都不变,故B错误;
C、由对称性可知,物体回到抛出点时的速度大小不变,但方向相反,故C错误;
D、由对称性可知,向上和向下为互逆过程,上升和下降经过同一段高度的过程中时间相等,故D正确;
故选:D。
物体上升是匀减速运动,整个过程只受重力,加速度不变;由竖直上抛的对称性可知回到抛出点的速度和时间;
本题考查竖直上抛运动的规律,注意竖直上抛运动可分为向上运动和向下运动两段进行分析,而向上和向下为互逆过程,即向上的匀减速运动可看作向下的匀加速运动。
2.【答案】B
【解析】A.砖块做竖直上抛运动,上升的最大高度为,故A错误;
B.砖块上升的时间为,故B正确;
???????CD.砖块上升过程做匀减速直线运动,速度不断减小,所以前0.5s内上升的高度大于后0.5s上升的高度,则抛出后经0.5s上升的高度大于最大高度的一半,故CD错误。
故选B。
砖块做竖直上抛运动,可以看作加速度为-g的匀减速直线运动,由速度位移公式求最大高度.由速度时间公式即可求得上升的时间。
本题考查了竖直上抛运动;竖直上抛运动是常见的运动,是高考的热点,将竖直上抛运动看成一种匀减速直线运动,采用分段法研究比较好理解。
3.【答案】C
【解析】解:经时间t=2s小球的速度大小为v=5m/s,速度方向可能向上也可能向下;取向上为正;
当t=2s小球的速度为v=5m/s,则初速度v=v0-gt可得:v0=25m/s,此时小球在在抛出点上方h==m=30m处;
当t=2s小球的速度为v=-5m/s,则初速度v=v0-gt可得:v0=15m/s,此时小球在在抛出点上方h==m=10m处。故C正确、ABD错误。
故选:C。
当t=2s小球的速度为v=5m/s或速度为v=-5m/s时,求出初速度大小,再根据位移关系求解。
本题主要是考查竖直上抛运动,解答本题的关键是知道速度是一个矢量,末速度大小为5m/s,方向可能向上、可能向下。
4.【答案】D
【解析】解:A、不计空气阻力,自由落体运动的加速度与质量无关,故A错误;
B、落地速度等于v2=2gh,,高度之比等于1:2,落地时速度之比等于,故B错误;
C、下落高度与时间的关系是,显然时间之比也等于,故C错误;
D、甲球先落地,速度大小为v,此时乙球速度也为v,乙球也下落了h,设再过一段时间△t,二者在空中相遇,则有:,而甲球下落h的时间为故第一次相遇的时刻为,故D正确。
故选:D。
两小球均做自由落体运动,根据自由落体运动规律可确定加速度、速度以及时间关系;再分析两球的运动过程,根据运动学公式确定相遇时间。
本题考查自由落体运动以及竖直上抛运动规律,要注意两球在空中均做自由落体运动;但由于下落高度不同,故距离h的小球落地反弹后与球乙相遇。
5.【答案】B
【解析】解:小球做竖直上抛运动,根据运动时间的对称性得,物体从最高点自由下落到A点的时间为,物体从最高点自由下落到B点的时间为,
竖直上抛运动的加速度a=g,由x=at2可得:
最高点到A点的距离为:xA=gTa2…①
最高点到B点的距离为:xB=gTb2…②
A点在B点下方,由①、②解得,AB相距为:
△x=g(Ta2-Tb2)。
故选:B。
因为是上抛运动可以利用对称来解,可以得到物体从顶点到a的时间为,顶点到B点的时间为,
从顶点出发初速度为0,经过t时间到达某个点,位移式x=at2将其带入求解.
竖直上抛上去和下来具有对称性,所需的时间是一样的,所以只要讨论下来就可以,在最高点速度是0,就是个初速度为0的匀加速运动.
6.【答案】D
【解析】
【分析】
物体从行星表面竖直上抛,由图读出最大高度和上升的时间,根据运动学公式求出初速度和重力加速度。物体落回行星表面的速度与抛出时速度大小相等。
本题首先考查读图能力,图上能读出最大高度、上升和下落时间等等;其次要灵活选择运动学公式求解。
【解答】
ABC.由图读出,物体上升的最大高度为h=25m,上升的时间为t=2.5s,
对于上升过程,有h=得,初速度v0==m/s=20m/s,
物体上升的加速度大小a=g==m/s2=8m/s2,故ABC错误;
D.根据对称性可知,该物体落到行星表面时的速度大小与初速度大小相等,也为20m/s,故D正确。
故选D。
7.【答案】A
【解析】解:小球做竖直上抛运动,从抛出到落地的整个过程是匀变速运动,根据位移时间关系公式,有:
x=v0t-gt2
代入数据,有:
0=6t-×10×t2
解得:t=0(舍去)或
t=1.2s
每隔0.3s抛出一个小球,故第一个小球在抛出点以上能遇到的小球数为:
N=-1=3
故选:A。
小球做竖直上抛运动,先求解出小球运动的总时间,然后判断小球在抛出点以上能遇到的小球数.
本题关键明确第一个小球的运动情况,然后选择恰当的运动学公式列式求解出运动时间,再判断相遇的小球个数.
8.【答案】B
【解析】
【分析】
两个物体空中都做竖直上抛运动,相遇可能有几种情况:①A、B均在下降,A追上B;②A在下降,B在上升。根据运动学规律求出两物体在空中运动的总时间,两物体抛出的时间间隔Δt必须满足条件:①抛出B时A不能已经落地;②B不能先落地,即A在B前落.由此分析间隔Δt必须满足条件。
本题关键要判断出物体A、B只能在物体A下降过程中相遇,根据两球运动的总时间关系,分析抛出时的时间间隔。
【解答】
A.A物体上升时,A的初速度大于B的初速度,且A先抛出,所以A的位移大于B的位移,不可能在A上升的过程中相遇,故A错误;
BCD.A在空中的总时间为t1=2×=;B在空中的总时间为t2=,要使A、B能在空中相遇,t1-t2<Δt<t1,即得:<Δt<,故B正确,CD错误。
故选B。
9.【答案】C
【解析】
【分析】
物体做竖直上抛运动,其逆运动为自由落体运动,初速度为零;由匀变速直线运动的规律进行分析解答。
本题考查自由落体的运动规律,要注意明确自由落体就是初速度为零,加速度为g的匀加速直线运动;所有运动学公式及结论均可以使用。
【解答】
解:A、设全程高度为h,则由位移公式可知,h=gt2;则前半程的时间t1=;全程的时间t=;则后半程所用时间为t2=t-t1=;因本题为上抛运动,为自由落体的逆运动,故前后半程内的时间之比为:():1;故A错误;
B、由v2=2gh可得,通过时的速度为,落地时的速度为:,故,故B错误;
C、由v=gt可得,物体通过时的速度v=g=,故C正确;
D、做自由落体运动时,前一半时间内的平均速度为;而后一半时间内的平均速度为;本题为竖直上抛运动,故前后一半时间内的速度之比为3:1;故D错误;
故选C。
10.【答案】B
【解析】解:根据机械能守恒可知两个物体落地时的速度大小相等,设为v。
对于竖直上抛,取竖直向上为正方向,则有t1==
对于竖直下抛,有t2=
据题△t=t1-t2=
则v0=g△t
故选:B。
竖直下抛是匀加速直线运动,竖直上抛是匀减速直线运动,根据速度位移公式分别列式两个运动的时间,即可求解。
本题关键要熟练运用运动学速度时间公式列出时间表达式,要注意取竖直向上为正方向时,竖直上抛运动的加速度为-g,落地时速度大小为-v。
11.【答案】BCD
【解析】
【分析】
物体竖直上抛后,只受重力,加速度等于重力加速度,可以把物体的运动看成一种匀减速直线运动,由位移公式求出1s内位移,由平均速度公式求出平均速度,由△v=at求出速度的改变量。对于竖直上抛运动,通常有两种处理方法,一种是分段法,一种是整体法,两种方法可以交叉运用。
【解答】
?A、1s内物体的位移为:x=m=3m,方向竖直向上,故A错误;
B、物体上升的最大位移为:m,物体上升和下落的总路程为3.2m+(3.2-3.0)m=3.4m,所以1s内的路程是3.4m,故B正确;
C、平均速度:=m/s.故C正确;
D、速度改变量的大小为:△v=at=gt=10×1m/s=10m/s。故D正确。
故选:BCD
12.【答案】ACD
【解析】略
13.【答案】ABC
【解析】[解析] 物体在塔顶边缘的A点抛出,位移大小为10
m的位置有两处,如图所示,一处在A点之上,另一处在A点之下,在A点之上时,通过位移大小为10
m处有上升和下降两种过程,在A点之下10
m处只有下降过程。
法一:分段法
由H=,得v0=20
m/s,
物体上升10
m时,速度为v1,则由v12-v02=-2gh,
得v1=10?m/s,
则t1==(2-)s,故A对;
物体从抛出到下落至A点上方10
m时,
t2=t1+=(2+)s,故B对;
物体从最高点到下落至A点下方10
m处时,
H+h=gt32,则t3=?s,
故物体从抛出到下落至A点下方10
m处时,
t3′=+t3=(2+)s,故C对,D错。
法二:全程法
取竖直向上为正方向,物体的位移为x=v0t-gt2,
当物体位于A点上方10
m处时x=10
m,
解得t1=(2-)s,t2=(2+)s,故选项A、B对。
当物体位于A点下方10
m处时,x=-10
m,
解得t3=(2+)s,另一解为负值,舍去,故选项C对,D错。
[答案]ABC
14.【答案】AD
【解析】金属小球做竖直上抛运动,上升和下降过程加速度大小和方向都不变,做匀变速直线运动,速度图像应是倾斜的直线。以向上为正方向,速度先正后负,加速度为负值,A正确,B错误;上升过程速率均匀减小,下降过程速率均匀增加,D正确;根据位移时间关系式:x=v0t+at2可知位移时间图像是抛物线,C错误。故选AD。
15.【答案】AC
【解析】
【分析】
根据竖直上抛运动的对称性,结合自由落体运动列式求解即可。
本题考查了竖直上抛运动,根据竖直上抛运动的特点,结合自由落体运动列式求解。
【解答】
AB.第一次碰撞到第二次碰撞用时2s,根据竖直上抛运动的对称性知,上升时间为1s,则由速度公式得碰撞后的速度为:,故A正确,B错误;
C.第二次碰撞到第三次碰撞用时1s,根据竖直上抛运动的对称性知,上升时间为0.5s,下落时间也为0.5s,则上升高度为:,故C正确;
D.根据图像知,从第二次碰撞到第三次碰撞用时1s,而第三次弹起时,其速度减小,故在空中时间减小,故应在t=6s之前发生第四次碰撞,故D错误。
故选AC。
16.【答案】解:(1)选竖直向上的方向为正方向,,,在物块被人接住的前1s内位移x=4m,设被人接住的前1s的初速度为v1,在接住的前1s内由知:
(2)被人接住时物体的速度为:
所以物体从抛出到被人接住所经历的时间为:
(3)整个过程物块运动的位移就是二楼窗口距地面的高度:
【解析】本题考查了竖直上抛运动,竖直上抛运动是加速度为重力加速度的匀变速直线运动,运用匀变速直线运动的规律求解。
(1)通过位移时间公式求的接住前1s时的速度;
(2)根据速度时间公式求的时间;
(3)由位移速度公式求的位移。
17.【答案】解:
分成上升阶段和下落阶段两个过程处理.
绳子断裂后重物要继续上升的时间t1:
上升的高度h1:
故重物离地面的最大高度为:H=h1+h=180m
重物从最高处自由下落,落地时间:,由以上分析可知,重物落到地面用时:,
落地速度:v=gt2=60m/s。
【解析】由竖直上抛运动解得上升的时间,由自由落体运动解得下落时间,再解得总时间;由速度公式解得落地速度。
该题考查了竖直上抛运动的一般运用,把竖直上抛分成减速上升,和自由落体两个过程,可以简单求解。
18.【答案】解:当小球离电梯天花板最近时二者速度相同,即:
解得:
电梯发生位移:
小球发生位移:
小球离天花板最小距离:
方法二:以电梯为参考系小球初速度:
小球上升最大高度:
小球离天花板的最小距离:
以电梯为参考系
小球M位移:
小球m位移:
两小球相遇:
联立解得:
此时M相对地面速度:方向向上
m相对地面速度:方向向下???????
【解析】本题是力学的综合题,涉及知识较多,分析好物理情景,灵活应用公式是解决本题的关键。
(1)经分析,当小球离电梯天花板最近时二者速度相同,列式求出小球运动的时间,然后根据位移公式求小球离天花板的最小距离;
(2)以电梯为参考系,根据相遇时两球的位移关系求出相遇时间,然后根据速度公式求出两球相对地的速度。
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
