图形的旋转第1课时

(共14张PPT)
刮水器
转动的车轮
转动的时针
荡秋千
这些运动有什么共同的特征？
B
A
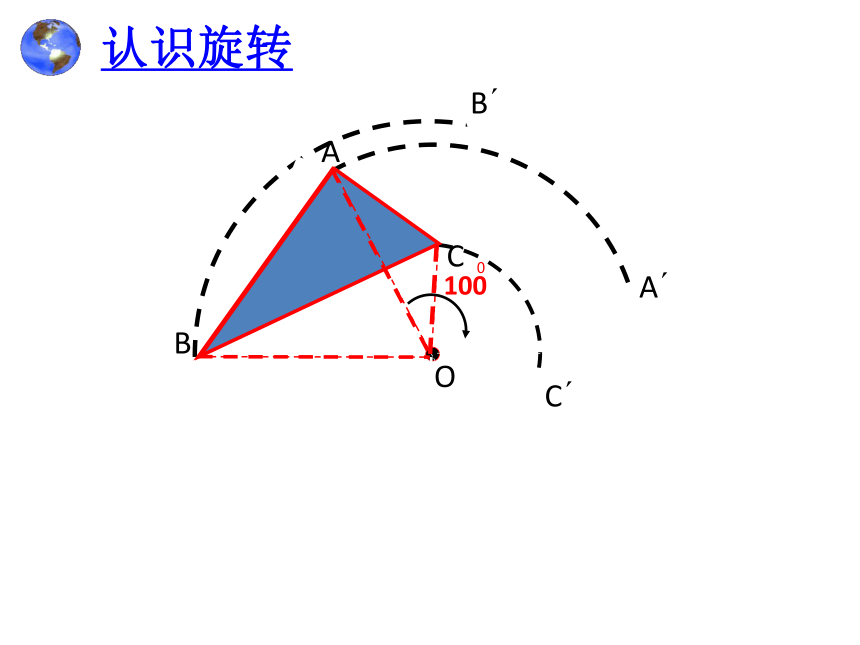
认识旋转
B
A
C
C
O
100
0
O
B
A
B
/
A
/
B
A
B
A
C
C
O
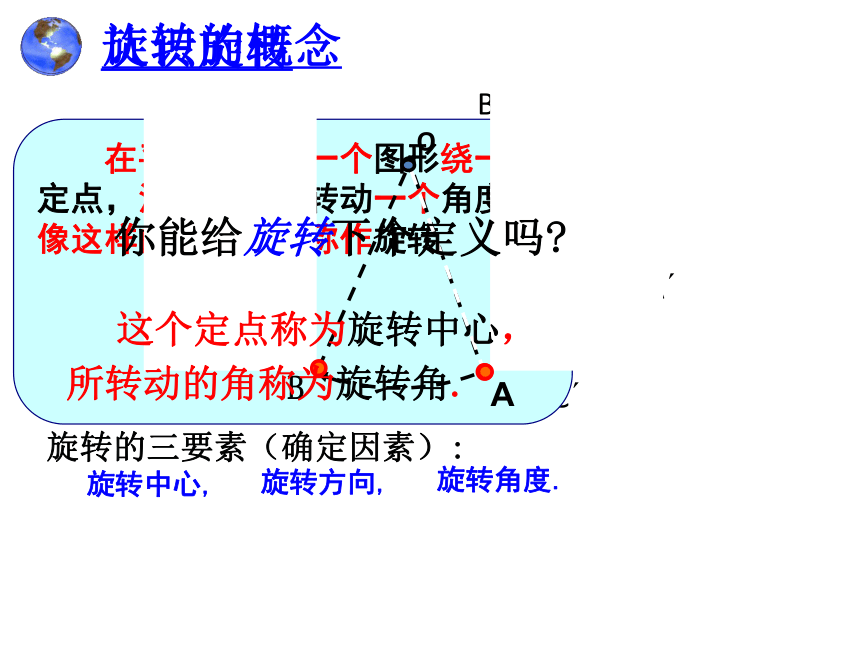
在平面内，把一个图形绕一个定点，沿某个方向转动一个角度，像这样的图形变换称作旋转
B
O
A
认识旋转
这个定点称为旋转中心，
旋转的概念
旋转的三要素（确定因素）:
旋转中心,
旋转方向,
旋转角度.
所转动的角称为旋转角.
你能给旋转下个定义吗
B
A
B
A
C
C
O
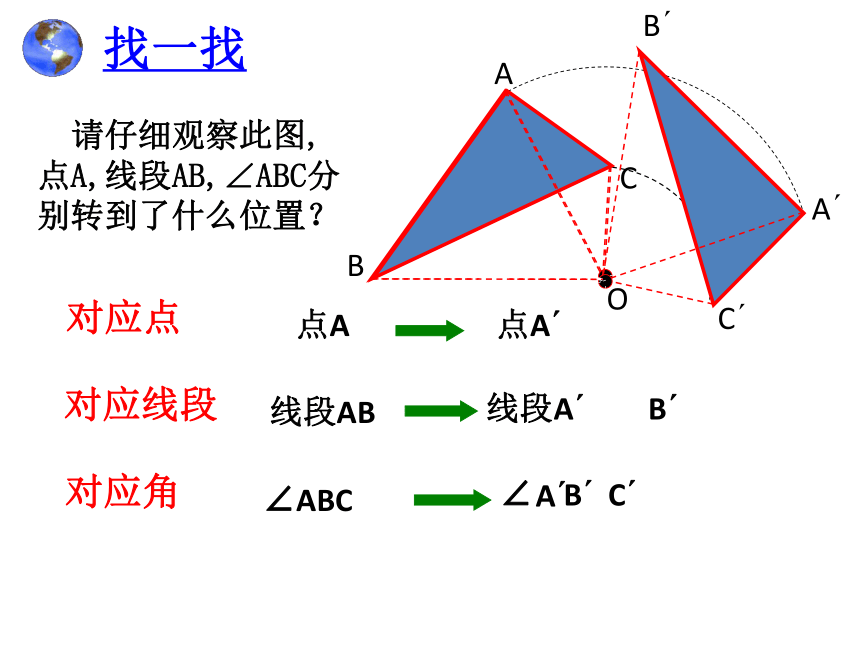
找一找
请仔细观察此图,
点A,线段AB,∠ABC分
别转到了什么位置？
点A
点A
线段A
B
∠ B
A
C
线段AB
∠ABC
对应点
对应线段
对应角
试一试
A
B
O
C
D
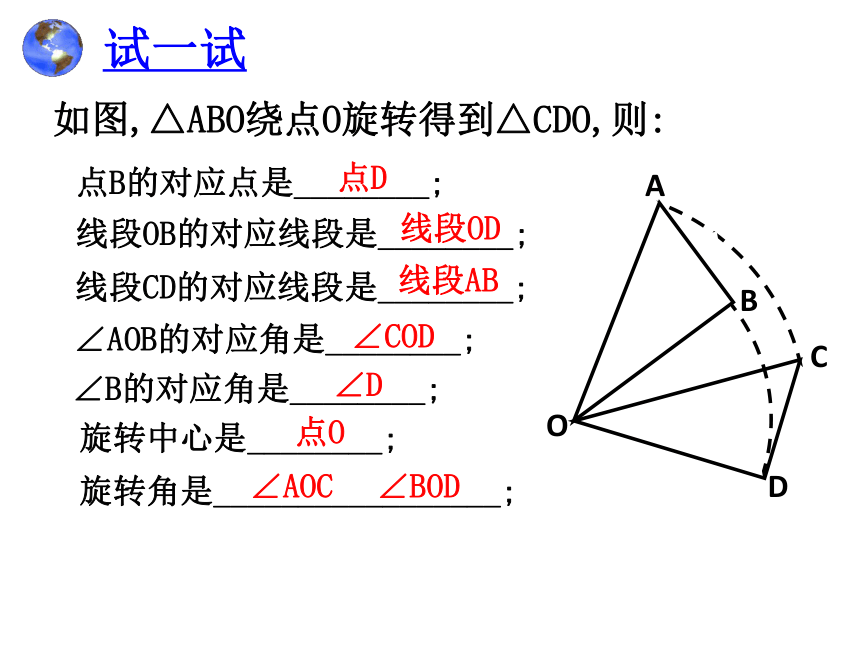
点B的对应点是________;
线段OB的对应线段是________;
线段CD的对应线段是________;
∠AOB的对应角是________;
∠B的对应角是________;
旋转中心是________;
旋转角是_________________;
如图,△ABO绕点O旋转得到△CDO,则:
点D
线段OD
线段AB
∠COD
∠D
点O
∠AOC
∠BOD
D
E
A
B
F
C
O
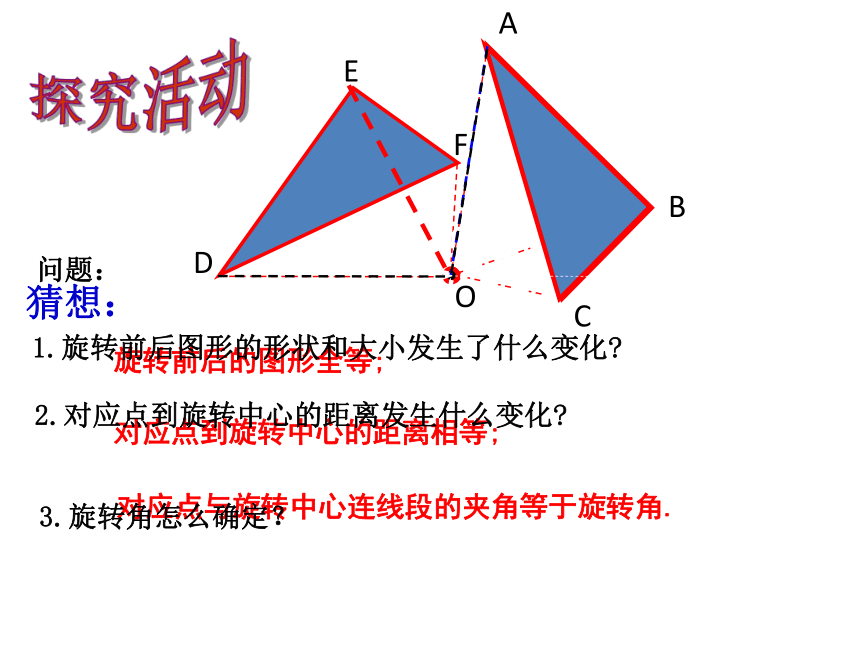
问题：
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心连线段的夹角等于旋转角.
猜想：
1.旋转前后图形的形状和大小发生了什么变化
2.对应点到旋转中心的距离发生什么变化
3.旋转角怎么确定？
旋转的基本性质
◆旋转前、后的图形全等.
◆对应点到旋转中心的距离相等.
◆每一对对应点与旋转中心所连线段的夹角等于旋转角。
A
B
C
D
E
E′
如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.
分析：关键是确定△ADE三个顶点的对应点，即它们旋转后的位置.
例
3
44°
5
(第5题)
练习3.如图，△ABC为等边三角形，D是△ABC内一点，若将△ABD经过旋转后到△ACP位置，则旋转中心是__________，旋转角等于_________度，△ADP是___________三角形.已知AD=3,BD=4,CB=5则∠APC=______度.
一路下来，我们结识了很多
新知识，你能谈谈自己的收
获吗？说一说，让大家一起
来分享。
课堂回顾：这节课，主要学习了什么？
在平面内，将一个图形绕着一个定点沿某个方向转动一个角度，这样的图形运动称为旋转
旋转的概念：
旋转的性质：
1、旋转不改变图形的大小和形状．
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角，旋转角相等．
3、对应点到旋转中心的距离相等