直线与圆的位置关系（二）

(共15张PPT)
24.2.2 直线与圆的位置关系（二）
网市中学数学组
初中数学九年级上册
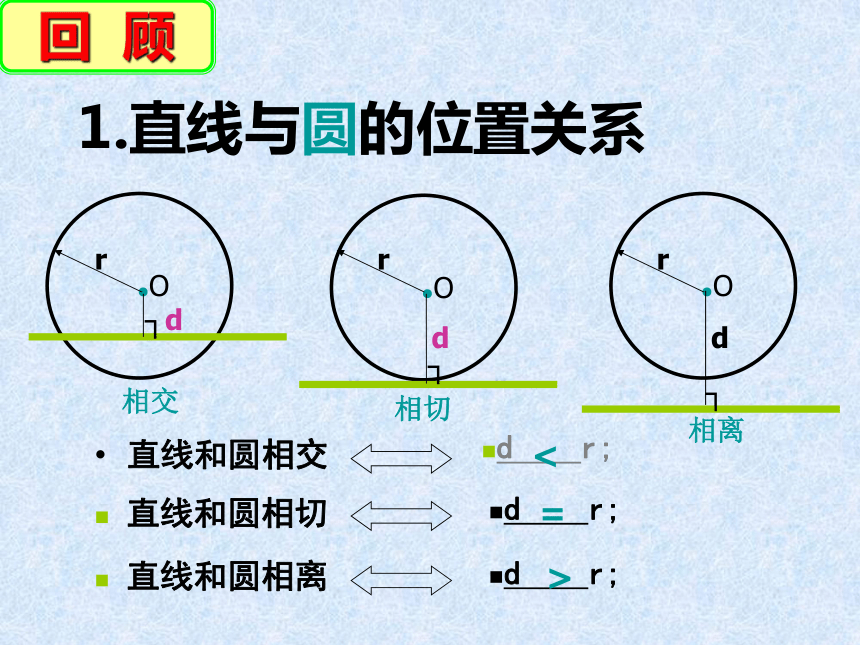
直线和圆相交
d r;
d r;
直线和圆相切
直线和圆相离
d r;
1.直线与圆的位置关系
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
回 顾
3.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
以点C为圆心, CM长为半径的圆与AB的
位置关系如何
2、问：怎样判定直线 与圆的位置关系
（1）根据定义，由__________________的个数来判断；
（2）根据性质，由_____________________ ______________的关系来判断。
直线 与圆的公共点
圆心到直线的距离d
与半径r
在实际应用中，常采用第二种方法判定。
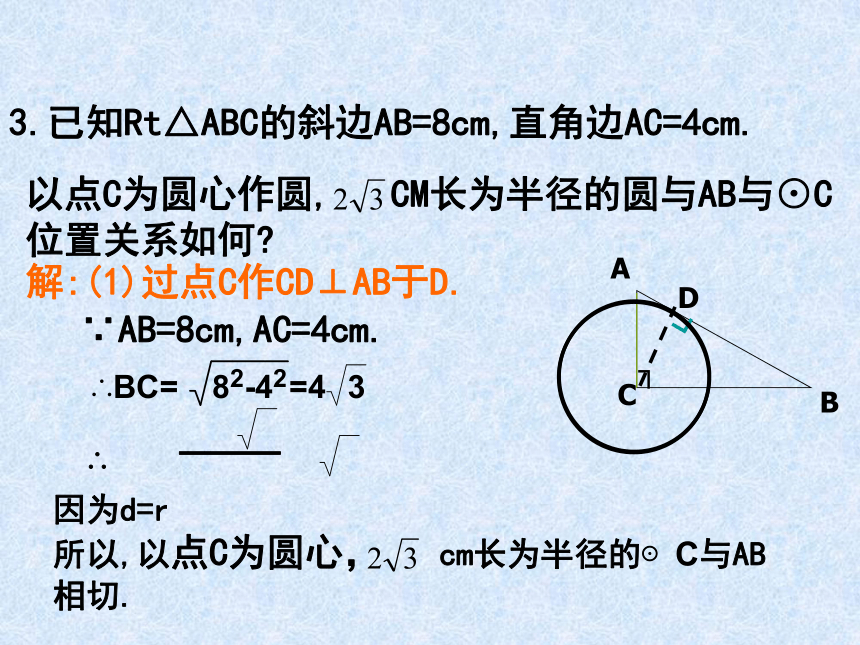
3.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
以点C为圆心作圆, CM长为半径的圆与AB与⊙C位置关系如何
A
C
B
┐
解:(1)过点C作CD⊥AB于D.
D
┛
∵AB=8cm,AC=4cm.
因为d=r
所以,以点C为圆心， cm长为半径的⊙C与AB相切.
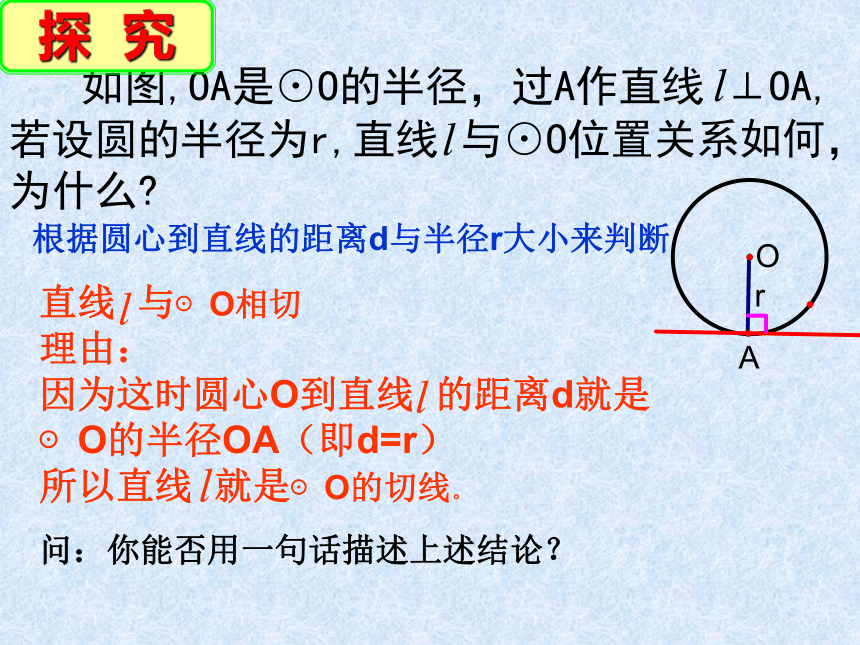
如图,OA是⊙O的半径，过A作直线 ⊥OA,若设圆的半径为r,直线 与⊙O位置关系如何，为什么
探 究
直线 与⊙O相切
理由：
因为这时圆心O到直线 的距离d就是⊙O的半径OA（即d=r）
所以直线 就是⊙O的切线。
问：你能否用一句话描述上述结论？
根据圆心到直线的距离d与半径r大小来判断
O
A
A
O
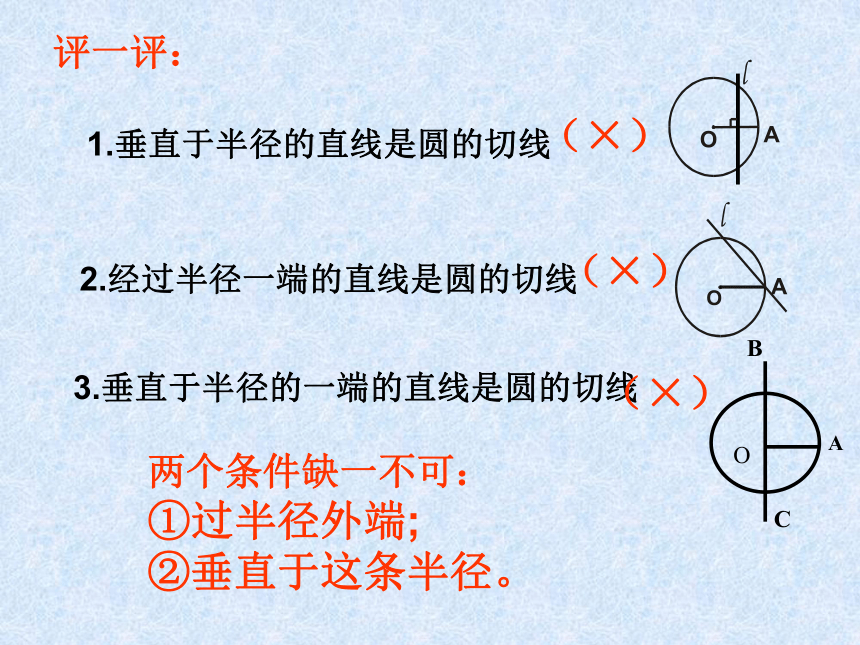
两个条件缺一不可：
①过半径外端;
②垂直于这条半径。
1.垂直于半径的直线是圆的切线
评一评：
2.经过半径一端的直线是圆的切线
（×）
（×）
3.垂直于半径的一端的直线是圆的切线
B
A
C
O
（×）
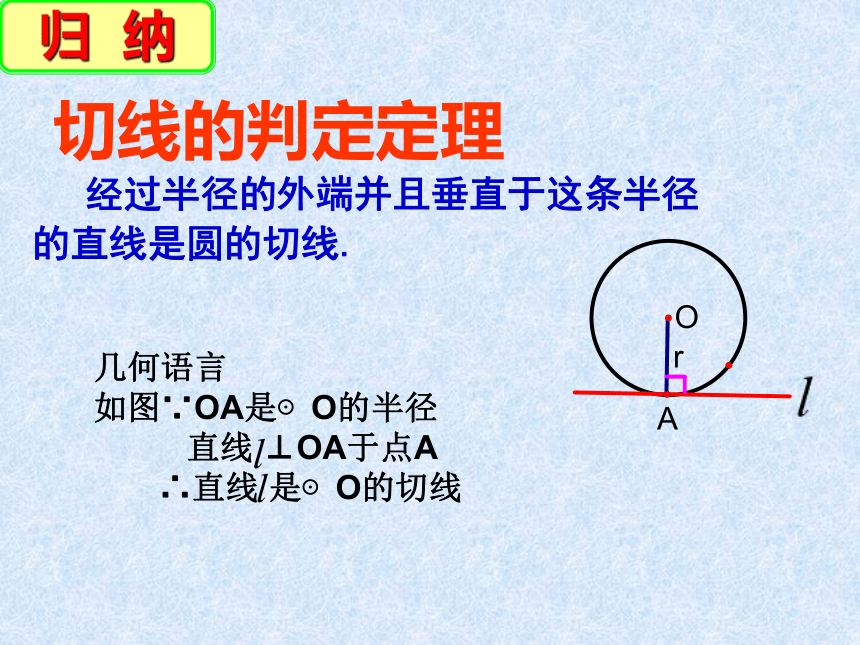
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的判定定理
归 纳
几何语言
如图∵OA是⊙O的半径
直线 ⊥OA于点A
∴直线 是⊙O的切线
例1.△ABC内接于⊙O，AB是⊙O的直径，∠1=∠B，判断直线AD与⊙O的位置关系，并说明理由.
典型例题
解：AD与⊙O相切
理由：
∵AB是⊙O的直径
∴∠ACB﹦90°
∴∠2＋∠B﹦ 90°
又∵ ∠1=∠B
∴∠1＋∠2﹦ 90°
即AD⊥AB
∴AD是⊙O的切线
归纳：判断一条直线是否是圆的切线，先看它是否经过半径的外端，然后判定它是否垂直这条半径。
　　变式 △ABC内接于⊙O，AB是⊙O的弦，∠CAD=∠ABC，判断直线AD与⊙O的位置关系，并说明理由.
E
2
证明一条直线是圆的切线时:
直线与圆有交点时，连接交点与圆心，证垂直.
即有点连半径，证垂直
解：连接AO并延长AO交⊙O于E，
连接EC
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
如图，AB与CD要么垂直，要么不垂直．假设AB与CD不垂直，过点O作一条直径垂直于CD、垂足为M，则OM＜OA，（垂线段最短）即圆心O到直线CD的距离小于⊙O的半径，因此CD与⊙O相交，这与已知条件“直线CD与⊙O相切”相矛盾，所以AB与CD垂直．
探索交流
D
A
B
C
O
N
M
（用反证法证明）
切线的性质定理
定理 圆的切线垂直于过切点的半径.
如图
∵CD是⊙O的切线,A是切点, ∴CD⊥OA.
D
C
●O
A
已知直线和圆相切时，
常用辅助线：
连接切点与圆心，得到垂直。
归 纳
例2.PA、PB是⊙O的切线，切点分别为A、B，C是⊙O上一点，若∠APB=40°，求∠ACB的度数.
典型例题
解：连接OA、OB
例3.点O是∠DPC的角平分线上的一点，⊙O与PD相切于A，
求证：PC与⊙O相切.
E
应用提升
证明：连接OA，
证一条线是圆的切线时常用辅助线：
有点连半径，证垂直；
无点作垂线，证半径。
∵ ⊙O与PD相切于A
∴OA⊥AD且OA为⊙O的半径
∵AO平分∠DPC
∴OE﹦OA
∴PC与⊙O相切
过点O作OE⊥PC于点E
证明一条直线是圆的切线时
（1）直线与圆有交点时，
连接交点与圆心，证垂直；
（2）直线与圆“无”交点时，
过圆心作直线的垂线，证明垂线段的长等于半径.
经过半径的外端并且垂直于这条半的直线是圆的切线.
1. 切线的判定定理
2.切线的性质定理
圆的切线垂直于过切点的半径.
总 结
课后训练
导学案：课后作业