九年级数学新人教版切线长定理(讲课用)
文档属性
| 名称 | 九年级数学新人教版切线长定理(讲课用) |  | |
| 格式 | rar | ||
| 文件大小 | 455.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-29 16:37:32 | ||
图片预览


文档简介
(共12张PPT)
网市中学初三数学组 2011.10.18
1、切线的判定定理:
2、切线的性质定理:
经过半径的外端且垂直于
这条半径的直线是圆的切线
圆的切线垂直于经过切点
的半径
复 习
4、思考:经过圆上一点可以作圆的几条切线?经过圆外一点呢?
3、判断直线与圆相切有几种方法?
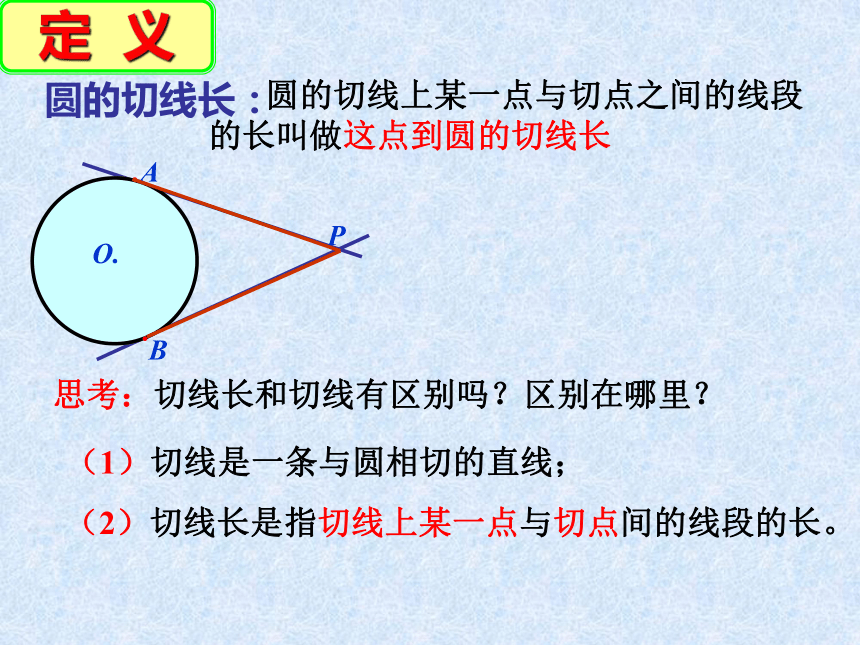
.A
B
P
O.
.
圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长
圆的切线长:
定 义
思考:切线长和切线有区别吗?区别在哪里?
(1)切线是一条与圆相切的直线;
(2)切线长是指切线上某一点与切点间的线段的长。
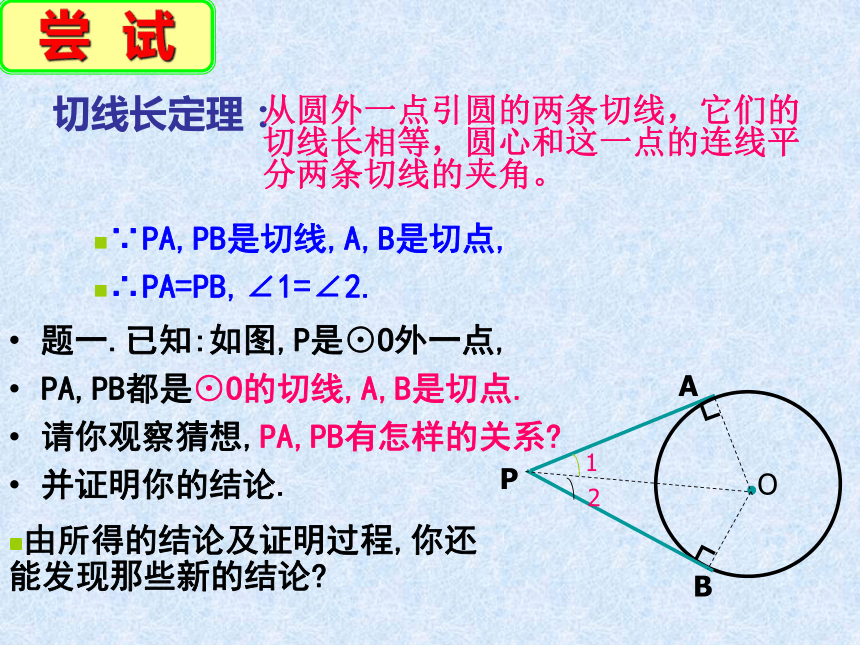
题一.已知:如图,P是⊙O外一点,
PA,PB都是⊙O的切线,A,B是切点.
请你观察猜想,PA,PB有怎样的关系
并证明你的结论.
由所得的结论及证明过程,你还能发现那些新的结论
尝 试
A
B
P
●O
┗
┏
1
2
切线长定理:
从圆外一点引圆的两条切线,它们的
切线长相等,圆心和这一点的连线平
分两条切线的夹角。
∵PA,PB是切线,A,B是切点,
∴PA=PB,∠1=∠2.
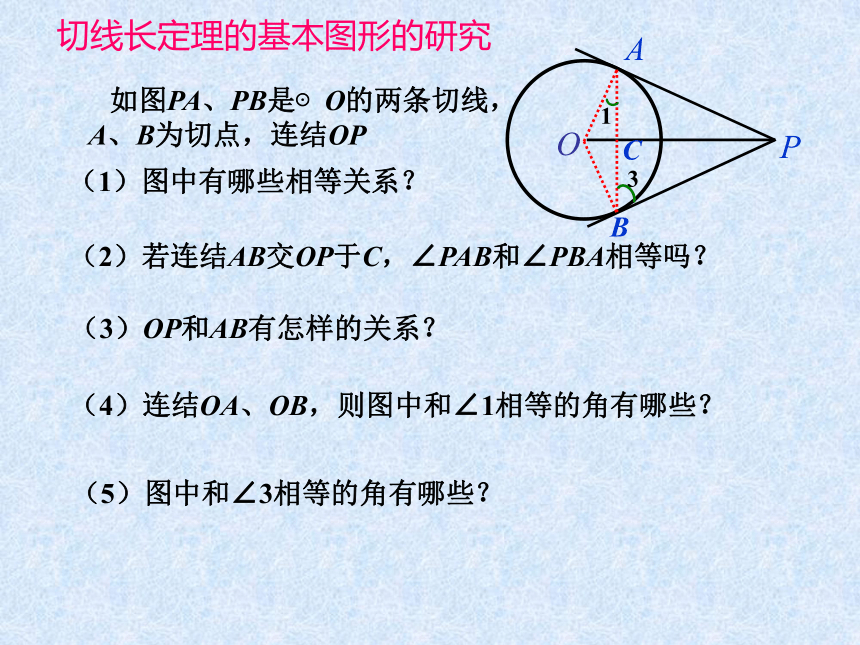
如图PA、PB是⊙O的两条切线,
A、B为切点,连结OP
B
A
P
O
切线长定理的基本图形的研究
(1)图中有哪些相等关系?
C
(2)若连结AB交OP于C,∠PAB和∠PBA相等吗?
(3)OP和AB有怎样的关系?
1
(4)连结OA、OB,则图中和∠1相等的角有哪些?
3
(5)图中和∠3相等的角有哪些?
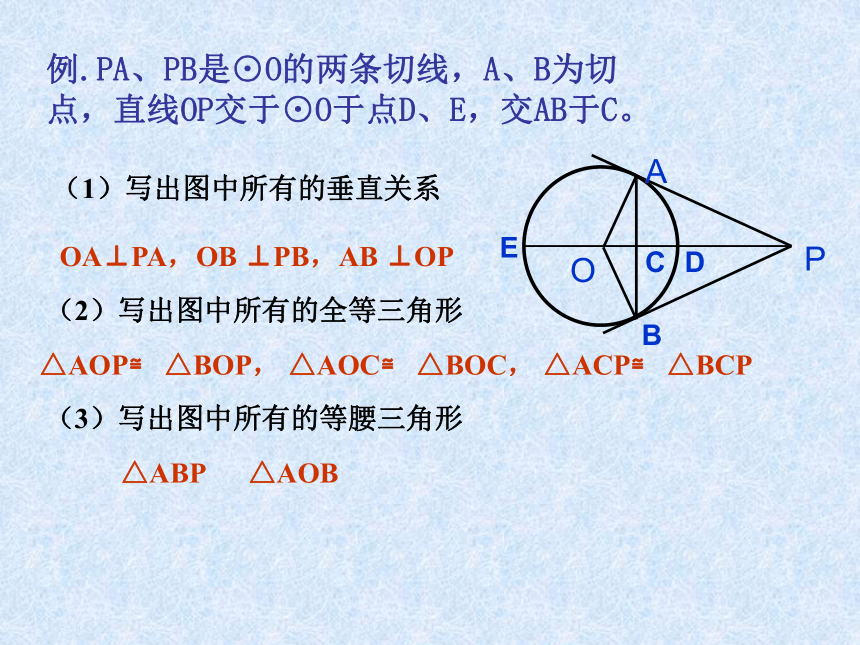
例.PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(2)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(3)写出图中所有的等腰三角形
△ABP △AOB
例1:(1)如图,已知⊙O的半径为3cm,点P和圆心O的距离为 6cm,经过点P有⊙O的两条切线PA、PB,则切线长为_____cm,这两条切线的夹角为____
A
B
P
.
O.
,∠AOB=______
典型例题
P
(2)如图,从⊙O外一点P作⊙O的两条切线,分别切⊙O于A,B,在AB 上任取一点C作⊙O的切线分别交PA、PB于D、E
B
.
D
C
E
O
A
.
.
若PA=2,则△PDE的周长为______;
若PA=a,则△PDE
的周长为_______
例2:
数学课上,数学老师把一个乒乓球放在一个V形架中,如图是它的平面示意图,CA、CB是⊙O的切线,切点分别是A、B,某同学通过测量,量得AB=4cm,∠ACB=600,如何求出乒乓球的直径?
.
.
O
C
A
B
D
典型例题
解:连接OB、OC交AB于D
求证:PO⊥OQ
1.如图AB是⊙O的直径,C为圆上任意一点,过C的切线分别与过A、B两点的切线交于P、Q,
O
.
A
B
C
P
Q
∴PO⊥OQ
1
2
由AB为直径可得AP//BQ
由PA、PQ、BQ为切线
分析:
可得
练 习
∠1= ∠APC
∠2= ∠BQC
则有∠1+∠2=90°
1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
总结:
A
P
O
。
B
E
C
D
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
OP垂直平分AB
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。
反思:在解决有关圆的切线长问题时,往往 需要我们构建基本图形。
(1)分别连结圆心和切点
(2)连结两切点
(3)连结圆心和圆外一点
作 业
1.把一个乒乓球放在一个V形架中,如图是它的平面示意图,CA、CB是⊙O的切线,切点分别是A、B,某同学通过测量,量得AB=4cm,∠ACB=600,如何求出乒乓球的直径?
.
.
O
C
A
B
D
2.课本P103 第12题
网市中学初三数学组 2011.10.18
1、切线的判定定理:
2、切线的性质定理:
经过半径的外端且垂直于
这条半径的直线是圆的切线
圆的切线垂直于经过切点
的半径
复 习
4、思考:经过圆上一点可以作圆的几条切线?经过圆外一点呢?
3、判断直线与圆相切有几种方法?
.A
B
P
O.
.
圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长
圆的切线长:
定 义
思考:切线长和切线有区别吗?区别在哪里?
(1)切线是一条与圆相切的直线;
(2)切线长是指切线上某一点与切点间的线段的长。
题一.已知:如图,P是⊙O外一点,
PA,PB都是⊙O的切线,A,B是切点.
请你观察猜想,PA,PB有怎样的关系
并证明你的结论.
由所得的结论及证明过程,你还能发现那些新的结论
尝 试
A
B
P
●O
┗
┏
1
2
切线长定理:
从圆外一点引圆的两条切线,它们的
切线长相等,圆心和这一点的连线平
分两条切线的夹角。
∵PA,PB是切线,A,B是切点,
∴PA=PB,∠1=∠2.
如图PA、PB是⊙O的两条切线,
A、B为切点,连结OP
B
A
P
O
切线长定理的基本图形的研究
(1)图中有哪些相等关系?
C
(2)若连结AB交OP于C,∠PAB和∠PBA相等吗?
(3)OP和AB有怎样的关系?
1
(4)连结OA、OB,则图中和∠1相等的角有哪些?
3
(5)图中和∠3相等的角有哪些?
例.PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(2)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(3)写出图中所有的等腰三角形
△ABP △AOB
例1:(1)如图,已知⊙O的半径为3cm,点P和圆心O的距离为 6cm,经过点P有⊙O的两条切线PA、PB,则切线长为_____cm,这两条切线的夹角为____
A
B
P
.
O.
,∠AOB=______
典型例题
P
(2)如图,从⊙O外一点P作⊙O的两条切线,分别切⊙O于A,B,在AB 上任取一点C作⊙O的切线分别交PA、PB于D、E
B
.
D
C
E
O
A
.
.
若PA=2,则△PDE的周长为______;
若PA=a,则△PDE
的周长为_______
例2:
数学课上,数学老师把一个乒乓球放在一个V形架中,如图是它的平面示意图,CA、CB是⊙O的切线,切点分别是A、B,某同学通过测量,量得AB=4cm,∠ACB=600,如何求出乒乓球的直径?
.
.
O
C
A
B
D
典型例题
解:连接OB、OC交AB于D
求证:PO⊥OQ
1.如图AB是⊙O的直径,C为圆上任意一点,过C的切线分别与过A、B两点的切线交于P、Q,
O
.
A
B
C
P
Q
∴PO⊥OQ
1
2
由AB为直径可得AP//BQ
由PA、PQ、BQ为切线
分析:
可得
练 习
∠1= ∠APC
∠2= ∠BQC
则有∠1+∠2=90°
1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
总结:
A
P
O
。
B
E
C
D
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
OP垂直平分AB
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。
反思:在解决有关圆的切线长问题时,往往 需要我们构建基本图形。
(1)分别连结圆心和切点
(2)连结两切点
(3)连结圆心和圆外一点
作 业
1.把一个乒乓球放在一个V形架中,如图是它的平面示意图,CA、CB是⊙O的切线,切点分别是A、B,某同学通过测量,量得AB=4cm,∠ACB=600,如何求出乒乓球的直径?
.
.
O
C
A
B
D
2.课本P103 第12题
同课章节目录
