5.2.1 三角函数的概念 同步课件(共26张PPT)
文档属性
| 名称 | 5.2.1 三角函数的概念 同步课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 277.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 13:59:39 | ||
图片预览







文档简介
第五章 三角函数
5.2.1 三角函数的概念
教学目标
1.借助单位圆理解任意角三角函数的定义;
2.根据定义认识函数值的符号,理解诱导公式一;
3.能初步运用定义分析和解决与三角函数值有关的一些简单问题;
4.体验三角函数概念的产生、发展过程,领悟直角坐标系的工具功能,丰富数形结合的经验。
重点难点
重点:
任意角的三角函数(正弦函数、余弦函数、正切函数)的定义;
难点:
任意角的三角函数概念的建构过程。
温故知新
知识点一 任意角
1、角的概念
角可以看成平面内一条 射线 绕着端点从一个位置 旋转 到另一个位置所成的 图形 .
温故知新
知识点一 任意角
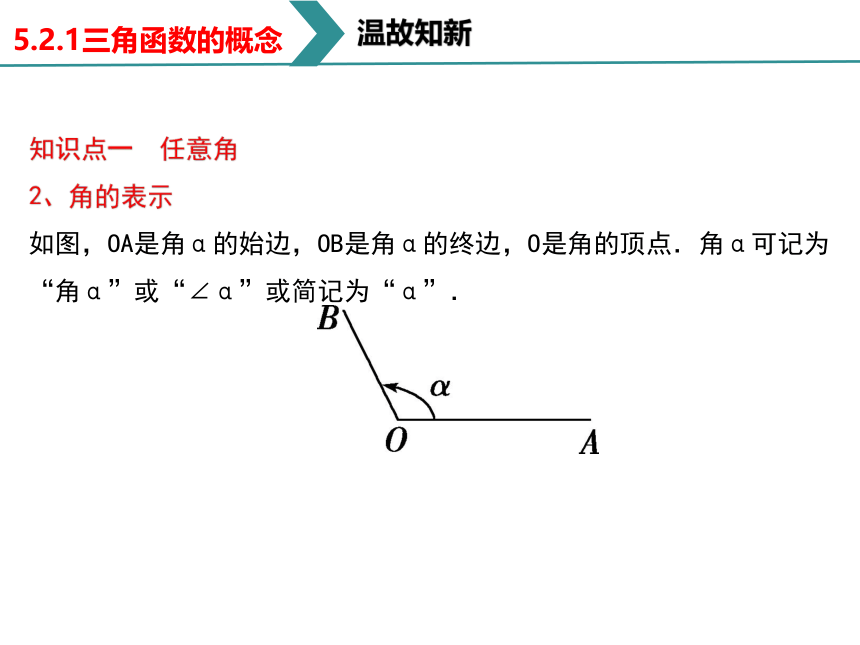
2、角的表示
如图,OA是角α的始边,OB是角α的终边,O是角的顶点.角α可记为“角α”或“∠α”或简记为“α”.
温故知新
知识点一 任意角
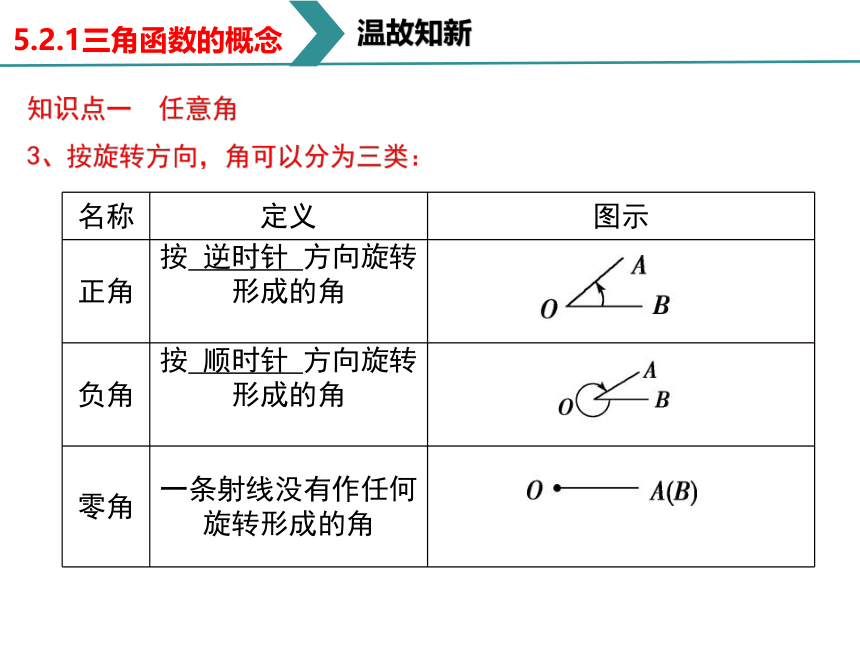
3、按旋转方向,角可以分为三类:
{5940675A-B579-460E-94D1-54222C63F5DA}名称
定义
图示
正角
按 逆时针 方向旋转形成的角
负角
按 顺时针 方向旋转形成的角
零角
一条射线没有作任何旋转形成的角
温故知新
知识点二 象限角
在平面直角坐标系中,若角的顶点与 原点 重合,角的始边与 x轴的非负半轴重合,那么,角的 终边 在第几象限,就说这个角是第几 象限角 ;如果角的终边 在坐标轴 上,就认为这个角不属于任何一个象限.
温故知新
知识点三 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与 整数个周角 的和.
温故知新
知识点三 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与 整数个周角 的和.
情景导入
角α的始边在x轴非负半轴,终边与单位圆交于点P。当 时,点P的坐标是什么?当 时,点P的坐标又是什么?它们唯一确定吗?
问题1
情景导入
一般地,任意给定一个角α,它的终边OP与单位圆交点P的坐标能唯一确定吗?
问题2
答:点P的横、纵坐标都能唯一确定
研探新知
知识点一 任意角的三角函数定义
设α是一个任意角,α∈R,它的终边OP与单位圆相交于点P(x,y).
?
(1)把点P的纵坐标y叫做α的① 正弦函数????,记作sin α,即y=sin α;
(2)把点P的横坐标x叫做α的② 余弦函数????,记作cos α,即x=cos α;
(3)把点P的纵坐标与横坐标的比值?叫做α的③ 正切????,记作tan α,
即? =tanα(x≠0).
研探新知
知识点一 任意角的三角函数定义
由此我们可以推广到一般情况:设α为一个任意角,在α的终边上任取一点P(异于原
点),其坐标为(x,y),且OP=r=?(O为坐标原点),
则sin α=?????????,cos α=?????, tan α= ?????(x≠0)????.
?
研探新知
知识点一 任意角的三角函数定义
正弦函数、余弦函数和正切函数统称为三角函数,记为
正弦函数y=sin x,定义域为????R????;
余弦函数y=cos x,定义域为????R????;
正切函数y=tan x,定义域为?????????.
研探新知
知识点二 正弦、余弦、正切函数值在各象限的符号
研探新知
知识点三 诱导公式1
sin(α+k·2π)=????sin α????,其中k∈Z.
cos(α+k·2π)=cos α,其中k∈Z.
tan(α+k·2π)=????tan α????,其中k∈Z.
研探新知
知识点四 特殊角的三角函数值
典型例题
例1.若α角的终边经过点 ,且 ,则m的值为( ).
C
变式训练
1.若 ,则在角α终边上的点的坐标是( ).
A
变式训练
2.已知角α终边过点P(1,-1),则tanα的值为( )
B
典型例题
例2.“点 在第三象限”是“角为第二象限角”
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件.
c
变式训练
1.若点 在角的终边上,求 的值.
典型例题
例3.计算下列三角比的值
1
变式训练
1.计算
课堂小结
1.任意角的三角函数定义
2.正弦、余弦、正切函数值在各象限的符号
3.诱导公式1
4.特殊角的三角函数值
5.2.1 三角函数的概念
教学目标
1.借助单位圆理解任意角三角函数的定义;
2.根据定义认识函数值的符号,理解诱导公式一;
3.能初步运用定义分析和解决与三角函数值有关的一些简单问题;
4.体验三角函数概念的产生、发展过程,领悟直角坐标系的工具功能,丰富数形结合的经验。
重点难点
重点:
任意角的三角函数(正弦函数、余弦函数、正切函数)的定义;
难点:
任意角的三角函数概念的建构过程。
温故知新
知识点一 任意角
1、角的概念
角可以看成平面内一条 射线 绕着端点从一个位置 旋转 到另一个位置所成的 图形 .
温故知新
知识点一 任意角
2、角的表示
如图,OA是角α的始边,OB是角α的终边,O是角的顶点.角α可记为“角α”或“∠α”或简记为“α”.
温故知新
知识点一 任意角
3、按旋转方向,角可以分为三类:
{5940675A-B579-460E-94D1-54222C63F5DA}名称
定义
图示
正角
按 逆时针 方向旋转形成的角
负角
按 顺时针 方向旋转形成的角
零角
一条射线没有作任何旋转形成的角
温故知新
知识点二 象限角
在平面直角坐标系中,若角的顶点与 原点 重合,角的始边与 x轴的非负半轴重合,那么,角的 终边 在第几象限,就说这个角是第几 象限角 ;如果角的终边 在坐标轴 上,就认为这个角不属于任何一个象限.
温故知新
知识点三 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与 整数个周角 的和.
温故知新
知识点三 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与 整数个周角 的和.
情景导入
角α的始边在x轴非负半轴,终边与单位圆交于点P。当 时,点P的坐标是什么?当 时,点P的坐标又是什么?它们唯一确定吗?
问题1
情景导入
一般地,任意给定一个角α,它的终边OP与单位圆交点P的坐标能唯一确定吗?
问题2
答:点P的横、纵坐标都能唯一确定
研探新知
知识点一 任意角的三角函数定义
设α是一个任意角,α∈R,它的终边OP与单位圆相交于点P(x,y).
?
(1)把点P的纵坐标y叫做α的① 正弦函数????,记作sin α,即y=sin α;
(2)把点P的横坐标x叫做α的② 余弦函数????,记作cos α,即x=cos α;
(3)把点P的纵坐标与横坐标的比值?叫做α的③ 正切????,记作tan α,
即? =tanα(x≠0).
研探新知
知识点一 任意角的三角函数定义
由此我们可以推广到一般情况:设α为一个任意角,在α的终边上任取一点P(异于原
点),其坐标为(x,y),且OP=r=?(O为坐标原点),
则sin α=?????????,cos α=?????, tan α= ?????(x≠0)????.
?
研探新知
知识点一 任意角的三角函数定义
正弦函数、余弦函数和正切函数统称为三角函数,记为
正弦函数y=sin x,定义域为????R????;
余弦函数y=cos x,定义域为????R????;
正切函数y=tan x,定义域为?????????.
研探新知
知识点二 正弦、余弦、正切函数值在各象限的符号
研探新知
知识点三 诱导公式1
sin(α+k·2π)=????sin α????,其中k∈Z.
cos(α+k·2π)=cos α,其中k∈Z.
tan(α+k·2π)=????tan α????,其中k∈Z.
研探新知
知识点四 特殊角的三角函数值
典型例题
例1.若α角的终边经过点 ,且 ,则m的值为( ).
C
变式训练
1.若 ,则在角α终边上的点的坐标是( ).
A
变式训练
2.已知角α终边过点P(1,-1),则tanα的值为( )
B
典型例题
例2.“点 在第三象限”是“角为第二象限角”
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件.
c
变式训练
1.若点 在角的终边上,求 的值.
典型例题
例3.计算下列三角比的值
1
变式训练
1.计算
课堂小结
1.任意角的三角函数定义
2.正弦、余弦、正切函数值在各象限的符号
3.诱导公式1
4.特殊角的三角函数值
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
